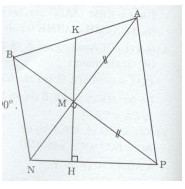
Bài 6 trang 171 Tài liệu dạy – học Toán 7 tập 1

Đề bài

Cho tam giác MNP vuông tại M. Trên tia đối của tia MN ta lấy điểm A sao cho MA = MP, trên tia đối của tia MP ta lấy điểm B sao cho MB = MN.

a) Chứng minh rằng $\Delta MNP = \Delta MBA.$

b) Các tam giác MAP và MBN là tam giác gì ? Vì sao ?

c) Kẻ $MH \bot NP(H \in NP),$  gọi K là giao điểm của đường thẳng MH với AB. Chứng minh rằng K là trung điểm của AB.

Lời giải chi tiết

a)Xét hai tam giác MNP và MBA ta có:

MN = MB (giả thiết)

$\widehat {NMP} = \widehat {BMA}$   (đối đỉnh)

MP = MA (giả thiết)

Do đó: $\Delta MNP = \Delta MBA(c.g.c)$

b) Ta có: $\widehat {NMP} + \widehat {AMP} = {180^0}$   (hai góc kề bù)

Do đó: ${90^0} + \widehat {AMP} = {180^0} \Rightarrow \widehat {AMP} = {180^0} - {90^0} = {90^0}.$

Tam giác MPA vuông tại M có: MA = MP (giả thiết)

Do đó tam giác MPA vuông cân tại M.

Tam giác MNB vuông tại M có: MB = MN (giả thiết)

Do đó: tam giác MNB vuông cân tại M.

c) $\Delta MNP = \Delta MBA$  (chứng minh câu a) $\Rightarrow \widehat {MPN} = \widehat {MAB};\widehat {MNP} = \widehat {MBA}$

Ta có: $\widehat {MNH} + \widehat {NMH} = {90^0}(\Delta MNH$  vuông tại H)

            $\widehat {NMH} + \widehat {HMP} = {90^0}(\Delta MNP$  vuông tại M).

Suy ra $\widehat {MNH} = \widehat {HMP}$

Mà $\widehat {HMP} = \widehat {KMB}$   (đối đỉnh) nên $\widehat {MNH} = \widehat {KMB}.$

Mặt khác $\widehat {KBM} = \widehat {MNH}(cmt)$

Do đó: $\widehat {KBM} = \widehat {KMB} \Rightarrow \Delta KBM$  cân tại K => KB = KM (1).

Ta có: $\widehat {MPH} + \widehat {HMP} = {90^0}(\Delta MHP$  vuông tại H)

            $\widehat {NMH} + \widehat {HMP} = {90^0}(\Delta MNP$  vuông tại M)

$\Rightarrow \widehat {MPH} = \widehat {NMH}$

Mà $\widehat {NMH} = \widehat {KMA}$   (đối đỉnh) nên $\widehat {HPM} = \widehat {KMN}$

Mặt khác $\widehat {KAM} = \widehat {MPH}$   (chứng minh trên)

Do đó: $\widehat {KAM} = \widehat {KMA} \Rightarrow \Delta KAM$  vuông cân tại K => KA = KM (2)

Từ (1) và (2) ta có: KB = KA. Vậy K là trung điểm của AB.

HocTot.XYZ