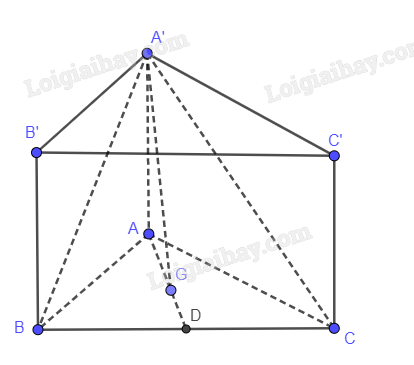
Bài 8.25 trang 79 SGK Toán 11 tập 2 - Cùng khám pháCho hình lăng trụ tam giác ABC.A’B’C’ có ABC là tam giác vuông cân tại A, A’ cách đều A, B, C và AA’ = AB = 2a GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.XYZ và nhận về những phần quà hấp dẫn Đề bài Cho hình lăng trụ tam giác ABC.A’B’C’ có ABC là tam giác vuông cân tại A, A’ cách đều A, B, C và AA’ = AB = 2a. Tính khoảng cách giữa hai đáy của hình lăng trụ. Phương pháp giải - Xem chi tiết Khoảng cách giữa 2 mặt phẳng song song là khoảng cách từ 1 điểm bất kì của mặt này đến mặt phẳng kia. Lời giải chi tiết
Gọi D là trung điểm BC, G là trọng tâm tam giác ABC \(\begin{array}{l}AD = \sqrt 2 a\\ \Rightarrow AG = \frac{{2\sqrt 2 }}{3}a\end{array}\) A’G vuông góc với (ABC) nên A’G vuông góc với AG \(\begin{array}{l}A'G = \sqrt {AA{'^2} - A{G^2}} = \sqrt {4{a^2} - {{\left( {\frac{{2\sqrt 2 }}{3}a} \right)}^2}} = \frac{{2\sqrt 7 }}{3}a\\\end{array}\)  Chia sẻ Bình luận
Tham Gia Group Dành Cho Lớp 11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
