Nội dung từ Loigiaihay.Com
Cho biểu thức \(P = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}} + \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} - \frac{{x - 2\sqrt x }}{{x - 4}}\) và \(Q = \frac{{\sqrt x {\rm{\;}} + 2}}{{\sqrt x {\rm{\;}} - 2}}{\mkern 1mu} {\mkern 1mu} \left( {x \ge 0;x \ne 4} \right)\)
a) Rút gọn P.
b) Tính giá trị của P khi \(x = 16\).
c) Biết \(M = P:Q\). Tìm giá trị của x để \({M^2} < \frac{1}{4}\).
a) Rút gọn phân thức trước rồi rút gọn biểu thức.
b) Thay \(x = 16\) vào P để tính giá trị.
c) Tìm M thay vào \({M^2} < \frac{1}{4}\) để tìm x, lưu ý điều kiện đầu bài.
a) Ta có:
\(P = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}} + \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} - \frac{{x - 2\sqrt x }}{{x - 4}}\)
\(P = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}} + \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} - \frac{{\sqrt x \left( {\sqrt x {\rm{\;}} - 2} \right)}}{{\left( {\sqrt x {\rm{\;}} - 2} \right)\left( {\sqrt x {\rm{\;}} + 2} \right)}}\)
\(P = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}} + \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} - \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}}\)
\(P = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}}\).
b) Thay \(x = 16\) vào P, ta được:
\(P = \frac{{\sqrt {16} }}{{\sqrt {16} - 2}} = \frac{4}{{4 - 2}} = \frac{4}{2} = 2\).
Vậy với \(x = 16\) thì \(P = 2\).
c) Ta có:
\(M = P:Q = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}}:\frac{{\sqrt x {\rm{\;}} + 2}}{{\sqrt x {\rm{\;}} - 2}}{\mkern 1mu} \)
\( = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}}.\frac{{\sqrt x {\rm{\;}} - 2}}{{\sqrt x {\rm{\;}} + 2}} = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}}\)
Vì \({M^2} < \frac{1}{4}\) nên \({\left( {\frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}}} \right)^2} < \frac{1}{4}\). Suy ra \(\left| {\frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}}} \right| < \frac{1}{2}\)
Vì \(\sqrt x > 0\) nên \(\frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} > 0\)
Do đó \(\frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} < \frac{1}{2}\)
\(2\sqrt x {\rm{\;}} < \sqrt x {\rm{\;}} + 2\)
\(\sqrt x {\rm{\;}} < 2\)
\(x < 4\)
Kết hợp điều kiện \(x \ge 0;x \ne 4\) ta được \(0 \le x < 4\).
Vậy để \({M^2} < \frac{1}{4}\) thì \(0 \le x < 4\).

Các bài tập cùng chuyên đề
Bài 1 :
Giá trị của biểu thức \(\sqrt {{{\left( {4 - \sqrt 5 } \right)}^2}} - \sqrt {6 - 2\sqrt 5 } \) là:
-
A.
$5-2\sqrt 5$
-
B.
$4$
-
C.
$2+2\sqrt 5$
-
D.
$1$
Bài 2 :
Rút gọn biểu thức \(5\sqrt a + 2\sqrt {\dfrac{a}{4}} - a\sqrt {\dfrac{4}{a}} - \sqrt {25a} \) với \(a > 0\) ta được
-
A.
$\sqrt a $
-
B.
$4\sqrt a $
-
C.
$2\sqrt a $
-
D.
$ - \sqrt a $
Bài 3 :
Rút gọn biểu thức \(2\sqrt a - \sqrt {9{a^3}} + {a^2}\sqrt {\dfrac{{16}}{a}} + \dfrac{2}{{{a^2}}}\sqrt {36{a^5}} \) với $a > 0$ ta được
-
A.
$14\sqrt a + a\sqrt a $
-
B.
$14\sqrt a - a\sqrt a $
-
C.
$14\sqrt a + 2a\sqrt a $
-
D.
$20\sqrt a - 2a\sqrt a $
Bài 4 :
Đẳng thức nào dưới đây là đúng?
-
A.
$\dfrac{{a - b}}{{{b^2}}}\sqrt {\dfrac{{{a^2}{b^4}}}{{{a^2} - 2ab + {b^2}}}} = a$ với $a - b > 0,b \ne 0$
-
B.
$\dfrac{{a - b}}{{{b^2}}}\sqrt {\dfrac{{{a^2}{b^4}}}{{{a^2} - 2ab + {b^2}}}} = \left| a \right|$ với $a - b > 0,b \ne 0$
-
C.
$\dfrac{{a - b}}{{{b^2}}}\sqrt {\dfrac{{{a^2}{b^4}}}{{{a^2} - 2ab + {b^2}}}} = ab$ với $a - b > 0,b \ne 0$
-
D.
$\dfrac{{a - b}}{{{b^2}}}\sqrt {\dfrac{{{a^2}{b^4}}}{{{a^2} - 2ab + {b^2}}}} = a - b$ với $a - b > 0,b \ne 0$
Bài 5 :
Chọn khẳng định đúng?
-
A.
$\left( {\dfrac{{2\sqrt 3 - \sqrt 6 }}{{\sqrt 8 - 2}} - \dfrac{{\sqrt {216} }}{3}} \right).\left( {\dfrac{{ - a}}{{\sqrt 6 }}} \right) = \dfrac{{ - 3a}}{2}$
-
B.
$\left( {\dfrac{{2\sqrt 3 - \sqrt 6 }}{{\sqrt 8 - 2}} - \dfrac{{\sqrt {216} }}{3}} \right).\left( {\dfrac{{ - a}}{{\sqrt 6 }}} \right) = \dfrac{{3a}}{2}$
-
C.
$\left( {\dfrac{{2\sqrt 3 - \sqrt 6 }}{{\sqrt 8 - 2}} - \dfrac{{\sqrt {216} }}{3}} \right).\left( {\dfrac{{ - a}}{{\sqrt 6 }}} \right) = \dfrac{{ - a}}{2}$
-
D.
$\left( {\dfrac{{2\sqrt 3 - \sqrt 6 }}{{\sqrt 8 - 2}} - \dfrac{{\sqrt {216} }}{3}} \right).\left( {\dfrac{{ - a}}{{\sqrt 6 }}} \right) = \dfrac{a}{2}$
Bài 6 :
Cho $P = \dfrac{2}{{\sqrt x + 1}}$.
Có bao nhiêu giá trị $x \in \mathbb{Z}$ để $P \in \mathbb{Z}$ ?
-
A.
$1$
-
B.
$2$
-
C.
$0$
-
D.
$4$
Bài 7 :
Rút gọn biểu thức \(3\sqrt {8a} + \dfrac{1}{4}\sqrt {\dfrac{{32a}}{{25}}} - \dfrac{a}{{\sqrt 3 }}.\sqrt {\dfrac{3}{{2a}}} - \sqrt {2a} \) với \(a > 0\) ta được:
-
A.
\(\dfrac{{47}}{{10}}\sqrt a \)
-
B.
\(\dfrac{{21}}{5}\sqrt a \)
-
C.
\(\dfrac{{47}}{{10}}\sqrt {2a} \)
-
D.
\(\dfrac{{47}}{5}\sqrt {2a} \)
Bài 8 :
Giá trị của biểu thức \(\sqrt {{{\left( {\sqrt 2 + \sqrt 5 } \right)}^2}} - \sqrt {7 - 2\sqrt {10} } \).
-
A.
\(2\sqrt 2 \)
-
B.
\(0\)
-
C.
\(\sqrt 2 \)
-
D.
\(2\sqrt 5 \)
Bài 9 :
Giá trị của biểu thức \(\sqrt {17 - 12\sqrt 2 } + \sqrt {9 + 4\sqrt 2 } \).
-
A.
\(3 + 4\sqrt 2 \)
-
B.
\(4\)
-
C.
\(2\)
-
D.
\(4\sqrt 2 \)
Bài 10 :
Rút gọn biểu thức \(\left( {\dfrac{1}{2}\sqrt {\dfrac{a}{2}} - \dfrac{3}{2}\sqrt {2a} + \dfrac{4}{5}\sqrt {200a} } \right):\dfrac{1}{8}\) ta được:
-
A.
\(66\sqrt {2a} \)
-
B.
\(52\sqrt {2a} \)
-
C.
\(54\sqrt a \)
-
D.
\(54\sqrt {2a} \)
Bài 11 :
Với \(a,b > 0\), đẳng thức nào dưới đây là đúng?
-
A.
\(\dfrac{{a\sqrt b + b\sqrt a }}{{\sqrt {ab} }} + \dfrac{{a - b}}{{\sqrt a + \sqrt b }} = 2\sqrt a \)
-
B.
\(\dfrac{{a\sqrt b + b\sqrt a }}{{\sqrt {ab} }} + \dfrac{{a - b}}{{\sqrt a + \sqrt b }} = \sqrt a \)
-
C.
\(\dfrac{{a\sqrt b + b\sqrt a }}{{\sqrt {ab} }} + \dfrac{{a - b}}{{\sqrt a + \sqrt b }} = 2\)
-
D.
\(\dfrac{{a\sqrt b + b\sqrt a }}{{\sqrt {ab} }} + \dfrac{{a - b}}{{\sqrt a + \sqrt b }} = 2\sqrt b \)
Bài 12 :
Chọn khẳng định đúng?
-
A.
\(\left( {\dfrac{{\sqrt {14} - \sqrt 7 }}{{1 - \sqrt 2 }} + \dfrac{{\sqrt {15} - \sqrt 5 }}{{1 - \sqrt 3 }}} \right):\dfrac{1}{{a\left( {\sqrt 7 - \sqrt 5 } \right)}} = 2a\)
-
B.
\(\left( {\dfrac{{\sqrt {14} - \sqrt 7 }}{{1 - \sqrt 2 }} + \dfrac{{\sqrt {15} - \sqrt 5 }}{{1 - \sqrt 3 }}} \right):\dfrac{1}{{a\left( {\sqrt 7 - \sqrt 5 } \right)}} = \dfrac{2}{a}\)
-
C.
\(\left( {\dfrac{{\sqrt {14} - \sqrt 7 }}{{1 - \sqrt 2 }} + \dfrac{{\sqrt {15} - \sqrt 5 }}{{1 - \sqrt 3 }}} \right):\dfrac{1}{{a\left( {\sqrt 7 - \sqrt 5 } \right)}} = - 2a\)
-
D.
\(\left( {\dfrac{{\sqrt {14} - \sqrt 7 }}{{1 - \sqrt 2 }} + \dfrac{{\sqrt {15} - \sqrt 5 }}{{1 - \sqrt 3 }}} \right):\dfrac{1}{{a\left( {\sqrt 7 - \sqrt 5 } \right)}} = - \dfrac{a}{2}\)
Bài 13 :
Cho \(P = \dfrac{{\sqrt x + 3}}{{\sqrt x - 2}}\) với \(x \ge 0;x \ne 4\). Có bao nhiêu giá trị \(x \in \mathbb{Z}\) để \(P \in \mathbb{Z}\).
-
A.
\(3\)
-
B.
\(2\)
-
C.
\(0\)
-
D.
\(4\)
Bài 14 :
Rút gọn biểu thức \(A = \sqrt {1 + \dfrac{1}{{{a^2}}} + \dfrac{1}{{{{\left( {a + 1} \right)}^2}}}} \) với \(\left( {a > 0} \right)\)
-
A.
\(A = \dfrac{{{a^2} + a + 1}}{{a\left( {a - 1} \right)}}\)
-
B.
\(A = \dfrac{{{a^2} + a + 1}}{{a\left( {a + 1} \right)}}\)
-
C.
\(A = \dfrac{{{a^2} - a + 1}}{{a\left( {a - 1} \right)}}\)
-
D.
\(A = \dfrac{{{a^2} - a - 1}}{{a\left( {a - 1} \right)}}\)
Bài 15 :
Rút gọn biểu thức: \(T = \dfrac{{\left( {\sqrt {2a} - 2\sqrt 2 } \right)\left( {a - 1} \right)}}{{a - \sqrt a - 2}}\left( {a > 0;a \ne 4} \right)\)
-
A.
\(T = \left( {\sqrt a + 1} \right)\).
-
B.
\(T = \left( {\sqrt a - 1} \right)\).
-
C.
\(T = \sqrt 2 \left( {\sqrt a + 1} \right)\).
-
D.
\(T = \sqrt 2 \left( {\sqrt a - 1} \right)\).
Bài 16 :
Rút gọn biểu thức \(A = \dfrac{{x + \sqrt x + 1}}{{x + \sqrt x - 2}} + \dfrac{1}{{\sqrt x - 1}} + \dfrac{1}{{\sqrt x + 2}}\) với \(x \ge 0,\,\,x \ne 1.\)
-
A.
\(A = \dfrac{{\sqrt x + 1}}{{\sqrt x - 1}}\)
-
B.
\(A = \dfrac{{\sqrt x - 1}}{{\sqrt x + 1}}\)
-
C.
\(A = \dfrac{{\sqrt x + 1}}{{\sqrt x + 2}}\)
-
D.
\(A = \dfrac{{\sqrt x - 1}}{{\sqrt x + 2}}\)
Bài 17 :
Rút gọn các biểu thức sau:
a) \(\sqrt {{{\left( {3 - \sqrt {10} } \right)}^2}} \)
b) \(2\sqrt {{a^2}} + 4a\) với a < 0
c) \(\sqrt {{a^2}} + \sqrt {{{\left( {3 - a} \right)}^2}} \) với 0 < a < 3
Bài 18 :
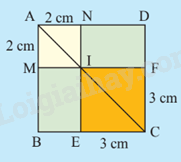
Hình vuông ABCD được chia thành hai hình vuông và hai hình chữ nhật như Hình 3.
a) Tính độ dài đường chéo của hai hình vuông AMIN và CEIF.
b) Tính độ dài đường chéo của hai hình vuông ABCD theo hai cách khác nhau.
Bài 19 :
Rút gọn các biểu thức sau:
a) \(\sqrt {20} - \sqrt 5 \)
b) \(\sqrt {32} - \sqrt {18} + \frac{4}{{\sqrt 2 }}\)
c) \(\left( {2 - \sqrt {10} } \right)\left( {\sqrt 2 - \sqrt 5 } \right)\)
Bài 20 :
Rút gọn các biểu thức sau:
a) \(\frac{2}{3}\sqrt {9{x^3}} + 4x\sqrt {\frac{x}{4}} - {x^2}\sqrt {\frac{1}{x}} \) với x > 0
b) \(\frac{{{a^2} - 5}}{{a + \sqrt {15} }}\) với a \( \ne - \sqrt 5 \)
Bài 21 :
Rút gọn các biểu thức sau:
a) \(2\sqrt 3 - \sqrt {27} \)
b) \(\sqrt {45} - \sqrt {20} + \sqrt 5 \)
c) \(\sqrt {64a} - \sqrt {18} - a\sqrt {\frac{9}{a}} + \sqrt {50} \) với a > 0
Bài 22 :
Tính
a) \(\left( {\sqrt {\frac{4}{3}} + \sqrt 3 } \right)\sqrt 6 \)
b) \(\sqrt {18} :\sqrt 6 + \sqrt 8 .\sqrt {\frac{{27}}{2}} \)
c) \({\left( {1 - 2\sqrt 5 } \right)^2}\)
Bài 23 :
Chứng minh rằng:
a) \(\frac{{a\sqrt b - b\sqrt a }}{{\sqrt {ab} }}:\frac{1}{{\sqrt a + \sqrt b }} = a - b\) với a > 0; b > 0
b) \(\left( {1 + \frac{{a + \sqrt a }}{{\sqrt a + 1}}} \right)\left( {1 - \frac{{a - \sqrt a }}{{\sqrt a - 1}}} \right) = 1 - a\) với a \( \ge \) 0 và a \( \ne \)1
Bài 24 :
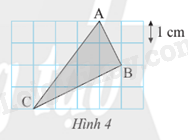
Tam giác ABC được vẽ trên ô vuông như Hình 4. Tính diện tích và chu vi của tam giác ABC
Bài 25 :
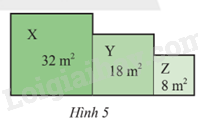
Một vườn hoa gồm ba thửa hình vuông X, Y, Z lần lượt có diện tích như Hình 5. Tính chu vi của vườn hoa đó.
Bài 26 :
Cho a = \(2\sqrt 3 + \sqrt 2 \), b = \(3\sqrt 2 - 2\sqrt 3 \). Rút gọn biểu thức \(\sqrt 3 a - \sqrt 2 b\), ta có kết quả
A. \(3\sqrt 6 \)
B. \( - \sqrt 6 \)
C. \(6\sqrt 3 \)
D. \(12 - \sqrt 6 \)
Bài 27 :
Rút gọn biểu thức \(\frac{1}{{2\sqrt a + \sqrt 2 }} - \frac{1}{{2\sqrt a - \sqrt 2 }}\) với \(a \ge 0\), \(a \ne \frac{1}{2}\), ta có kết quả
A. \(\frac{{\sqrt 2 }}{{1 - 2a}}\)
B. \(\frac{{\sqrt 2 }}{{2a - 1}}\)
C. \(\frac{{\sqrt a }}{{2a - 1}}\)
D. \(\frac{{\sqrt 2 }}{{1 - a}}\)
Bài 28 :
Tính \(\frac{{\sqrt 3 + \sqrt 2 }}{{\sqrt 3 - \sqrt 2 }} - \frac{{\sqrt 3 - \sqrt 2 }}{{\sqrt 3 + \sqrt 2 }}\).
Bài 29 :
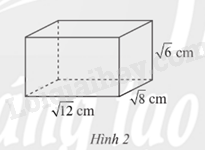
Cho hình hộp chữ nhật có chiều dài \(\sqrt {12} \)cm, chiều rộng\(\sqrt 8 \)cm, chiều cao \(\sqrt 6 \) như Hình 2.
a) Tính thể tích của hình hộp chữ nhật đó.
b) Tính diện tích xung quanh của hình hộp chữ nhật đó.
Bài 30 :
Hãy chép lại và hoàn thành Bảng 3.2. Em có nhận xét gì về giá trị của \(\sqrt {\left( {x + 1} \right)\left( {x + 3} \right)} \) và \(\sqrt {x + 1} .\sqrt {x + 3} \)?













