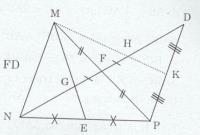
Bài tập 5 trang 127 Tài liệu dạy – học Toán 7 tập 2

Đề bài

Cho tam giác MNP nhọn. Các trung tuyến ME, NF cắt nhau tại G. Trên tia đối của tia FN lấy điểm D sao cho FD  = FN.

a) Chứng minh rằng $\Delta MFN = \Delta PFD$

b) Trên đoạn thẳng FD lấy điểm H sao cho F là trung điểm GH. Gọi K là trung điểm DP. Chứng minh ba điểm M, H, K thẳng hàng.

Lời giải chi tiết

 

a) Xét ∆MFN và ∆PFD có: MF = FP (F là trung điểm của MP)

$\widehat {MFN} = \widehat {PFD}$ (đối đỉnh)

FN = FD (gt)

Do đó: ∆MFN = ∆PFD (c.g.c).

b) ∆MNP có hai đường trung tuyến ME và NF cắt nhau tại G (gt)

=> G là trọng tâm của ∆MNP $\Rightarrow NG = {2 \over 3}NF$

Ta có: NF = FD (gt) và GF = FH (F là trung điểm của GH)

=> NF – GF = FD – FH => NG = HD

Mà $NG = {2 \over 3}NF$ và NF = FD (gt). Nên $HD = {2 \over 3}FD$

∆MDP có DF là đường trung tuyến.

(F là trung điểm của MP) và $HD = {2 \over 3}DF$

Do đó H là trọng tâm của tam giác MDP.

Mà MK là đường trung tuyến của ∆MDP (K là trung điểm của DP)

Nên MK đi qua H => M, H, K thẳng hàng.

HocTot.XYZ