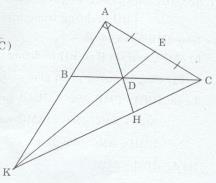
Bài tập 6 trang 127 Tài liệu dạy – học Toán 7 tập 2

Đề bài

Cho tam giác ABC vuông tại A, có $AB = {1 \over 2}AC$ , AD là tia phân giác $\widehat {BAC}\,\,\left( {D \in BC} \right)$, gọi E là trung điểm của AC.

a) Chứng minh rằng DE = DB.

b) AB cắt DE tại K. Chứng minh rằng $\Delta DCK$ cân và B là trung điểm của đoạn thẳng AK.

c) AD cắt CK tại H. Chứng minh rằng $AK \bot KC$

d) Biết AB = 4 cm. Tính DK.

Lời giải chi tiết

 

a) Xét ∆DEA và ∆DBA ta có:

AD là cạnh chung,

$\widehat {DAE} = \widehat {BAD}$ (AD là tia phân giác của $\widehat {BAC}$)

$AE = AB( = {1 \over 2}AC)$

Do đó: ∆DEA = ∆DBA (c.g.c) => DE = DB

b) Ta có: $\widehat {ABD} + \widehat {KBD} = 180^\circ$ (kề bù),

$\widehat {AED} + \widehat {CED} = 180^\circ$ (kề bù)

$\widehat {ABD} = \widehat {AED}$ (∆DBA = ∆DEA)

Do đó $\widehat {KBD} = \widehat {CED}.$

Xét ∆KBD = ∆CED (g.c.g) => KD = CD => Tam giác DCK cân tại D.

Ta có: AB = EC ($= {1 \over 2}AC$)

BK = EC (∆KBD = ∆CED)

Suy ra AB = BK. Vậy B là trung điểm của AK ($B \in AK$).

c) Ta có: $AB = {1 \over 2}AC(gt)$

$AB = {1 \over 2}AK$ (B là trung điểm của AK)

Do đó AC = AK => ∆AKC cân tại A.

Mà AH là đường phân giác của ∆AKC.

Nên AH cũng là đường cao của ∆AKC. Vậy $AH \bot KC.$

d) $AB = {1 \over 2}AC(gt)$

=> AC = 2AB = 2.4 = 8 (cm)

∆ABC vuông tại A có BC² = AB² + AC² (định lí Pythagore)

=> BC² = 4² + 8² = 80 $\Rightarrow BC = 4\sqrt 5 (cm)$

∆AKC có KE là đường trung tuyến (E là trung điểm của AC), CB là đường trung tuyến (B là trung điểm của AK và KE cắt CB tại D)

Nên D là trọng tâm của ∆AKC $\Rightarrow DC = {2 \over 3}BC = {2 \over 3}.4\sqrt 5  = {{8\sqrt 5 } \over 3}(cm)$

Mà DK = DC (câu b). Do đó $DK = {{8\sqrt 5 } \over 3}(cm).$

HocTot.XYZ