Cách chứng minh ba điểm thẳng hàng dựa vào vecto cùng phương trong không gian - Toán 12

Hai vecto được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.

Nếu \(\overrightarrow a \) cùng phương với \(\overrightarrow b \) thì \(\overrightarrow a  = k\overrightarrow b \).

Để chứng minh ba điểm A, B, C bất kì thẳng hàng, ta tìm số thực k khác 0 sao cho \(\overrightarrow {AB}  = k\overrightarrow {AC} \).

Ví dụ minh hoạ:

Cho tam giác ABC, trung tuyến AD. Gọi M là trung điểm của AD, điểm N thuộc AC sao cho \(\overrightarrow {AC}  = 3\overrightarrow {AN} \). Chứng minh B, M, N thẳng hàng.

Giải:

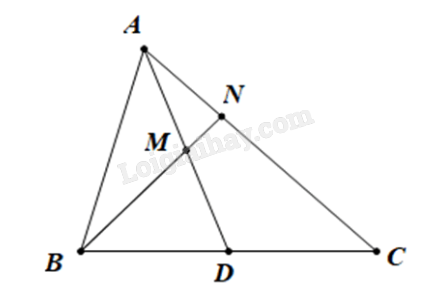
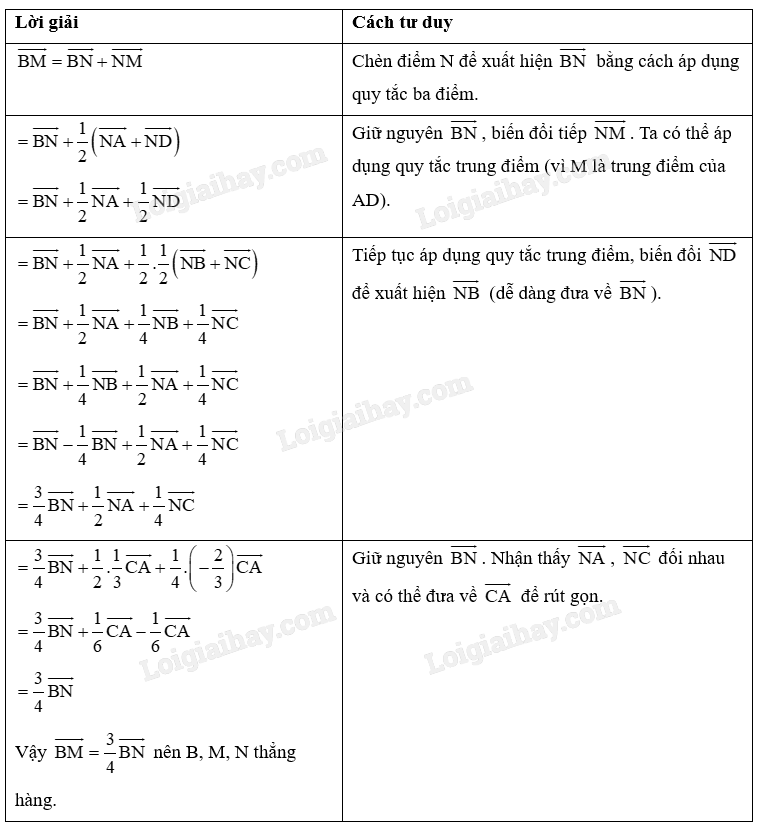
Ta cần chứng minh \(\overrightarrow {BM}  = k\overrightarrow {BN} \), hay biến đổi \(\overrightarrow {BM} \) về \(\overrightarrow {BN} \).