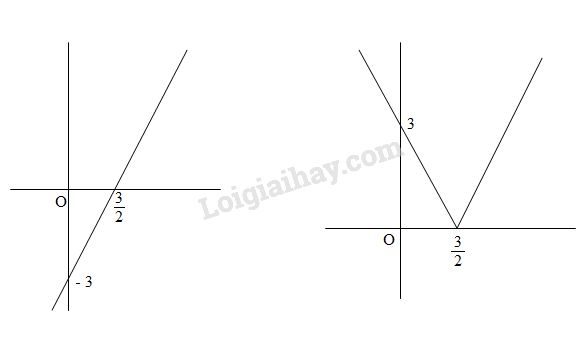
Đề kiểm tra 15 phút - Chương 2 - Đề số 1 - Đại số 10Đáp án và lời giải chi tiết Đề kiểm tra 15 phút - Đề số 4 - Đại số 10 Đề bài Câu 1. Tìm tập xác định của hàm số \(y = \dfrac{{\sqrt {x - 2} }}{{{x^2} - 4x + 3}}\). Câu 2. Xét tính chẵn – lẻ của hàm số \(y = \left| {x - 1} \right| - \left| {x + 1} \right|\). Câu 3. Vẽ đồ thị hàm số \(y=2x-3\). Suy ra đồ thị hàm số \(y = \left| {2x - 3} \right|.\) Lời giải chi tiết Câu 1. Hàm số \(y = \dfrac{{\sqrt {x - 2} }}{{{x^2} - 4x + 3}}\) được xác định khi và chỉ khi \(\left\{ \begin{array}{l}x - 2 \ge 0\\{x^2} - 4x + 3 \ne 0\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\x \ne 1,x \ne 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\x \ne 3\end{array} \right.\) Vậy hàm số có tập xác định \(D = \left[ {2;3} \right) \cup \left( {3; + \infty } \right)\) . Câu 2. Hàm số \(y = \left| {x - 1} \right| - \left| {x + 1} \right|\) có tập xác định \(D = \mathbb{R}\) . Với mọi \(x \in \mathbb{R}\), ta có \( - x \in \mathbb{R}\) \(\begin{array}{l}f( - x) = \left| { - x - 1} \right| - \left| { - x + 1} \right|\\ \;\;\;\;\;\;\;\;\;\;\;= \left| { - \left( {x + 1} \right)} \right| - \left| { - \left( {x - 1} \right)} \right|\\ \;\;\;\;\;\;\;\;\;\;\; = \left| {x + 1} \right| - \left| {x - 1} \right| = - f\left( x \right)\end{array}\) . Vậy hàm số \(y = \left| {x - 1} \right| - \left| {x + 1} \right|\) là hàm số lẻ. Câu 3. Hàm số \(y = 2x – 3\) có đồ thị là một đường thẳng qua hai điểm \(A\left( {\dfrac{3}{2};0} \right)\) và \(B\left( {0; - 3} \right)\). Hàm số \(y = \left| {2x - 3} \right|\) có đồ thị được vẽ theo đồ thị hàm số \(y = 2x – 3\) bằng cách Giữ nguyên phần phía trên trục hoành Lấy đối xứng qua trục hoành phần phía dưới trục hoành.
HocTot.XYZ
|