Đề kiểm tra 15 phút - Chương 2 - Đề số 2 - Đại số 10Đáp án và lời giải chi tiết Đề kiểm tra 15 phút - Đề số 5 - Đại số 10 Đề bài Câu hỏi trắc nghiệm 100% Chọn phương án đúng Câu 1. Tập xác định của hàm số \(y = \dfrac{{2x - {x^2}}}{{{x^2} + 1}}\) là A.\(\mathbb{R}\) B.\(\mathbb{R}\backslash \left\{ { \pm 1} \right\}\) C.\(\mathbb{R}\backslash \left\{ 1 \right\}\) D.\(\mathbb{R}\backslash \left\{ { - 1} \right\}\) Câu 2.Tập xác định của hàm số \(y = \left\{ \begin{array}{l} là A.\(\left[ { - 2;3} \right]\) B. \(\left( { - 2;3} \right)\) C. \(\left[ { - 2;3} \right)\) D.\(\left( { - 2;3} \right]\) Câu 3. Cho hàm số \(f(x) = \left| {2x - 1} \right|\) . Lúc đó \(f\left( x \right) = 3\) khi A. \(x=2\) B. \(x=2\) hoặc \(x=-1\) C. \(x = \pm 2\) D. Kết quả khác Câu 4. Điểm nào sau đây thuộc đồ thị hàm số \(y = \dfrac{{x - 1}}{{2{x^2} - 3x + 1}}\) ? A.\(A\left( {0;1} \right)\) B.\(B\left( {\dfrac{1}{2}; - \dfrac{1}{2}} \right)\) C.\(C\left( {1;0} \right)\) D.\(D\left( {2;\dfrac{1}{3}} \right)\) Câu 5. Cho hàm số \(\;f\left( x \right) = {\rm{ }}2{x^3}\;-{\rm{ }}3x{\rm{ }} + {\rm{ }}1\). Tìm mệnh đề đúng A. \(f\left( x \right)\) là hàm chẵn B. \(f\left( x \right)\) là hàm lẻ C. \(f\left( x \right)\) là hàm không chẵn, không lẻ D. \(f\left( x \right)\) là hàm vừa chẵn, vừa lẻ Câu 6. Trong các hàm số sau, hàm số nào là hàm lẻ ? A. \(y = \left| {x - 2} \right| + \left| {x + 2} \right|\) B. \(y = \left| {x - 2} \right| - \left| {x + 2} \right|\) C. \(y = \left| {1 - 2x} \right| + \left| {1 + 2x} \right|\) D. \(y = \left| {{x^2} - 4} \right|\) Câu 7. Trong các hàm số sau, hàm số nào không phải là hàm chẵn ? A. \(y = - {x^{4\;}}{\rm{ + }}3\) B. \(y = \dfrac{1}{{{x^4}}}\) C. \(y = {x^{4\;}} + 3{x^{2\;}} - 2\) D. \(y = {x^2} - 3x\) Câu 8. Tịnh tiến đồ thị hàm số \(y = 2x{\rm{ }} - 3\) sang phải 2 đơn vị, rồi xuông dưới 1 đơn vị thì đồ thị hàm số A.\(y = 2x + 2\) B. \(y = 2x-6\) C. \(y = 2x-8\) D. \(y = 2x\) Câu 9. Một đường thẳng song song với đường thẳng \(y = - x\sqrt 2 \) là A. \(y + x\sqrt 2 = 2\) B. \(y = - \dfrac{1}{{\sqrt 2 }}x - 2\) C.\(y = x\sqrt 2 + 2\) D.\(y - \dfrac{2}{{\sqrt 2 }}x = - 2\) Câu 10. Đồ thị trên Hình 1 là hàm số
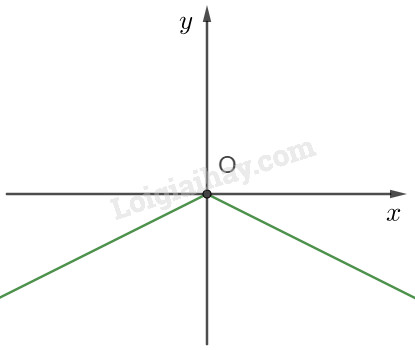
A. \(y = \left| x \right|\) B. \(y = 2\left| x \right| - 2\) C. \(y = \dfrac{1}{2}\left| x \right|\) D. \(y = - \dfrac{1}{2}\left| x \right|\) Lời giải chi tiết Câu 1. Chọn A Do \({x^2} + 1 \ne 0\forall x \in \mathbb{R}\) nên hàm số có tập xác định là \(D = \mathbb{R}\) . Câu 2. Chọn C Tập xác định của hàm số là \(D = \left[ { - 2; - 1} \right) \cup \left[ { - 1;1} \right] \cup \left( {1;3} \right) \)\(\;= \left[ { - 2;3} \right)\) . Câu 3. Chọn B \(\begin{array}{l}f\left( x \right) = 3 \Leftrightarrow \left| {2x - 1} \right| = 3\\{\rm{ }} \Leftrightarrow \left[ \begin{array}{l}2x - 1 = 3\\2x - 1 = - 3\end{array} \right.\\{\rm{ }} \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 1\end{array} \right.\end{array}\) Câu 4. Chọn D Hàm số \(y = \dfrac{{x - 1}}{{2{x^2} - 3x + 1}}\) có tập xác định \(D = \mathbb{R}\backslash \left\{ {1;\dfrac{1}{2}} \right\}\) Gọi (G) là đồ thị hàm số. + \(f\left( 0 \right) = - 1 \ne 1 \Rightarrow A \notin \left( G \right)\) . + \(\dfrac{1}{2} \notin D \Rightarrow B \notin \left( G \right)\). + \(1 \notin \mathbb{R} \Rightarrow C \notin \mathbb{R}\). + \(f\left( 2 \right) = \dfrac{1}{3} \Rightarrow D \in \left( G \right)\). Câu 5. Chọn C Hàm số \(f\left( x \right) = {\rm{ }}2{x^3}\;-{\rm{ }}3x{\rm{ }} + {\rm{ }}1\) có tập xác định \(D = \mathbb{R}\) là tập đối xứng. Ta có \(f\left( 1 \right){\rm{ }} = {\rm{ }}0,{\rm{ }}f\left( { - 1} \right){\rm{ }} = {\rm{ }}2\). Suy ra \(f\left( { - 1} \right) \ne f\left( 1 \right),f\left( { - 1} \right) \ne - f\left( 1 \right)\) . Vậy hàm số không chẵn cũng không lẻ. Câu 6. Chọn B Xét hàm \(f\left( x \right) = \left| {x - 2} \right| - \left| {x + 2} \right|\). Hàm số có tập xác định \(D = \mathbb{R}\) là tập đối xứng. Ta có \(\begin{array}{l}f( - x) = \left| { - x - 2} \right| - \left| { - x + 2} \right|\\{\rm{ }} = \left| { - \left( {x + 2} \right)} \right| - \left| { - \left( {x - 2} \right)} \right|\\{\rm{ }} = \left| {x + 2} \right| - \left| {x - 2} \right| = - f\left( x \right)\end{array}\). Suy ra \(f\left( x \right)\) là hàm số lẻ. Câu 7. Chọn D. Xét hàm số \(f\left( x \right) = {x^2} - 3x\) . Ta có\(f\left( 1 \right) = 2,f\left( { - 1} \right) = 4\) . Suy ra \(f\left( { - 1} \right) \ne f\left( 1 \right)\) . Vậy \(f\left( x \right)\) không phải là hàm chẵn. Câu 8. Chọn C. Khi tịnh tiến đồ thị hàm số y = 2x – 3 sang phải 2 đơn vị, rồi xuống dưới 1 đơn vị thì được đồ thị hàm số \(y = 2\left( {x - 2} \right) - 3 - 1 = 2x - 8\) . Câu 9. Chọn A Ta có \(y + x\sqrt 2 = 2 \Leftrightarrow y = - x\sqrt 2 + 2\) Suy ra đường thẳng này song song với đường thẳng \(y = - x\sqrt 2 \) . Câu 10. Chọn D Chú ý đồ thị hàm số nằm phía dưới trục hoành nên hàm số có giá trị không dương. HocTot.XYZ
|