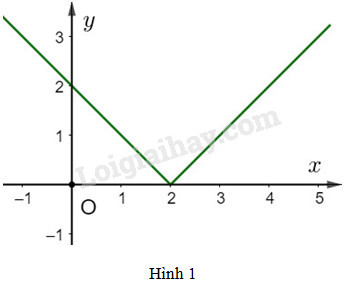
Đề kiểm tra 15 phút - Chương 2 - Đề số 4 - Đại số 10Giải Đề kiểm tra 15 phút - Chương 2 - Đề số 4 - Đại số 10 Đề bài Chọn phương án đúng Câu 1. Tập xác định của hàm số \(y = \sqrt {x - 1} + \dfrac{1}{{x - 3}}\) là A.\(\mathbb{R}\backslash \left\{ 3 \right\}\) B.\(\left[ {1; + \infty } \right)\) C.\(\left[ {1;3} \right) \cup \left( {3; + \infty } \right)\) D.\(\left( {1; + \infty } \right)\backslash \left\{ 3 \right\}\) Câu 2. Tập xác định của hàm số \(y = \dfrac{1}{{\sqrt {\left| {2x - 3} \right|} }}\) là A.\(\mathbb{R}\) B. \(\left( {\dfrac{2}{3}; + \infty } \right)\) C.\(\mathbb{R}\backslash \left\{ {\dfrac{3}{2}} \right\}\) D.\(\left( { - \infty ;\dfrac{3}{2}} \right)\) Câu 3. Cho hàm số \(f(x) = \left| {2x - 3} \right|\) . Lúc đó \(f\left( x \right) = 3\) với A. \(x{\rm{ }} = {\rm{ }}3\) hoặc \(x{\rm{ }} = {\rm{ }}0\) B. \(x{\rm{ }} = {\rm{ }}3\) C. \(x = \pm 3\) D. kết quả khác Câu 4. Điểm nào sau đây thuộc đồ thị hàm số \(y = \dfrac{{x - 2}}{{3{x^2} - 4x + 1}}\) ? A. \(A\left( {\dfrac{1}{3};1} \right)\) B. \(B\left( {\dfrac{1}{2}; 6} \right)\) C. \(D\left( {1;0} \right)\) D. \(D\left( {2;\dfrac{1}{3}} \right)\) Câu 5. Cho hàm số \(f(x) = \dfrac{{3{x^4} + 4{x^2} + 3}}{{{x^2} - 1}}\) . Tìm mệnh đề đúng A. \(f\left( x \right)\) là hàm chẵn B. \(f\left( x \right)\) là hàm lẻ C. \(f\left( x \right)\) là hàm không chẵn, không lẻ D. \(f\left( x \right)\) là hàm vừa chẵn, vừa lẻ Câu 6. Trong các hàm số sau, hàm số nào không phải hàm chẵn ? A. \(y = \left| {x - 2} \right| + \left| {x + 2} \right|\) B. \(y = \left| {3x - 2} \right| - \left| {3x + 2} \right|\) C. \(y = \left| {3 - x} \right| + \left| {3 + x} \right|\) D. \(y = \left| {{x^2} - 4} \right|\) Câu 7. Hàm số nào sau đây đồng biến trên khoảng \(\left( { - 1;0} \right)\) ? A.\(y = \dfrac{7}{x}\) B.\(y = 100x - 200\) C.\(y = 3\left| x \right|\) D. \(y = 2{x^2} - 10\) Câu 8. Tịnh tiến đồ thị hàm số y = 2x – 3 sang trái 2 đơn vị, rồi lên trên 1 đơn vị thì được đồ thị hàm số A. \(y = 2x + 2\) B. \(y = 2x - 6\) C. \(y = 2x - 8\) D. \(y = 2x\) Câu 9. Một đường thẳng song song với đường thẳng \(y = x\sqrt 3 + 2009\) là A. \(y = 1 - x\sqrt 3 x\) B. \(y = \dfrac{1}{{\sqrt 3 }}x - 2\) C. \(y + x\sqrt 3 = 2\) D. \(y - \dfrac{3}{{\sqrt 3 }}x = 4\) Câu 10. Đồ thị hàm số ở hình 1 là của hàm số
A. \(y = \left| x \right| + 2\) B. \(y = \left| {x + 2} \right|\) C. \(y = \left| {2 - x} \right|\) D. Hàm số khác Lời giải chi tiết Câu 1. Chọn C Hàm số \(y = \sqrt {x - 1} + \dfrac{1}{{x - 3}}\) được xác định khi và chỉ khi \(\left\{ \begin{array}{l}x - 1 \ge 0\\x - 3 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\x \ne 3\end{array} \right.\) Vậy tập xác định của hàm số là \(D = \left[ {1;3} \right) \cup \left( {3; + \infty } \right)\) . Câu 2. Chọn C Ta có \(\left| {2x - 3} \right| \ge 0\forall x \in \mathbb{R}\) . Hàm số \(y = \dfrac{1}{{\sqrt {\left| {2x - 3} \right|} }}\) được xác định khi và chỉ khi \(2x - 3 \ne 0 \Leftrightarrow x \ne \dfrac{3}{2}\) . Vậy tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ {\dfrac{3}{2}} \right\}\) . Câu 3. Chọn A Ta có \(f\left( x \right) = 3 \Leftrightarrow \left| {2x - 3} \right| = 3 \). \(\Leftrightarrow \left[ \begin{array}{l}2x - 3 = 3\\2x - 3 = - 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 0\end{array} \right.\) . Câu 4. Chọn B Hàm số \(y = \dfrac{{x - 2}}{{3{x^2} - 4x + 1}}\) được xác định khi và chỉ khi \(3{x^2} - 4x + 1 \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\x \ne \dfrac{1}{3}\end{array} \right.\) Vậy tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ {1;\dfrac{1}{3}} \right\}\) . Gọi (G) là đồ thị của hàm số. \(\dfrac{1}{3} \notin D \Rightarrow A \notin \left( G \right)\). \(f\left( \dfrac{1}{2} \right) = 6 \Rightarrow B \in \left( G \right)\). \(1 \notin D \Rightarrow C \notin \left( G \right)\). \(f\left( 2 \right) = 0 \Rightarrow D \notin \left( G \right)\). Câu 5. Chọn A Hàm số \(f(x) = \dfrac{{3{x^4} + 4{x^2} + 3}}{{{x^2} - 1}}\) có tập xác định \(D = \mathbb{R}\backslash \left\{ { \pm 1} \right\}\) . Với mọi \(x \in D\) ta có: \(x \ne \pm 1 \Rightarrow - x \ne \mp 1 \Rightarrow - x \in D\). \(f\left( { - x} \right) = \dfrac{{3{{\left( -x \right)}^4} - 4{{\left( { - x} \right)}^2} + 3}}{{{{\left( { - x} \right)}^2} - 1}}\)\(\; = \dfrac{{{x^4} - 4{x^2} + 3}}{{{x^2} - 1}} = f\left( x \right) \). Câu 6. Chọn B Hàm số \(y = \left| {3x - 2} \right| - \left| {3x + 2} \right|\) xác định trên \(\mathbb{R}\) .Với mọi \(x \in \mathbb{R}\) ta có \(\begin{array}{l}f\left( { - x} \right) = \left| { - 3x - 2} \right| - \left| { - 3x + 2} \right|\\{\rm{ }} = \left| { - \left( {3x + 2} \right)} \right| - \left| { - \left( {3x - 2} \right)} \right|\\{\rm{ }} = \left| {3x + 2} \right| - \left| {3x - 2} \right| = - f\left( x \right)\end{array}\) Vậy \(f\left( x \right)\) không phải là hàm chẵn. Câu 7. Chọn B Hàm số \(y = \dfrac{7}{x}\) nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\) . Hàm số \(y{\rm{ }} = {\rm{ }}100x{\rm{ }}-{\rm{ }}200\) đồng biến trên \(\mathbb{R}\) nên đồng biến trên khoảng \(\left( { - 1;0} \right)\). Hàm số \(y = 3\left| x \right|\) nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\) Hàm số \(y = 2{x^2}\;-{\rm{ }}10\) nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\) Câu 8. Chọn A Tịnh tiến đồ thị hàm số \(y{\rm{ }} = {\rm{ }}2x{\rm{ }}-{\rm{ }}3\) sang trái 2 đơn vị, rồi lên trên 1 đơn vị thì được đồ thị hàm số \(y = 2\left( {x + 2} \right) - 3 + 1 = 2x + 2\) . Câu 9. Chọn D Ta có \(y - \dfrac{3}{{\sqrt 3 }}x = 4 \Leftrightarrow y = x\sqrt {3}+4 \) . Hàm số này có đồ thị song song với đồ thị hàm số \(y = x\sqrt 3 + 2009\). Câu 10. Chọn C. Đồ thị nằm phía trên trục hoành nên chọn dạng có chứa dấu trị số tuyệt đối. Mặt khác đồ thị có đỉnh là \(\left( {2;0} \right)\) nên chỉ có hàm số \(y = \left| {2 - x} \right|\) là phù hợp. HocTot.XYZ
|