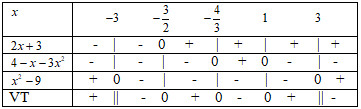
Đề kiểm tra giữa kì 2 Toán 10 - đề số 3 có lời giải chi tiếtĐáp án và lời giải chi tiết Đề kiểm tra giữa kì 2 Toán 10 Đề bài Câu 1. Giải các phương trình sau: a. \(3{{\rm{x}}^2} - 7{\rm{x}} + 4 \le 0\) b. \(\dfrac{{\left( {2{\rm{x}} + 3} \right)\left( {4 - x - 3{{\rm{x}}^2}} \right)}}{{{x^2} - 9}} \ge 0\) c. \(\dfrac{{{x^2} - 4{\rm{x}} + 3}}{{3 - 2{\rm{x}}}} < 1 - x\) d. \(\sqrt {{x^2} - 2{\rm{x}} - 15} \le x - 3\) Câu 2. Tìm tham số m để hàm số sau có tập xác định là tập số thực \(\mathbb{R}\). \(y = \sqrt {\left( {{m^2} + 4} \right){x^2} - 2\left( {2m - 1} \right)x + 4} \) Câu 3. Trong mặt phẳng Oxy, cho tam giác ABC biết phương trình các cạnh là \(\left( {AB} \right):2{\rm{x}} - 3y + 7 = 0;\)\(\left( {BC} \right):2{\rm{x}} - y + 1 = 0;\)\(\left( {AC} \right):x - y + 3 = 0\). a. Tính tọa độ các đỉnh của tam giác. b. Viết phương trình đường cao AK. (K thuộc cạnh BC). c. Tìm tọa độ điểm A’ là điểm đối xứng của điểm A qua đường thẳng BC. d. Tìm tập hợp các điểm cách đều hai cạnh BC và AC. Lời giải chi tiết Câu 1. (VD) Phương pháp: Phân tích thành nhân tử. Sử dụng bảng xét dấu. Giải: a. \(3{{\rm{x}}^2} - 7{\rm{x}} + 4 \le 0\) \(\begin{array}{l} \Leftrightarrow \left( {x - 1} \right)\left( {3{\rm{x}} - 4} \right) \le 0\\ \Leftrightarrow 1 \le x \le \dfrac{4}{3}\end{array}\) b. \(\dfrac{{\left( {2{\rm{x}} + 3} \right)\left( {4 - x - 3{{\rm{x}}^2}} \right)}}{{{x^2} - 9}} \ge 0\) \( \Leftrightarrow \dfrac{{\left( {2{\rm{x}} + 3} \right)\left( {1 - x} \right)\left( {4 + 3{\rm{x}}} \right)}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} \ge 0\) Bảng xét dấu Từ bảng xét dấu ta có: \({\rm{S}} = \left( { - \infty ; - 3} \right) \cup \left[ { - \dfrac{3}{2}; - \dfrac{4}{3}} \right]\cup\left[ {1;3} \right)\) c. \(\dfrac{{{x^2} - 4{\rm{x}} + 3}}{{3 - 2{\rm{x}}}} < 1 - x\) \(\begin{array}{l} \Leftrightarrow \dfrac{{\left( {x - 1} \right)\left( {x - 3} \right)}}{{3 - 2{\rm{x}}}} + \left( {x - 1} \right) < 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {\dfrac{{x - 3}}{{3 - 2{\rm{x}}}} + 1} \right) < 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {\dfrac{{x - 3 + 3 - 2{\rm{x}}}}{{3 - 2{\rm{x}}}}} \right) < 0\\ \Leftrightarrow \left( {x - 1} \right).\dfrac{{ - x}}{{3 - 2{\rm{x}}}} < 0\end{array}\) Từ bảng xét dấu ta có \({\rm{S}} = \left( { - \infty ;0} \right) \cup \left( {1;\dfrac{3}{2}} \right)\) d.\(\sqrt {{x^2} - 2{\rm{x}} - 15} \le x - 3\). Điều kiện \(\left[ \begin{array}{l}{\rm{x}} \ge 5\\x \le - 3\end{array} \right.\) \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x - 3 \ge 0\\{x^2} - 2{\rm{x}} - 15 \le {x^2} - 6{\rm{x}} + 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\4{\rm{x}} \le 24\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\x \le 6\end{array} \right.\end{array}\) Kết hợp với điều kiện xác định ta được \(5 \le x \le 6\). Câu 2. (VD) Phương pháp: \(\sqrt {f\left( x \right)} \) xác định khi \(f\left( x \right) \ge 0\) \(\begin{array}{l}a{x^2} + b{\rm{x}} + c \ge 0\forall x \in \mathbb{R}\\ \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta ' \le 0\end{array} \right.\end{array}\) Giải Hàm số \(y = \sqrt {\left( {{m^2} + 4} \right){x^2} - 2\left( {2m - 1} \right)x + 4} \) xác định trên \(\mathbb{R}\) khi và chỉ khi \(\left( {{m^2} + 4} \right){x^2} - 2\left( {2m - 1} \right)x + 4 \ge 0\)\(\forall x \in \mathbb{R}\) \(\begin{array}{l}\left\{ \begin{array}{l}{m^2} + 4 > 0\\\Delta ' \le 0\end{array} \right.\\ \Leftrightarrow {\left( {2m - 1} \right)^2} - \left( {{m^2} + 4} \right).4 \le 0\\ \Leftrightarrow - 4m + 1 - 16 \le 0\\ \Leftrightarrow m \ge - \dfrac{{15}}{4}\end{array}\) Câu 3. (VD) Phương pháp: a. Tìm giao điểm của các đường thẳng AB, BC, CA. b. Tìm vectơ \(\overrightarrow {BC} \). Đường thẳng AK qua điểm A và nhận \(\overrightarrow {BC} \) làm vectơ pháp tuyến. c. Tìm điểm K và K là trung điểm của AA’. d. Tập hợp các điểm cách đều hai cạnh BC và AC là đường phân giác của góc \(\widehat {ACB}\). Lời giải: a. Tọa độ giao điểm A của AB và AC là nghiệm của hệ phương trình \(\begin{array}{l}\left\{ \begin{array}{l}2{\rm{x}} - 3y + 7 = 0\\x - y + 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 2\\y = 1\end{array} \right.\\ \Rightarrow A\left( { - 2;1} \right)\end{array}\) Điểm B: \(\left\{ \begin{array}{l}2{\rm{x}} - 3y + 7 = 0\\2{\rm{x}} - y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 3\end{array} \right.\) Điểm C: \(\left\{ \begin{array}{l}2{\rm{x}} - y + 1 = 0\\x - y + 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 5\end{array} \right.\) Vậy \(A\left( { - 2;1} \right);B\left( {1;3} \right)C\left( {2;5} \right)\) b. \(\overrightarrow {BC} = \left( {1;2} \right)\) AK qua điểm A và nhận \(\overrightarrow {BC} \) làm vectơ pháp tuyến: \(1\left( {x + 2} \right) + 2\left( {y - 1} \right) = 0\)\( \Leftrightarrow x + 2y = 0\) c. Điểm K là giao của AK và BC nên \(K\left( { - \dfrac{2}{5};\dfrac{1}{5}} \right)\) Điểm A’ đối xứng với A qua BC nên A’ thuộc đường thẳng AK và K là trung điểm của AA’. Ta có \(\left\{ \begin{array}{l}{x_A} + {x_{A'}} = 2{{\rm{x}}_K}\\{y_A} + {y_{A'}} = 2{y_K}\end{array} \right. \Rightarrow A'\left( {\dfrac{{16}}{5}; - \dfrac{8}{5}} \right)\) d. Tập hợp các điểm cách đều hai cạnh BC và AC là đường phân giác của góc \(\widehat {ACB}\). Phương trình đường phân giác của hai đường thẳng BC và AC là \(\dfrac{{2{\rm{x}} - y + 1}}{{\sqrt 5 }} = \pm \dfrac{{x - y + 3}}{{\sqrt 2 }}\) Xét \(\dfrac{{2{\rm{x}} - y + 1}}{{\sqrt 5 }} - \dfrac{{x - y + 3}}{{\sqrt 2 }} = 0\) ta có \(\dfrac{{ - 4}}{{\sqrt 5 }}.\left( { - \dfrac{1}{{\sqrt 2 }}} \right) > 0\) nên A và B cùng phía so với đường thẳng. Vậy đường phân giác của góc \(\widehat {ACB}\) là \(\dfrac{{2{\rm{x}} - y + 1}}{{\sqrt 5 }} + \dfrac{{x - y + 3}}{{\sqrt 2 }} = 0\) HocTot.XYZ
|