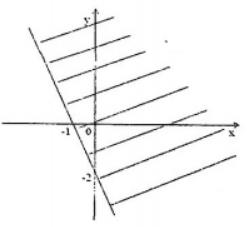
Đề kiểm tra giữa kì 2 Toán 10 - đề số 5 có lời giải chi tiếtĐáp án và lời giải chi tiết Đề kiểm tra giữa kì 2 Toán 10 Đề bài Câu 1. Bất phương trình \(ax + b > 0\) vô nghiệm khi: A. \(\left\{ \begin{array}{l}a = 0\\b \ne 0\end{array} \right.\) B. \(\left\{ \begin{array}{l}a = 0\\b \le 0\end{array} \right.\) C. \(\left\{ \begin{array}{l}a > 0\\b > 0\end{array} \right.\) D. \(\left\{ \begin{array}{l}a \ne 0\\b = 0\end{array} \right.\) Câu 2. Đường thẳng \(\left( d \right)\) có phương trình \(ax + by + c = 0\) với \({a^2} + {b^2} > 0\). Ta xét \(4\) mệnh đề sau:
Số mệnh đề sai trong các mệnh đề trên: A. \(4\) B. \(2\) C. \(1\) D. \(3\) Câu 3. Phương trình tham số của đường thẳng đi qua \(M\left( {3;\,\,4} \right)\) và có véc tơ chỉ phương \(\vec u\left( {1;\,\, - 2} \right)\) là A. \(\left\{ \begin{array}{l}x = 1 + 3t\\y = - 2 + 4t\end{array} \right.\) B. \(\left\{ \begin{array}{l}x = 3 + t\\y = 4 - 2t\end{array} \right.\) C. \(\left\{ \begin{array}{l}x = 3 + 4t\\y = 1 - 2t\end{array} \right.\) D. \(\left\{ \begin{array}{l}x = - 3 + t\\y = - 4 - 2t\end{array} \right.\) Câu 4. Cho bảng xét dấu: Hàm số có bảng xét dấu như trên là: A. \(f\left( x \right) = 16 - 8x\) B. \(f\left( x \right) = x - 2\) C. \(f\left( x \right) = - x - 2\) D. \(f\left( x \right) = 2 - 4x\) Câu 5. Nếu \(a > b > 0,\,\,c > d > 0\) thì bất đẳng thức nào sau đây sai? A. \(ac > bd\) B. \(a - c > b - d\) C. \({a^2} > {b^2}\) D. \(ac > bc\) Câu 6. Tam giác \(ABC\) có \(a = 4,\,\,b = 6,\,\,{m_c} = 4\). Tính độ dài cạnh \(c\). A. \(2\sqrt {10} \) B. \(\dfrac{{\sqrt {10} }}{2}\) C. \(3\sqrt {10} \) D. \(\sqrt {10} \) Câu 7. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right) = \dfrac{{{x^2} + 4x + 5}}{{{x^2} + 3x + 3}}\) lần lượt là \(M\) và \(m\) thì: A. \(M + m = \dfrac{4}{3}\) B. \(M.m = \dfrac{3}{4}\) C. \(\dfrac{M}{m} = \dfrac{4}{3}\) D. \(M - m = \dfrac{4}{3}\) Câu 8. Cho tam thức \(f\left( x \right) = a{x^2} + bx + c\) với \(a < 0\) và \(\Delta = 0\). Phát biểu nào sau đây đúng? A. \(f\left( x \right) < 0,\,\,\forall x \in R\backslash \left\{ { - \dfrac{b}{{2a}}} \right\}\) B. \(f\left( x \right) < 0,\,\,\forall x \in R\) C. \(f\left( x \right) < 0,\,\,\forall x \in R\backslash \left\{ { - \dfrac{b}{a}} \right\}\) D. \(f\left( x \right) < 0\) khi \(x \in \left( { - \dfrac{b}{{2a}};\,\, + \infty } \right)\) và \(f\left( x \right) > 0\) khi \(x \in \left( { - \infty ;\,\, - \dfrac{b}{{2a}}} \right)\) Câu 9. Nếu \(m > 0,\,\,n < 0\) thì bất đẳng thức nào sau đây luôn đúng? A. \( - m > - n\) B. \(mn > 0\) C. \(m > - n\) D. \(n - m < 0\) Câu 10. Góc giữa hai đường thẳng \(\left\{ \begin{array}{l}x = 1 + 2t\\y = - 2 + t\end{array} \right.\) và \(\left\{ \begin{array}{l}x = 1 - 3t\\y = - 2 + t\end{array} \right.\) là: A. \({45^0}\) B. \({30^0}\) C. \({135^0}\) D. \({23^0}13'\) Câu 11. Nếu \(0 < a < 1\) thì bất đẳng thức nào sau đây là đúng? A. \({a^3} > {a^2}\) B. \(a > \dfrac{1}{a}\) C. \(\dfrac{1}{a} > \sqrt a \) D. \(a > \sqrt a \) Câu 12. Tập xác định của hàm số \(y = \sqrt {5 - 4x - {x^2}} \) là A. \(\left( { - \infty ;\,\, - 5} \right] \cup \left[ {1;\,\, + \infty } \right)\) B. \(\left( { - \infty ;\,\, - \dfrac{1}{5}} \right] \cup \left[ {1;\,\, + \infty } \right)\) C. \(\left[ { - 5;\,\,1} \right]\) D. \(\left[ { - \dfrac{1}{5};\,\,1} \right]\) Câu 13. Cho tam giác \(ABC\) có \({b^2} = {a^2} + {c^2} + ac\). Số đo của góc \(B\) là: A. \({150^0}\) B. \({30^0}\) C. \({60^0}\) D. \({120^0}\) Câu 14. Tam giác \(ABC\) có \(AB = 12,\,\,AC = 8\), góc \(A\) bằng \({30^0}\). Tính diện tích tam giác đó. A. \(24\sqrt 2 \) B. \(48\) C. \(24\sqrt 3 \) D. \(24\) Câu 15. Số nghiệm nguyên của bất phương trình \(\dfrac{{{x^4} - {x^2}}}{{{x^2} + 5x + 6}} \le 0\)? A. \(2\) B. \(3\) C. \(1\) D. \(0\) Câu 16. Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nửa mặt phẳng không bị gạch trong hình vẽ bên (kể cả bờ là đường thẳng)? A. \(x + 2y + 2 \le 0\) B. \(2x + y + 2 \le 0\) C. \(2x + y \ge - 2\) D. \(2x + y - 2 \ge 0\) Câu 17. Đường thẳng đi qua hai điểm \(A\left( {3;\,\,4} \right),\,\,B\left( { - 1;\,\,2} \right)\) là: A. \(2x + y - 5 = 0\) B. \(x + 2y - 5 = 0\) C. \(x - 2y + 5 = 0\) D. \(x - 2y - 1 = 0\) Câu 18. Tìm tham số \(m\) để hàm số \(y = \sqrt {\left( {m + 1} \right){x^2} - 2\left( {m + 1} \right) + 4} \) có tập xác định là \(D = \mathbb{R}\)? A. \( - 1 \le m \le 3\) B. \(m \ge - 1\) C. \( - 1 < m < 3\) D. \( - 1 < m \le 3\) Câu 19. Cho hệ bất phương trình \(\left\{ \begin{array}{l}3x - 6 < 0\\mx + m - 1 \ge 0\end{array} \right.\). Giá trị của \(m\) để hệ bất phương trình vô nghiệm là: A. \(0 \le m \le \dfrac{1}{3}\) B. Kết quả khác C. \(m > 0\) D. \(m \le \dfrac{1}{3}\) Câu 20. Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x + 3y - 1 > 0\\5x - y + 4 < 0\end{array} \right.\)? A. \(\left( { - 1;\,\,4} \right)\) B. \(\left( { - 2;\,\,4} \right)\) C. \(\left( {1;\,\,0} \right)\) D. \(\left( { - 3;\,\,4} \right)\) Câu 21. Tổng các nghiệm của bất phương trình \(x\left( {3 - x} \right) \ge x\left( {7 - x} \right) - 6\left( {x - 1} \right)\) trên đoạn \(\left[ { - 6;\,\,6} \right]\). A. \(9\) B. \(18\) C. \(12\) D. \(15\) Câu 22. Phương trình \(2m{x^2} - 2mx + 3 = 0\) vô nghiệm khi và chỉ khi A. \(0 < m < 6\) B. \(\left[ \begin{array}{l}m < 0\\m > 6\end{array} \right.\) C. \(0 \le m \le 3\) D. \(0 \le m < 6\) Câu 23. Tập nghiệm của bất phương trình \(\dfrac{{{x^2} + 2x - 8}}{{\left| {x + 1} \right|}} < 0\) là: A. \(\left( { - 2;\,\, - 1} \right) \cup \left( { - 1;\,\,1} \right)\) B. \(\left( { - 4;\,\, - 1} \right) \cup \left( { - 1;\,\,2} \right)\) C. \(\left( { - 4;\,\, - 1} \right)\) D. \(\left( { - \infty ;\,\, - 4} \right) \cup \left( { - 1;\,\,2} \right)\) Câu 24. Cho tam giác \(ABC\) có \(A\left( { - 1;\,\,6} \right),\,\,B\left( {0;\,\,2} \right),\,\,C\left( {1;\,\,5} \right)\). Gọi \(\alpha \) là góc giữa hai đường cao \(AH\) và \(BK\), khi đó: A. \(\cos \alpha = \dfrac{1}{{\sqrt 2 }}\) B. \(\cos \alpha = \dfrac{7}{{5\sqrt 2 }}\) C. \(\cos \alpha = \dfrac{{ - 1}}{{5\sqrt 2 }}\) D. \(\cos \alpha = \dfrac{1}{{5\sqrt 2 }}\) Câu 25. Cặp bất phương trình nào sau đây không tương đương? A. \({x^2}\left( {x + 2} \right) < 0\) và \(x + 2 < 0\) B. \(2{x^2}\left( {x + 1} \right) \le 0\) và \(x + 1 \le 0\) C. \(\sqrt {x - 1} \ge x\) và \(\left( {2x - 1} \right)\sqrt {x - 1} \ge x\left( {2x - 1} \right)\) D. \(2x + 1 + \dfrac{1}{{x - 2}} < \dfrac{1}{{x - 2}}\)và \(2x + 1 < 0\) Câu 26. Cho hai điểm \(A\left( {1;\,\, - 2} \right),\,\,B\left( {3;\,\,6} \right)\). Phương trình đường trung trực của đoạn thẳng \(AB\) là: A. \(2x + 8y + 5 = 0\) B. \(x + 4y + 10 = 0\) C. \(x + 4y - 10 = 0\) D. \(2x + 8y - 5 = 0\) Câu 27. Số nghiệm nguyên âm của bất phương trình \(\dfrac{{\left| {{x^2} - 8x + 12} \right|}}{{\sqrt {5 - x} }} > \dfrac{{{x^2} - 8x + 12}}{{\sqrt {5 - x} }}\) là A. \(3\) B. vô số C. \(2\) D. \(0\) Câu 28. Tìm tất cả các giá trị thực của tham số \(m\) để bất phương trình \(\left( {{m^2} - 4} \right){x^2} + \left( {m - 2} \right)x + 1 \le 0\) có nghiệm với mọi \(x \in R\). A. Đáp án khác B. \(m \in \left( { - \infty ;\,\,2} \right) \cup \left( {\dfrac{{10}}{3};\,\, + \infty } \right)\) C. \(m \in \left( { - \dfrac{{10}}{3};\,\, - 2} \right)\) D. \(m \in \left( { - \infty ;\,\,2} \right) \cup \left[ {\dfrac{{10}}{3};\,\, + \infty } \right)\) Câu 29. Tìm tất cả các gía trị thực của tham số \(m\) sao cho phương trình \(\left( {m - 1} \right){x^2} - 2\left( {m + 1} \right)x + m + 4 = 0\) có hai nghiệm dương phân biệt. A. \(m < - 4\) hoặc \(1 < m < 5\) B. \(m < - 1\) hoặc \( - 4 < m < 5\) C. \(1 < m < 5\) D. \( - 4 < m < 5\) Câu 30. Tập hợp các giá trị của \(m\) để \(3\) đường thẳng sau đồng quy: \(2x - y + 1 = 0\), \(x - y + 2 = 0\), \(\left( {1 + {m^2}} \right)x - y + 2m - 1 = 0\) là A. \(\left\{ {1;\,\, - 3} \right\}\) B. \(\left\{ 1 \right\}\) C. \(\left\{ { - 3} \right\}\) D. Đáp án khác
Lời giải chi tiết
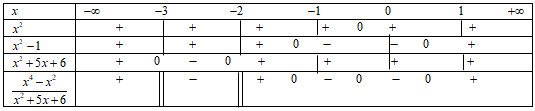
Câu 1 (TH) - Bất phương trình Phương pháp: Sử dụng phương pháp biện luận bất phương trình bậc nhất một ẩn. Cách giải: Nếu \(a = 0\) và \(b \le 0\) thì bất phương trình vô nghiệm. Chọn B. Câu 2 (TH) - Phương trình đường thẳng Phương pháp: Xác định VTCP, VTPT, hệ só góc của đường thẳng \(d\). Cách giải: Đường thẳng \(\left( d \right)\) có phương trình \(ax + by + c = 0\) với \({a^2} + {b^2} > 0\), ta có: +) VTPT \({\vec n_d} = \left( {a;\,\,b} \right) \Rightarrow \vec u = \left( {b;\,\, - a} \right)\,\) là VTCP của \(\left( d \right)\) \( \Rightarrow \) Mệnh đề \(1\) đúng +) Nếu \(b = 0\) đường thẳng \(\left( d \right)\) trở thành \(ax + c = 0 \Rightarrow x = - \dfrac{c}{a}\) \( \Rightarrow \) \(x = - \dfrac{c}{a}\) là đường thẳng song song hoặc trùng với trục tung. \( \Rightarrow \) Mệnh đề \(2\) sai +) VTPT \({\vec n_d} = \left( {a;\,\,b} \right)\)\( \Rightarrow k{\vec n_d} = \left( {ka;\,\,kb} \right)\,,\)\(\forall k \ne 0\)cũng là VTPT của \(\left( d \right)\) \( \Rightarrow \) Mệnh đề \(3\) sai +) Nếu \(b \ne 0\) ta có: \(ax + by + c = 0\)\( \Rightarrow y = - \dfrac{a}{b}x - \dfrac{c}{b}\) \( \Rightarrow \) Đường thẳng \(\left( d \right)\) có hệ số góc là \(k - \dfrac{a}{b}\). \( \Rightarrow \) Mệnh đề \(4\) đúng Vậy có \(2\) mệnh đề sai. Chọn B. Câu 3 (TH) - Phương trình đường thẳng Phương pháp: Phương trình tham số của đường thẳng \(\Delta \) đi qua \(M\left( {{x_0};\,\,{y_0}} \right)\) nhận \(\vec u = \left( {a;\,\,b} \right)\) là VTCP có dạng \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\,\,\left( {t \in \mathbb{R}} \right)\) Cách giải: Phương trình tham số đường thẳng đi qua \(M\left( {3;\,\,4} \right)\) và có véc tơ chỉ phương \(\vec u\left( {1;\,\, - 2} \right)\) là \(\left\{ \begin{array}{l}x = 3 + t\\y = 4 - 2t\end{array} \right.\) Chọn B. Câu 4 (TH) - Dấu của nhị thức bậc nhất Phương pháp: Hàm số \(f\left( x \right) = ax + b\) có giá trị cùng dấu với hệ số \(a\) khi \(x\) lấy giá trị trong khoảng \(\left( { - \dfrac{b}{a};\,\, + \infty } \right)\), trái dấu với hệ số \(a\) khi \(x\) lấy giá trị trong khoảng \(\left( { - \infty ;\,\, - \dfrac{b}{a}} \right)\). Cách giải: Đặt \(f\left( x \right) = ax + b\) là hàm số cần tìm. Quan sát bảng xét dấu ta thấy, hàm số có nghiệm là \(x = 2\). \( \Rightarrow \) Đáp án C và đáp án D sai. Trong khoảng \(\left( {2;\,\, + \infty } \right)\), hàm số \(f\left( x \right) = ax + b\) mang dấu \( - \) nên \(a < 0\). \( \Rightarrow \) Đáp án A đúng và đáp án B sai. Chọn A. Câu 5 (TH) - Bất đẳng thức Phương pháp: Sử dụng các tính chất cơ bản của bất đẳng thức để chứng minh. Cách giải: +) \(\left\{ \begin{array}{l}a > b > 0\\c > d > 0\end{array} \right.\) \( \Rightarrow ac > bd\) \( \Rightarrow \) Đáp án A đúng. +) Chọn \(a = 5,\,\,b = 4,\,\,c = 3,\,\,d = 1\) thỏa mãn \(a > b > 0,\,\,c > d > 0\). \(\left\{ \begin{array}{l}5 > 4 > 0\\3 > 1 > 0\end{array} \right.\)\( \Rightarrow 5 - 3 > 4 - 1\) (vô lý) \( \Rightarrow \) Đáp án B sai. +) \(a > b > 0 \Rightarrow {a^2} > {b^2}\) (vì hai vế của bất đẳng thức luôn dương nên khi bình phương hai vế thì dấu của bất đẳng thức không đổi chiều) \( \Rightarrow \) Đáp án C đúng. +) \(\left\{ \begin{array}{l}a > b > 0\\c > 0\end{array} \right.\)\( \Rightarrow ac > bc\) (nhân cả hai vế của bất đẳng thức \(a > b\) với một số \(c > 0\) thì dấu của BĐT không đổi chiều) \( \Rightarrow \) Đáp án D đúng. Chọn B. Câu 6 (TH) - Các hệ thức lượng trong tam giác và giải tam giác Phương pháp: Sử dụng công thức tính độ dài đường trung tuyến trong tam giác: \(m_c^2 = \dfrac{{{a^2} + {b^2}}}{2} - \dfrac{{{c^2}}}{4}\) Cách giải: Áp dụng công thức tính độ dài đường trung tuyến của tam giác \(ABC\) ta có: \(m_c^2 = \dfrac{{{a^2} + {b^2}}}{2} - \dfrac{{{c^2}}}{4}\) \(\begin{array}{l} \Leftrightarrow 4m_c^2 = 2\left( {{a^2} + {b^2}} \right) - {c^2}\\ \Leftrightarrow {c^2} = 2\left( {{a^2} + {b^2}} \right) - 4m_c^2\end{array}\) Mà \(a = 4,\,\,b = 6,\,\,{m_c} = 4\) nên ta có: \({c^2} = 2\left( {{4^2} + {6^2}} \right) - {4.4^2} = 40\) \( \Rightarrow c = \sqrt {40} = 2\sqrt {10} \) Chọn A. Câu 7 (TH) - Phương trình quy về phương trình bậc hai Phương pháp: Đặt: \(\dfrac{{{x^2} + 4x + 5}}{{{x^2} + 3x + 3}} = A\) \(\left( 1 \right)\) Biến đổi \(\left( 1 \right)\)về dạng phương trình bậc hai và tìm điều kiện để \(\left( 1 \right)\) có nghiệm. Từ đó tìm được \(M\) và \(m\). Cách giải: Đặt \(f\left( x \right) = \dfrac{{{x^2} + 4x + 5}}{{{x^2} + 3x + 3}} = A\) \(\begin{array}{l} \Leftrightarrow {x^2} + 4x + 5 = A\left( {{x^2} + 3x + 3} \right)\\ \Leftrightarrow {x^2} + 4x + 5 - A\left( {{x^2} + 3x + 3} \right) = 0\\ \Leftrightarrow {x^2} + 4x + 5 - A{x^2} - 3Ax - 3A = 0\\ \Leftrightarrow \left( {1 - A} \right){x^2} + \left( {4 - 3A} \right)x + 5 - 3A = 0\,\,\,\,\left( 1 \right)\end{array}\) Phương trình \(\left( 1 \right)\) có nghiệm \( \Leftrightarrow \Delta \ge 0\) \(\begin{array}{l}\Delta \ge 0 \Leftrightarrow {\left( {4 - 3A} \right)^2} \\- 4.\left( {1 - A} \right)\left( {5 - 3A} \right) \ge 0\\\, \Leftrightarrow \left( {16 - 24A + 9{A^2}} \right)\\ - \left( {4 - 4A} \right)\left( {5 - 3A} \right) \ge 0\\\, \Leftrightarrow \left( {16 - 24A + 9{A^2}} \right)\\ - \left( {20 - 12A - 20A + 12{A^2}} \right) \ge 0\\\, \Leftrightarrow 16 - 24A + 9{A^2} - 20 \\+ 12A + 20A - 12{A^2} \ge 0\\\, \Leftrightarrow - 3{A^2} + 8A - 4 \ge 0\\\, \Leftrightarrow 3{A^2} - 8A + 4 \le 0\\\, \Leftrightarrow \left( {A - 2} \right)\left( {3A - 2} \right) \le 0\\ \Leftrightarrow \dfrac{2}{3} \le A \le 2\end{array}\) +) \(A \ge \dfrac{2}{3} \Rightarrow Min\,A = \dfrac{2}{3}\) \(A = \dfrac{2}{3} \Leftrightarrow \dfrac{{{x^2} + 4x + 5}}{{{x^2} + 3x + 3}} = \dfrac{2}{3}\)\( \Leftrightarrow 3{x^2} + 12x + 15 = 2{x^2} + 6x + 6\)\( \Leftrightarrow {x^2} + 6x + 9 = 0\)\( \Leftrightarrow x = - 3\) +) \(A \le 2 \Rightarrow Max\,A = 2\) \(A = 2 \Leftrightarrow \dfrac{{{x^2} + 4x + 5}}{{{x^2} + 3x + 3}} = 2\)\( \Leftrightarrow {x^2} + 4x + 5 = 2{x^2} + 6x + 6\)\( \Leftrightarrow {x^2} + 2x + 1 = 0\)\( \Leftrightarrow x = - 1\) Vậy \(Min\,f\left( x \right) = Min\,A = \dfrac{2}{3} \Leftrightarrow x = - 1\); \(Max\,f\left( x \right) = Max\,A = 2 \Leftrightarrow x = - 1\) Khi đó, ta có: \(\left\{ \begin{array}{l}M = 2\\m = \dfrac{2}{3}\end{array} \right.\) \(M + m = \dfrac{8}{3}\)\( \Rightarrow \) Đáp án \(A\) sai. \(Mm = \dfrac{4}{3}\)\( \Rightarrow \) Đáp án \(B\) sai. \(\dfrac{M}{m} = 3\)\( \Rightarrow \) Đáp án \(C\) sai. \(M - m = \dfrac{4}{3}\)\( \Rightarrow \) Đáp án\(D\) đúng. Chọn D. Câu 8 (TH) - Dấu của tam thức bậc hai Phương pháp: Sử dụng phương pháp biện luận phương trình bậc hai (Nếu \(\Delta = 0\) thì \(f\left( x \right)\) có nghiệm kép). Đưa \(f\left( x \right)\) về dạng \(f\left( x \right) = a{M^2}\left( x \right)\) để xét dấu của \(f\left( x \right)\). Cách giải: Vì \(\Delta = 0\) nên \(f\left( x \right)\) có nghiệm kép \(x = - \dfrac{b}{{2a}}\). \( \Rightarrow f\left( x \right) = a{\left( {x + \dfrac{b}{{2a}}} \right)^2}\) mà \(a < 0\) nên \(f\left( x \right) = a{\left( {x + \dfrac{b}{{2a}}} \right)^2} \le 0\) Dấu “\( = \)” xảy ra \( \Leftrightarrow x = - \dfrac{b}{{2a}}\). Do đó, \(f\left( x \right) < 0,\,\,\forall x \in R\backslash \left\{ { - \dfrac{b}{{2a}}} \right\}\) Chọn A. Câu 9 (TH) - Bất đẳng thức Phương pháp: Sử dụng các tính chất cơ bản của bất đẳng thức để chứng minh. Cách giải: Nếu \(m > 0,\,\,n < 0\) thì \(m > n\). +) Xét đáp án A: \( - m > - n \Leftrightarrow m < n\) (trái với đề bài) \( \Rightarrow \) Đáp án \(A\)sai. +) Xét đáp án B: \(mn > 0 \Rightarrow \)\(m\) và \(n\) cùng dấu (trái với đề bài) \( \Rightarrow \) Đáp án \(B\) sai. +) Xét đáp án C: Chọn \(m = 3 > 0,\,\,n = - 4 < 0 \Rightarrow 3 > - \left( { - 4} \right)\) hay \(3 > 4\) (vô lý) \( \Rightarrow \) Đáp án \(C\) sai. +) Xét đáp án D: \(n - m < 0 \Leftrightarrow m > n\) (thỏa mãn đề bài) \( \Rightarrow \) Đáp án \(D\) đúng. Chọn D. Câu 10 (TH) - Tích vô hướng của hai vectơ Phương pháp: Công thức tính góc giữa hai đường thẳng: \(\cos \varphi = \left| {\cos \left( {{{\vec n}_1},\,\,{{\vec n}_2}} \right)} \right| = \dfrac{{\left| {{{\vec n}_1}.\,{{\vec n}_2}} \right|}}{{\left| {{{\vec n}_1}} \right|.\left| {{{\vec n}_2}} \right|}}\) hoặc \(\cos \varphi = \left| {\cos \left( {{{\vec u}_1},\,\,{{\vec u}_2}} \right)} \right| = \dfrac{{\left| {{{\vec u}_1}.\,{{\vec u}_2}} \right|}}{{\left| {{{\vec u}_1}} \right|.\left| {{{\vec u}_2}} \right|}}\) Cách giải: \(\left( {{d_1}} \right):\,\,\left\{ \begin{array}{l}x = 1 + 2t\\y = - 2 + t\end{array} \right. \Rightarrow {\vec u_{{d_1}}} = \left( {2;\,\,1} \right)\) \(\left( {{d_2}} \right):\,\,\left\{ \begin{array}{l}x = 1 - 3t\\y = - 2 + t\end{array} \right. \Rightarrow {\vec u_{{d_2}}} = \left( { - 3;\,\,1} \right)\) \({\rm{cos}}\left( {{d_1},{d_2}} \right) = {\rm{cos}}\left( {{{\vec u}_{{d_1}}},{{\vec u}_{{d_2}}}} \right)\)\( = \dfrac{{\left| {{{\vec u}_{{d_1}}}.{{\vec u}_{{d_2}}}} \right|}}{{\left| {{{\vec u}_{{d_1}}}} \right|.\left| {{{\vec u}_{{d_2}}}} \right|}}\)\( = \dfrac{{\left| {2.\left( { - 3} \right) + 1.1} \right|}}{{\sqrt {{2^2} + {1^2}} .\sqrt {{{\left( { - 3} \right)}^2} + {1^2}} }}\)\( = \dfrac{5}{{\sqrt 5 .\sqrt {10} }} = \dfrac{1}{{\sqrt 2 }}\) \( \Rightarrow \left( {{d_1},\,\,{d_2}} \right) = {45^0}\) Vậy góc giữa hai đường thẳng trên bằng \({45^0}\). Chọn A. Câu 11 (TH) - Bất đẳng thức Phương pháp: Sử dụng các tính chất cơ bản của bất đẳng thức để chứn minh. Cách giải: +) Xét đáp án A: \({a^3} > {a^2} \Leftrightarrow {a^3} - {a^2} > 0\\ \Leftrightarrow {a^2}\left( {a - 1} \right) > 0 \Leftrightarrow \left\{ \begin{array}{l}{a^2} > 0\\a - 1 > 0\end{array} \right.\\ \Leftrightarrow a > 1\) (trái với đề bài) \( \Rightarrow \) Đáp án \(A\)sai. +) Xét đáp án B: \(a > \dfrac{1}{a}\)\( \Leftrightarrow \dfrac{{{a^2} - 1}}{a} > 0\) \( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{a^2} - 1 > 0\\a > 0\end{array} \right.\\\left\{ \begin{array}{l}{a^2} - 1 < 0\\a < 0\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}\left[ \begin{array}{l}a > 1\\a < - 1\end{array} \right.\\a > 0\end{array} \right.\\\left\{ \begin{array}{l} - 1 < a < 1\\a < 0\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}a > 1\\ - 1 < a < 0\end{array} \right.\) (trái với đề bài) \( \Rightarrow \) Đáp án \(B\)sai. +) Xét đáp án C: \(\dfrac{1}{a} > \sqrt a \) \( \Leftrightarrow \dfrac{{1 - a\sqrt a }}{a} > 0\)\( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\a\sqrt a < 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\{\left( {a\sqrt a } \right)^2} < {1^2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\{a^3} < 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a > 0\\a < 1\end{array} \right.\)\( \Leftrightarrow 0 < a < 1\) (thỏa mãn đề bài) \( \Rightarrow \) Đáp án \(C\) đúng. +) Xét đáp án D: \(a > \sqrt a \Leftrightarrow \left\{ \begin{array}{l}a \ge 0\\{a^2} > a\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a \ge 0\\a\left( {a - 1} \right) > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a \ge 0\\\left[ \begin{array}{l}\left\{ \begin{array}{l}a > 0\\a > 1\end{array} \right.\\\left\{ \begin{array}{l}a < 0\\a < 1\end{array} \right.\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a \ge 0\\\left[ \begin{array}{l}a > 1\\a < 0\end{array} \right.\end{array} \right.\)\( \Leftrightarrow a > 1\) (trái với đề bài) \( \Rightarrow \) Đáp án \(D\) sai. Chọn C. Câu 12 (TH) - Tập xác định của hàm số Phương pháp: Hàm số \(y = \sqrt {f\left( x \right)} \) xác định khi và chỉ khi \(f\left( x \right) \ge 0\). Cách giải: Hàm số \(y = \sqrt {5 - 4x - {x^2}} \) xác định khi và chỉ khi \(5 - 4x - {x^2} \ge 0\). Ta có bảng xét dấu: Vậy tập xác định của hàm số \(y = \sqrt {5 - 4x - {x^2}} \) là \(\left[ { - 5;\,\,1} \right]\). Chọn C. Câu 13 (TH) - Các hệ thức lượng trong tam giác và giải tam giác Phương pháp: Sử dụng hệ quả của định lý cô-sin trong tam giác: \(\cos B = \dfrac{{{c^2} + {a^2} - {b^2}}}{{2ac}}\) Cách giải: Theo đề bài, ta có: \({b^2} = {a^2} + {c^2} + ac\) \( \Rightarrow {b^2} = {a^2} + {c^2} - 2.\left( { - \dfrac{1}{2}} \right).ac\)\( \Rightarrow - \dfrac{1}{2} = \dfrac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\) Mà \(\cos B = \dfrac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\)\( \Rightarrow \cos B = - \dfrac{1}{2}\)\( \Rightarrow \angle B = {120^0}\). Chọn D. Câu 14 (TH) - Các hệ thức lượng trong tam giác và giải tam giác Phương pháp: Sử dụng công thức: \(S = \dfrac{1}{2}ab\sin C\)\( = \dfrac{1}{2}bc\sin A\)\( = \dfrac{1}{2}ca\sin B\) Cách giải: Áp dụng công thức tính diện tích, ta có: \({S_{\Delta ABC}} = \dfrac{1}{2}.AB.AC.\sin A\)\( = \dfrac{1}{2}.12.8.\sin {30^0} = 24\) Chọn D. Câu 15 (TH) - Bất phương trình Phương pháp: Giải bất phương trình để tìm tập nghiệm và tìm các giá trị nguyên nằm trong tập nghiệm đó. Cách giải: ĐKXĐ: \({x^2} + 5x + 6 \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne - 2\\x \ne - 3\end{array} \right.\) \(\dfrac{{{x^4} - {x^2}}}{{{x^2} + 5x + 6}} \le 0 \Leftrightarrow \dfrac{{{x^2}\left( {{x^2} - 1} \right)}}{{{x^2} + 5x + 6}} \le 0\) Ta có bảng xét dấu:
\( \Rightarrow x \in \left( { - 3;\,\, - 2} \right) \cup \left[ { - 1;\,\,1} \right]\) Mà \(x \in \mathbb{Z}\) nên \(x \in \left\{ { - 1;\,\,0;\,\,1} \right\}\). Vậy phương trình có \(3\) nghiệm nguyên. Chọn B. Câu 16 (TH) - Phương trình đường thẳng Phương pháp: Viết phương trình đường thẳng đi qua hai điểm \(\left( { - 1;\,\,0} \right)\) và \(\left( {0;\,\, - 2} \right)\). Từ đó, dựa vào đồ thị để kết luận bất phương trình. Cách giải: Đường thẳng đi qua hai điểm \(\left( { - 1;\,\,0} \right)\) và \(\left( {0;\,\, - 2} \right)\) \( \Rightarrow VTCP\,{\mathop u\limits^ \to _d} = \left( {1; - 2} \right)\) \( \Rightarrow VTPT\,\,{\vec n_d} = \left( {2;\,\,1} \right)\) \( \Rightarrow \,\,\)Miền nghiệm không bị gạch biểu diễn BPT \(2x + y + 2 \le 0\) Chọn B. Câu 17 (TH) - Phương trình đường thẳng Phương pháp: Tìm VTCP và suy ra VTPT của \(AB\). Phương trình đường thẳng \(AB\) đi qua \(A\left( {{x_0};\,\,{y_0}} \right)\), nhận \(\vec n = \left( {a;\,\,b} \right)\) có dạng: \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\) Cách giải: \(A\left( {3;\,\,4} \right),\,\,B\left( { - 1;\,\,2} \right)\)\( \Rightarrow \overrightarrow {AB} = \left( { - 4;\, - 2} \right) = \left( {2;1} \right)\)\( \Rightarrow {\vec n_{AB}} = \left( {1;\,\, - 2} \right)\) Phương trình đường thẳng \(AB\) đi qua \(A\left( {3;\,\,4} \right)\) có VTPT \({\vec n_{AB}} = \left( {1;\,\, - 2} \right)\) là : \(\begin{array}{l}1.\left( {x - 3} \right) - 2.\left( {y - 4} \right) = 0\\ \Leftrightarrow x - 3 - 2y + 8 = 0\\ \Leftrightarrow x - 2y + 5 = 0\end{array}\) Chọn C. Câu 18 (TH) - Tập xác định của hàm số Phương pháp: Hàm số \(y = \sqrt {f\left( x \right)} \) có tập xác định là \(D = R\) khi và chỉ khi \(f\left( x \right) \ge 0\) với \(\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta \le 0\end{array} \right.\). Cách giải: Hàm số \(y = \sqrt {\left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 4} \) có tập xác định là \(D = \mathbb{R}\) khi và chỉ khi \(\left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 4 \ge 0\) với mọi \(x \in \mathbb{R}\). \(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}a > 0\\\Delta \le 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m + 1 > 0\\4{\left( {m + 1} \right)^2} - 16\left( {m + 1} \right) \le 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m > - 1\\4{m^2} - 8m - 12 \le 0\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}m > - 1\\ - 1 \le m \le 3\end{array} \right.\\ \Leftrightarrow - 1 < m \le 3\end{array}\) Chọn D. Câu 19 (TH) - Bất phương trình và hệ bất phương trình một ẩn Phương pháp: Sử dụng phương pháp giải và biện luận bất phương trình. Cách giải: \(\left\{ \begin{array}{l}3x - 6 < 0\\mx + m - 1 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < 2\\mx \ge 1 - m\end{array} \right.\) TH1: \(m = 0\) Hệ bất phương trình trở thành \(\left\{ \begin{array}{l}x < 0\\0 \ge 1\end{array} \right.\) (vô lý) \( \Rightarrow \) Hệ bất phương trình vô nghiệm với \(m = 0\) TH2: \(m \ne 0\) Hệ bất phương trình trở thành \(\left\{ \begin{array}{l}x < 2\\mx \ge 1 - m\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x < 2\\x \ge \dfrac{{1 - m}}{m}\end{array} \right.\) Hệ bất phương trình vô nghiệm \( \Leftrightarrow \dfrac{{1 - m}}{m} \ge 2\)\( \Leftrightarrow \dfrac{{1 - 3m}}{m} \ge 0\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}1 - 3m \ge 0\\m > 0\end{array} \right.\\\left\{ \begin{array}{l}1 - 3m \le 0\\m < 0\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m \le \dfrac{1}{3}\\m > 0\end{array} \right.\\\left\{ \begin{array}{l}m \ge \dfrac{1}{3}\\m < 0\end{array} \right.\end{array} \right.\)\( \Leftrightarrow 0 < m \le \dfrac{1}{3}\). Kết hợp 2 trường hợp ta được: \(0 \le m \le \dfrac{1}{3}\) Chọn A. Câu 20 (TH) - Bất phương trình và hệ bất phương trình một ẩn Phương pháp: Thay từng điểm vào hệ bất phương trình. Nếu thỏa mãn thì điểm đó thuộc miền nghiệm của hệ bất phương trình. Cách giải: +) Với \(\left( {x;\,\,y} \right) = \left( { - 1;\,\,4} \right)\) bất phương trình trở thành \(\left\{ \begin{array}{l}2.\left( { - 1} \right) + 3.4 - 1 > 0\\5.\left( { - 1} \right) - 4 + 4 < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}9 > 0\\ - 5 < 0\end{array} \right.\) (thỏa mãn) \( \Rightarrow \) Điểm \(\left( { - 1;\,\,4} \right)\) thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x + 3y - 1 > 0\\5x - y + 4 < 0\end{array} \right.\) +) Với \(\left( {x;\,\,y} \right) = \left( { - 2;\,\,4} \right)\) bất phương trình trở thành \(\left\{ \begin{array}{l}2.\left( { - 2} \right) + 3.4 - 1 > 0\\5.\left( { - 2} \right) - 4 + 4 < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}7 > 0\\ - 10 < 0\end{array} \right.\)(thỏa mãn) \( \Rightarrow \) Điểm \(\left( { - 2;\,\,4} \right)\) thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x + 3y - 1 > 0\\5x - y + 4 < 0\end{array} \right.\) +) Với \(\left( {x;\,\,y} \right) = \left( {1;\,\,0} \right)\) bất phương trình trở thành \(\left\{ \begin{array}{l}2.1 + 3.0 - 1 > 0\\5.1 - 0 + 4 < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}1 > 0\\9 < 0\end{array} \right.\)(vô lý) \( \Rightarrow \) Điểm \(\left( {1;\,\,0} \right)\) không thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x + 3y - 1 > 0\\5x - y + 4 < 0\end{array} \right.\) +) Với \(\left( {x;\,\,y} \right) = \left( { - 3;\,\,4} \right)\) bất phương trình trở thành \(\left\{ \begin{array}{l}2.\left( { - 3} \right) + 3.4 - 1 > 0\\5.\left( { - 3} \right) - 4 + 4 < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}5 > 0\\ - 15 < 0\end{array} \right.\)(thỏa mãn) \( \Rightarrow \) Điểm \(\left( { - 3;\,\,4} \right)\) thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x + 3y - 1 > 0\\5x - y + 4 < 0\end{array} \right.\) Chọn C. Câu 21 (TH) - Bất phương trình Phương pháp: Giải bất phương trình, tìm các giá trị nguyên của \(x\) là nghiệm của bất phương trình và thỏa mãn \(\left[ { - 6;\,\,6} \right]\). Cách giải: \(\begin{array}{l}x\left( {3 - x} \right) \ge x\left( {7 - x} \right) - 6\left( {x - 1} \right)\\ \Leftrightarrow 3x - {x^2} \ge 7x - {x^2} - 6x + 6\\ \Leftrightarrow 3x - 7x + 6x - 6 \ge 0\\ \Leftrightarrow 2x - 6 \ge 0\\ \Leftrightarrow 2x \ge 6\\ \Leftrightarrow x \ge 3\end{array}\) Kết hợp điều kiện đề bài \(x \in \left[ { - 6;\,\,6} \right]\)\( \Rightarrow x \in \left[ {3;6} \right]\). Tổng tất cả các giá trị nguyên của \(x\) thỏa mãn \(\left[ { - 6;\,\,6} \right]\) là: \(3 + 4 + 5 + 6 = 18\) Chọn B. Câu 22 (TH) - Dấu của tam thức bậc hai Phương pháp: Xét hai trường hợp: \(2m = 0\) và \(2m \ne 0\) và sử dụng điều kiện vô nghiệm của phương trình bậc hai \(\Delta < 0\). Cách giải: +) Với \(m = 0\), phương trình trở thành \(3 = 0\) (vô lý) \( \Rightarrow \) Phương trình \(2m{x^2} - 2mx + 3 = 0\) vô nghiệm khi \(m = 0\) \(\left( 1 \right)\) +) Với \(m \ne 0\): Phương trình \(2m{x^2} - 2mx + 3 = 0\) vô nghiệm \( \Leftrightarrow \Delta < 0 \Leftrightarrow 4{m^2} - 24m < 0\\ \Leftrightarrow 4m\left( {m - 6} \right) < 0 \Leftrightarrow 0 < m < 6\) \(\left( 2 \right)\) Kết hợp \(\left( 1 \right)\)và \(\left( 2 \right)\)ta được: \(0 \le m < 6\) Chọn D. Câu 23 (TH) - Bất phương trình Phương pháp: Phá dấu giá trị tuyệt đối và giải bất phương trình. Cách giải: ĐKXĐ: \(x \ne - 1\) TH1: \(x + 1 > 0 \Leftrightarrow x > - 1\) \( \Rightarrow \left| {x + 1} \right| = x + 1\) \(\begin{array}{l}{\mathop{\rm BPT}\nolimits} \Leftrightarrow \dfrac{{{x^2} + 2x - 8}}{{x + 1}} < 0\\ \Leftrightarrow \left\{ \begin{array}{l}{x^2} + 2x - 8 < 0\\x + 1 > 0\end{array} \right.\\\, \Leftrightarrow \left\{ \begin{array}{l} - 4 < x < 2\\x > - 1\end{array} \right.\\ \Leftrightarrow - 1 < x < 2\end{array}\) TH2: \(x + 1 < 0 \Leftrightarrow x < - 1\) \( \Rightarrow \left| {x + 1} \right| = - \left( {x + 1} \right)\) \(\begin{array}{l}{\mathop{\rm BPT}\nolimits} \Leftrightarrow \dfrac{{{x^2} + 2x - 8}}{{ - \left( {x + 1} \right)}} < 0\\\, \Leftrightarrow \left\{ \begin{array}{l}{x^2} + 2x - 8 < 0\\x + 1 < 0\end{array} \right.\\\, \Leftrightarrow \left\{ \begin{array}{l} - 4 < x < 2\\x < - 1\end{array} \right.\\\, \Leftrightarrow - 4 < x < - 1\end{array}\) Kết hợp \(2\) trường hợp trên, tập nghiệm của bất phương trình là \(\left( { - 4;\,\, - 1} \right) \cup \left( { - 1;\,\,2} \right)\). Chọn B. Câu 24 (TH) - Tích vô hướng của hai vectơ Phương pháp: Xác định VTPT của \(AH\) và \(BK\). Áp dụng công thức: \(\cos \left( {{{\vec n}_{AH}},\,\,{{\vec n}_{BK}}} \right) = \dfrac{{\left| {{{\vec n}_{AH}}.{{\vec n}_{BK}}} \right|}}{{\left| {{{\vec n}_{AH}}} \right|.\left| {{{\vec n}_{BK}}} \right|}}\) Cách giải: \(A\left( { - 1;\,\,6} \right),\,\,B\left( {0;\,\,2} \right),\,\,C\left( {1;\,\,5} \right)\)\( \Rightarrow \overrightarrow {BC} = \left( {1;\,\,3} \right),\,\,\overrightarrow {AC} = \left( {2;\,\, - 1} \right)\) Vì \(AH \bot BC\) nên \(\overrightarrow {BC} \) là VTPT của đường thẳng \(AH\) suy ra \({\vec n_{AH}} = \overrightarrow {BC} = \left( {1;\,\,3} \right)\). Vì \(BK \bot AC\) nên \(\overrightarrow {AC} \) là VTPT của đường thẳng \(BK\) suy ra \({\vec n_{BK}} = \overrightarrow {AC} = \left( {2;\,\, - 1} \right)\). \( \Rightarrow \cos \alpha = \cos \left( {{{\vec n}_{AH}},\,\,{{\vec n}_{BK}}} \right)\)\( = \dfrac{{\left| {{{\vec n}_{AH}}.{{\vec n}_{BK}}} \right|}}{{\left| {{{\vec n}_{AH}}} \right|.\left| {{{\vec n}_{BK}}} \right|}}\)\( = \dfrac{{\left| {1.2 + 3.\left( { - 1} \right)} \right|}}{{\sqrt {{1^2} + {3^2}} .\sqrt {{2^2} + {{\left( { - 1} \right)}^2}} }}\)\( = \dfrac{1}{{\sqrt {50} }} = \dfrac{1}{{5\sqrt 2 }}\) Chọn D. Câu 25 (TH) - Bất phương trình Phương pháp: Hai bất phương trình được gọi là tương đương nếu nó có cùng tập nghiệm. Cách giải: *) Xét đáp án A \({x^2}\left( {x + 2} \right) < 0\) \( \Leftrightarrow \left\{ \begin{array}{l}{x^2} > 0\\x + 2 < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x < - 2\end{array} \right.\)\( \Leftrightarrow x < - 2\) \(x + 2 < 0 \Leftrightarrow x < - 2\) \( \Rightarrow \) Cặp bất phương trình \({x^2}\left( {x + 2} \right) < 0\) và \(x + 2 < 0\) tương đương. *) Xét đáp án B \(2{x^2}\left( {x + 1} \right) \le 0\) \( \Leftrightarrow \left\{ \begin{array}{l}2{x^2} \ge 0\\x + 1 \le 0\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\x \le - 1\end{array} \right.\) \(x + 1 \le 0 \Leftrightarrow x \le - 1\) \( \Rightarrow \) Cặp bất phương trình \(2{x^2}\left( {x + 1} \right) \le 0\) và \(x + 1 \le 0\) không tương đương *) Xét đáp án C: ĐKXĐ: \(x \ge 1\) Vì \(x \ge 1 \Leftrightarrow 2x \ge 2\)\( \Leftrightarrow 2x - 1 \ge 1 > 0\). Khi đó, ta có: \(\left( {2x - 1} \right)\sqrt {x - 1} \ge x\left( {2x - 1} \right)\)\( \Leftrightarrow \sqrt {x - 1} \ge x\) \( \Rightarrow \) Cặp bất phương trình \(\sqrt {x - 1} \ge x\) và \(\left( {2x - 1} \right)\sqrt {x - 1} \ge x\left( {2x - 1} \right)\) tương đương *) Xét đáp án D: \(2x + 1 + \dfrac{1}{{x - 2}} < \dfrac{1}{{x - 2}}\)\( \Leftrightarrow \left\{ \begin{array}{l}x - 2 \ne 0\\2x + 1 < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ne 2\\x < - \dfrac{1}{2}\end{array} \right.\)\( \Leftrightarrow x < - \dfrac{1}{2}\) \(2x + 1 < 0 \Leftrightarrow x < - \dfrac{1}{2}\) \( \Rightarrow \) Cặp bất phương trình \(2x + 1 + \dfrac{1}{{x - 2}} < \dfrac{1}{{x - 2}}\)và \(2x + 1 < 0\) tương đương. Chọn B. Câu 26 (TH) - Phương trình đường thẳng Phương pháp: Phương trình đường trung trực của đoạn thẳng \(AB\) đi qua trung điểm của \(AB\) và nhận \(\overrightarrow {AB} \) là VTPT. Cách giải: Gọi \(M\left( {{x_M};\,\,{y_M}} \right)\) là trung điểm của \(AB\) \(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}{x_M} = \dfrac{{{x_A} + {x_B}}}{2}\\{y_M} = \dfrac{{{y_A} + {y_B}}}{2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_M} = \dfrac{{1 + 3}}{2}\\{y_M} = \dfrac{{ - 2 + 6}}{2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_M} = 2\\{y_M} = 2\end{array} \right. \Rightarrow M\left( {2;\,\,2} \right)\end{array}\) \(A\left( {1;\,\, - 2} \right),\,\,B\left( {3;\,\,6} \right) \Rightarrow \overrightarrow {AB} = \left( {2;\,\,8} \right)\) Giả sử \(d\) là đường trung trực của \(AB\). \( \Rightarrow \) \(d\) đi qua \(M\left( {2;\,\,2} \right)\) nhận \(\overrightarrow {AB} = \left( {2;\,\,8} \right)\) là VTPT. \( \Rightarrow \) PTTQ của \(d\) là: \(2.\left( {x - 2} \right) + 8.\left( {y - 2} \right) = 0\)\( \Leftrightarrow x + 4y - 10 = 0\) Chọn C. Câu 27 (TH) - Bất phương trình Phương pháp: Tìm ĐKXĐ và áp dụng nếu \(\left| a \right| > a\) thì \(a < 0\). Cách giải: ĐKXĐ: \(5 - x > 0 \Leftrightarrow x < 5\) \(\dfrac{{\left| {{x^2} - 8x + 12} \right|}}{{\sqrt {5 - x} }} > \dfrac{{{x^2} - 8x + 12}}{{\sqrt {5 - x} }}\) \( \Leftrightarrow \left| {{x^2} - 8x + 12} \right| > {x^2} - 8x + 12\) \(\begin{array}{l} \Leftrightarrow {x^2} - 8x + 12 < 0\\ \Leftrightarrow 2 < x < 6\end{array}\) Kết hợp với ĐKXĐ suy ra bất phương trình đã cho có nghiệm \(x \in \left( {2;\,\,5} \right)\). Mà \(x \in \mathbb{Z} \Rightarrow x \in \left\{ {3;\,\,4} \right\}\). Vậy bất phương trình đã cho không có nghiệm nguyên âm. Chọn D. Câu 28 (TH) - Bất phương trình Phương pháp: Bất phương trình \(\left( {{m^2} - 4} \right){x^2} + \left( {m - 2} \right)x + 1 \le 0\) có nghiệm với mọi \(x \in R\) \( \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta \le 0\end{array} \right.\) Cách giải: Bất phương trình \(\left( {{m^2} - 4} \right){x^2} + \left( {m - 2} \right)x + 1 \le 0\) có nghiệm với mọi \(x \in R\) \( \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta \le 0\end{array} \right.\) +) \(a < 0 \Leftrightarrow {m^2} - 4 < 0 \Leftrightarrow - 2 < m < 2\) +) \(\Delta \le 0\\ \Leftrightarrow {\left( {m - 2} \right)^2} - 4.\left( {{m^2} - 4} \right).1 \le 0 \\\Leftrightarrow - 3{m^2} - 4m + 20 \le 0 \\\Leftrightarrow \left[ \begin{array}{l}m \le \dfrac{{ - 10}}{3}\\m \ge 2\end{array} \right.\) Vậy không có giá trị của \(m\) để bất phương trình có nghiệm với mọi \(x \in R\). Chọn A. Câu 29 (VD) - Phương trình bậc hai Phương pháp: Phương trình bậc hai có hai nghiệm dương phân biệt khi và chỉ khi \(\left\{ \begin{array}{l}a \ne 0\\\Delta > 0\\P > 0\\S > 0\end{array} \right.\) Cách giải: Phương trình \(\left( {m - 1} \right){x^2} - 2\left( {m + 1} \right)x + m + 4 = 0\) có hai nghiệm dương phân biệt khi và chỉ khi \(\left\{ \begin{array}{l}a \ne 0\\\Delta > 0\\{x_1}{x_2} > 0\\{x_1} + {x_2} > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m - 1 \ne 0\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\4{\left( {m + 1} \right)^2} - 4\left( {m - 1} \right)\left( {m + 4} \right) > 0\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\\\dfrac{{m + 4}}{{m - 1}} > 0\,\,\,\,\,\,\,\,\,\,\left( 3 \right)\\\dfrac{{m + 1}}{{m - 1}} > 0\,\,\,\,\,\,\,\,\,\,\left( 4 \right)\end{array} \right.\) Giải \(\left( 1 \right)\): \(m - 1 \ne 0 \Leftrightarrow m \ne 1\) Giải \(\left( 2 \right)\): \(\begin{array}{l}4{\left( {m + 1} \right)^2} - 4\left( {m - 1} \right)\left( {m + 4} \right) > 0\\ \Leftrightarrow \left( {4{m^2} + 8m + 4} \right) \\- \left( {4m - 4} \right)\left( {m + 4} \right) > 0\\ \Leftrightarrow 4{m^2} + 8m + 4 - 4{m^2} - 16m \\+ 4m + 16 > 0\\ \Leftrightarrow - 4m + 20 > 0\\ \Leftrightarrow m < 5\end{array}\) Giải \(\left( 3 \right)\): \(\dfrac{{m + 4}}{{m - 1}} > 0\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m + 4 > 0\\m - 1 > 0\end{array} \right.\\\left\{ \begin{array}{l}m + 4 < 0\\m - 1 < 0\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m > - 4\\m > 1\end{array} \right.\\\left\{ \begin{array}{l}m < - 4\\m < 1\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}m > 1\\m < - 4\end{array} \right.\) Giải \(\left( 4 \right)\): \(\dfrac{{m + 1}}{{m - 1}} > 0\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m + 1 > 0\\m - 1 > 0\end{array} \right.\\\left\{ \begin{array}{l}m + 1 < 0\\m - 1 < 0\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m > - 1\\m > 1\end{array} \right.\\\left\{ \begin{array}{l}m < - 1\\m < 1\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}m > 1\\m < - 1\end{array} \right.\) Kết hợp cả \(4\) điều kiện ta được \(m < - 4\) hoặc \(1 < m < 5\). Chọn A. Câu 30 (TH) - Phương trình đường thẳng Phương pháp: \(\left( {{d_1}} \right),\,\,\left( {{d_2}} \right),\,\,\left( {{d_3}} \right)\) đồng quy nếu \(\left\{ \begin{array}{l}{d_1} \cap \,{d_2} = \left\{ A \right\}\\A \in \left( {\,{d_3}} \right)\end{array} \right.\) (xác định giao điểm của hai đường thẳng sau đó chứng minh giao điểm đó nằm trên đường thẳng thứ ba) Cách giải: \(\left( {{d_1}} \right):\,\,2x - y + 1 = 0\), \(\left( {{d_{^2}}} \right):\,\,x - y + 2 = 0\), \(\left( {{d_{^3}}} \right):\,\,\left( {1 + {m^2}} \right)x - y + 2m - 1 = 0\) Gọi \(\left( {{d_1}} \right) \cap \left( {{d_2}} \right) = A\left( {{x_A};\,\,{y_A}} \right)\). Tọa độ điểm \(A\left( {{x_A};\,\,{y_A}} \right)\) là nghiệm của hệ phương trình: \(\begin{array}{l}\,\left\{ \begin{array}{l}2{x_A} - {y_A} + 1 = 0\\{x_A} - {y_A} + 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2{x_A} - {y_A} = - 1\\{x_A} - {y_A} = - 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 1\\{y_A} = 3\end{array} \right. \Rightarrow A\left( {1;\,\,3} \right)\end{array}\) Để \(\left( {{d_1}} \right),\,\,\left( {{d_2}} \right),\,\,\left( {{d_3}} \right)\) đồng quy thì \(A\left( {1;\,\,3} \right) \in \left( {{d_3}} \right):\left( {1 + {m^2}} \right)x - y \)\(+ 2m - 1 = 0\). \(\begin{array}{l} \Rightarrow \left( {1 + {m^2}} \right).1 - 3 + 2m - 1 = 0\\ \Leftrightarrow 1 + {m^2} - 3 + 2m - 1 = 0\\ \Leftrightarrow {m^2} + 2m - 3 = 0\\ \Leftrightarrow \left( {m - 1} \right)\left( {m + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 1 = 0\\m + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 3\end{array} \right.\end{array}\) Vậy \(m \in \left\{ {1;\,\, - 3} \right\}\). Chọn A. HocTot.XYZ
|