Đề số 34 - Đề thi vào lớp 10 môn ToánĐề thi vào lớp 10 môn Toán - Đề số 34 có đáp án và lời giải chi tiết Đề bài Câu 1 (2 điểm): a) Bằng các phép biến đổi đại số hãy rút gọn biểu thức: \(A = 2\sqrt 5 + 3\sqrt {45} .\) b) Giải phương trình \({x^2} - 6x + 5 = 0.\) Câu 2 (1,5 điểm): Cho hai hàm số \(y = {x^2}\) và \(y = - x + 2.\) a) Vẽ đồ thị của hai hàm số này trên cùng một mặt phẳng tọa độ Oxy. b) Tìm tọa độ giao điểm của hai đồ thị đó bằng phương pháp đại số. Câu 3 (1,5 điểm): Cho phương trình \({x^2} - 2x + m + 3 = 0\;\;\;\left( 1 \right)\) (với \(x\) là ẩn, \(m\) là tham số). a) Tìm tất cả các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có nghiệm. b) Gọi \({x_1},\;{x_2}\) là nghiệm của phương trình \(\left( 1 \right).\) Tìm tất cả các giá trị của \(m\) để \(x_1^2 + x_2^2 - 3{x_1}{x_2} - 4 = 0.\) Câu 4 (1,5 điểm): Một mảnh đất hình chữ nhật có diện tích \(360{m^2}.\) Nếu tăng chiều rộng \(2m\) và giảm chiều dài \(6m\) thì diện tích mảnh đất không đổi. Tính chu vi của mảnh đất lúc đầu. Câu 5 (3,5 điểm): Cho đường tròn \(\left( O \right)\) đường kính \(AB = 6cm.\) Gọi \(H\) là điểm thuộc đoạn thẳng \(AB\) sao cho \(AH = 1cm.\) Qua \(H\) vẽ đường thẳng vuông góc với \(AB,\) đường thẳng này cắt đường tròn \(\left( O \right)\) tại C và D. Hai đường thẳng BC và AD cắt nhau tại M. Gọi N là hình chiếu của M trên đường thẳng AB. a) Chứng minh tứ giác MNAC nội tiếp. b) Tính độ dài CH và \(\tan \angle ABC\) c) Chứng minh NC là tiếp tuyến của đường tròn \(\left( O \right)\). d) Tiếp tuyến tại A của đường tròn \(\left( O \right)\) cắt NC tại E. Chứng minh đường thẳng EB đi qua trung điểm của đoan thẳng CH. Lời giải chi tiết Câu 1: a) Bằng các phép biến đổi đại số hãy rút gọn biểu thức: \(A = 2\sqrt 5 + 3\sqrt {45} .\) \(A = 2\sqrt 5 + 3\sqrt {45} = 2\sqrt 5 + 3.\sqrt {{3^2}.5}\)\(\, = 2\sqrt 5 + 9\sqrt 5 = 11\sqrt 5 .\) Vậy \(A = 11\sqrt 5 .\) b) Giải phương trình \({x^2} - 6x + 5 = 0.\) \(\begin{array}{l}\;\;\;{x^2} - 6x + 5 = 0 \\\Leftrightarrow {x^2} - 5x - x + 5 = 0\\ \Leftrightarrow x\left( {x - 5} \right) - \left( {x - 5} \right) = 0\\ \Leftrightarrow \left( {x - 5} \right)\left( {x - 1} \right) = 0 \\\Leftrightarrow \left[ \begin{array}{l}x - 5 = 0\\x - 1 = 0\end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}x = 5\\x = 1\end{array} \right..\end{array}\) Vậy tập nghiệm của phương trình là: \(S = \left\{ {1;\;5} \right\}.\) Câu 2: Cho hai hàm số \(y = {x^2}\) và \(y = - x + 2.\) a) Vẽ đồ thị của hai hàm số này trên cùng một mặt phẳng tọa độ Oxy. +) Vẽ đồ thị hàm số: \(\left( d \right):\;\;y = - x + 2.\)
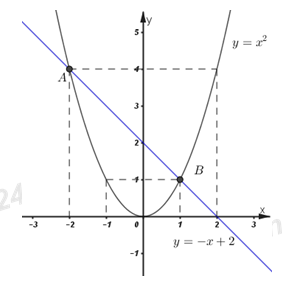
Đồ thị hàm số \(y = - x + 2\) là đường thẳng đi qua các điểm \(\left( {0;\;2} \right),\;\left( {2;\;0} \right).\) +) Vẽ đồ thị hàm số: \(\left( P \right):\;\;y = {x^2}.\)
Đồ thị hàm số \(\left( P \right):\;\;y = {x^2}\) là đường cong đi qua các điểm \(\left( { - 2;\;4} \right),\;\left( { - 1;\;1} \right),\;\left( {0;\;0} \right),\;\left( {1;\;1} \right),\;\left( {2;\;4} \right).\) Đồ thị hàm số:
b) Tìm tọa độ giao điểm của hai đồ thị đó bằng phương pháp đại số. Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình hoành độ giao điểm. Ta có phương trình hoành độ giao điểm của hai đồ thị là: \(\begin{array}{l}\;\;\; - x + 2 = {x^2} \Leftrightarrow {x^2} + x - 2 = 0 \\\Leftrightarrow {x^2} + 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x + 2} \right) - \left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 2 = 0\\x - 1 = 0\end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}x = - 2 \Rightarrow y = 4\\x = 1 \Rightarrow y = 1\end{array} \right..\end{array}\) Vậy hai đồ thị cắt nhau tại hai điểm phân biệt \(A\left( { - 2;\;4} \right)\) và \(B\left( {1;\;1} \right).\) Câu 3: Cho phương trình \({x^2} - 2x + m + 3 = 0\;\;\;\left( 1 \right)\) (với \(x\) là ẩn, \(m\) là tham số). a) Tìm tất cả các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có nghiệm. Phương trình có nghiệm \( \Leftrightarrow \Delta ' \ge 0 \Leftrightarrow 1 - m - 3 \ge 0\) \( \Leftrightarrow m \le - 2.\) Vậy \(m \le - 2\) thì phương trình đã cho có nghiệm. b) Gọi \({x_1},\;{x_2}\) là nghiệm của phương trình \(\left( 1 \right).\) Tìm tất cả các giá trị của \(m\) để \(x_1^2 + x_2^2 - 3{x_1}{x_2} - 4 = 0.\) Với \(m \le - 2\) thì phương trình có hai nghiệm \({x_1},\;{x_2}.\) Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = m + 3\end{array} \right..\) Theo đề bài ta có: \(x_1^2 + x_2^2 - 3{x_1}{x_2} - 4 = 0\) \(\begin{array}{l} \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - 3{x_1}{x_2} - 4 = 0 \\\Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 5{x_1}{x_2} - 4 = 0\\ \Leftrightarrow 4 - 5\left( {m + 3} \right) - 4 = 0\\ \Leftrightarrow 4 - 5m - 15 - 4 = 0 \\ \Leftrightarrow 5m = - 15\\ \Leftrightarrow m = - 3\;\;\;\left( {tm} \right).\end{array}\) Vậy \(m = - 3\) thỏa mãn điều kiện bài toán. Câu 4: Gọi chiều rộng của mảnh đất đã cho là \(x\;\left( m \right),\;\;\left( {0 < x < 360} \right).\) Gọi chiều dài của mảnh đất đã cho là: \(y\;\left( m \right),\;\;\left( {6 < y < 360,\;y > x} \right).\) Khi đó ta có diện tích của mảnh đất là: \(xy = 360\;\;\;\left( 1 \right).\) Tăng chiều rộng thêm \(2m\) thì chiều rộng mới là: \(x + 2\;\;\left( m \right).\) Giảm chiều dài đi \(6m\) thì chiều dài mới là: \(y - 6\;\;\left( m \right).\) Khi đó diện tích mảnh đất không đổi nên ta có phương trình: \(\left( {x + 2} \right)\left( {y - 6} \right) = xy \) \(\Leftrightarrow 2y - 6x - 12 = 0\;\;\;\;\left( 2 \right).\) Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}xy = 360\\2y - 6x - 12 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}xy = 360\\y = 3x + 6\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}x\left( {3x + 6} \right) = 360\\y = 3x + 6\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}3{x^2} + 6x - 360 = 0\\y = 3x + 6\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x = 10\;\;\;\;\left( {tm} \right)\\x = - 12\;\;\left( {ktm} \right)\end{array} \right.\\y = 3.10 + 6\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 10\\y = 36\;\;\left( {tm} \right)\end{array} \right..\) Vậy chu vi của mảnh vườn lúc đầu là: \(\left( {10 + 36} \right).2 = 92m.\) Câu 5: Cho đường tròn \(\left( O \right)\) đường kính \(AB = 6cm.\) Gọi \(H\) là điểm thuộc đoạn thẳng \(AB\) sao cho \(AH = 1cm.\) Qua \(H\) vẽ đường thẳng vuông góc với \(AB,\) đường thẳng này cắt đường tròn \(\left( O \right)\) tại C và D. Hai đường thẳng BC và AD cắt nhau tại M. Gọi N là hình chiếu của M trên đường thẳng AB. a) Chứng minh tứ giác MNAC nội tiếp. Do \(\angle ACB\) là góc nội tiếp chắn nửa đường tròn nên \(\angle ACB = {90^0} \Rightarrow \angle ACM = {90^0}\). Xét tứ giác \(MNAC\) có \(\angle ACM + \angle ANM = {90^0} + {90^0} = {180^0}\) \( \Rightarrow \) Tứ giác \(MNAC\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).’ b) Tính độ dài CH và \(\tan \angle ABC\) Ta có: \(BH = AB - AH = 6 - 1 = 5\,\,\left( {cm} \right)\) Áp dụng hệ thức lượng trong tam giác vuông ABC có: \(A{H^2} = HA.HB = 1.5 = 5 \Rightarrow AH = \sqrt 5 \,\,\left( {cm} \right)\) \( \Rightarrow \tan \angle ABC = \dfrac{{HA}}{{HB}} = \dfrac{{\sqrt 5 }}{5} = \dfrac{1}{{\sqrt 5 }}\) c) Chứng minh NC là tiếp tuyến của đường tròn \(\left( O \right)\). Ta có \(MN \bot AB;\,\,CH \bot AB \Rightarrow MN//CH\) \( \Rightarrow \angle AMN = \angle ADC\) (so le trong) Mà \(\angle AMN = \angle ACN\) (hai góc nội tiếp cùng chắn cung AN) \( \Rightarrow \angle ACN = \angle ADC\). Mà \(\angle ADC\) nội tiếp chắn cung AC, \(\angle ACN\) ở vị trí góc tạo bởi tiếp tuyến và dây cung chắn cung AC. \( \Rightarrow CN\) là tiếp tuyến của đường tròn \(\left( O \right)\) tại C. d) Tiếp tuyến tại A của đường tròn \(\left( O \right)\) cắt NC tại E. Chứng minh đường thẳng EB đi qua trung điểm của đoan thẳng CH. Kéo dài AE cắt BM tại F. Ta có \(EA = EC\,\,\left( 1 \right)\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow \Delta EAC\) cân tại E \( \Rightarrow \angle EAC = \angle ECA\) \( \Rightarrow {90^0} - \angle EAC = {90^0} - \angle ECA \) \(\Leftrightarrow \angle EFC = \angle ECF \) \(\Rightarrow \Delta EFC\) cân tại E \( \Rightarrow EC = EF\) (2) Từ (1) và (2) \( \Rightarrow EA = EC = EF\) Ta có \(AF \bot AB\,\left( {gt} \right);\,\,CH \bot AB\,\,\left( {gt} \right) \Rightarrow AF//CH\) Gọi \(I = BE \cap AF\), áp dụng định lí Ta-let ta có: \(\dfrac{{HI}}{{AE}} = \dfrac{{BI}}{{BE}};\,\,\dfrac{{CI}}{{EF}} = \dfrac{{BI}}{{BE}} \Rightarrow \dfrac{{HI}}{{AE}} = \dfrac{{CI}}{{EF}}\). Mà \(AE = EF\,\,\left( {cmt} \right) \Rightarrow HI = CI \Rightarrow I\) là trung điểm của HC. (đpcm) HocTot.XYZ
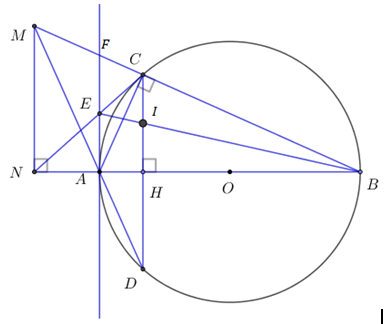
|