Đề thi, đề kiểm tra Toán lớp 6 - Chân trời sáng tạo

Đề thi giữa kì 2 Toán 6 Chân trời sáng tạo - Đề số 7

Tổng hợp đề thi học kì 2 lớp 6 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Khoa học tự nhiên...

Tải về

Làm đề thi

Phần trắc nghiệm (3 điểm) Câu 1 (NB): Trong cách viết sau, cách viết nào cho ta phân số?

Đề bài

I. Trắc nghiệm

Câu 1 :

Trong cách viết sau, cách viết nào cho ta phân số?

A
$\frac{4}{7}$ .
B
$\frac{{0,25}}{{ - 3}}$ .
C
$\frac{5}{0}$ .
D
$\frac{{6,23}}{{7,4}}$ .

Câu 2 :

Số đối của phân số $- \frac{{16}}{{25}}$ là:

A
$\frac{{16}}{{25}}$ .
B
$\frac{{25}}{{16}}$ .
C
$\frac{6}{8}$ .
D
$\frac{{10}}{{75}}$ .

Câu 3 :

Phân số nào sau đây bằng phân số $\frac{3}{4}$ ?

A
$\frac{{13}}{{20}}$ .
B
$\frac{3}{9}$ .
C
$\frac{6}{8}$ .
D
$\frac{{10}}{{75}}$ .

Câu 4 :

Tìm số nguyên $y$ biết $\frac{2}{{ - 3}} = \frac{6}{{ - y}}$ .

A
$2$ .
B
$6$ .
C
$3$ .
D
$9$ .

Câu 5 :

Hình nào dưới đây không có tâm đối xứng

A
Lục giác đều.
B
Tam giác đều.
C
Hình bình hành.
D
Hình thoi.

Câu 6 :

Hình nào dưới đây có trục đối xứng?

A
Hình a), Hình b), Hình c).
B
Hình a), Hình c), Hình d).
C
Hình b), Hình c), Hình d).
D
Hình a) và Hình c).

Câu 7 :

Phát biểu nào dưới đây là đúng?

A
Hình thoi có tâm đối xứng nhưng không có trục đối xứng.
B
Hình thang cân có trục đối xứng, nhưng không có tâm đối xứng.
C
Hình bình hành vừa có tâm đối xứng, vừa có trục đối xứng.
D
Hình chữ nhật có trục đối xứng nhưng không có tâm đối xứng.

Câu 8 :

Trong các chữ cái sau, chữ cái nào nào có tâm đối xứng?

A
Chữ H, I, N.
B
Chữ T, E, C.
C
Chữ E, H, I.
D
Chữ C, H, I.

Câu 9 :

Cho hình vẽ

Số giao điểm tạo bởi 4 đường thẳng trong hình trên là:

A
1 giao điểm.
B
2 giao điểm.
C
3 giao điểm.
D
4 giao điểm.

Câu 10 :

Chọn phát biểu đúng trong các phát biểu sau:

Qua 2 điểm phân biệt ta vẽ được:

A
Chỉ có 1 đường thẳng
B
Không có đường thẳng nào
C
Vô số đường thẳng
D
Có 2 đường thẳng

Câu 11 :

Cho hình vẽ. Hai tia nào đối nhau?

A
Hai tia $OA$ và $OB$ đối nhau.
B
Hai tia $BA$ và $OB$ đối nhau.
C
Hai tia $OA$ và $BO$ đối nhau.
D
Hai tia $AB$ và $OB$ đối nhau.

Câu 12 :

Trong hình vẽ sau đây có bao nhiêu đoạn thẳng?

A
3.
B
4.
C
5.
D
6.

II. Tự luận

Câu 1 :

Thực hiện các phép tính (tính hợp lí nếu có thể):

a) A = $\frac{1}{2}$ + $\frac{1}{3}$

b) $B = \frac{{ - 3}}{7} + \frac{5}{{14}} - \frac{4}{7} + \frac{3}{{12}} + \frac{9}{{14}}$

c) $C = \frac{{25}}{6}:\frac{5}{3} - \left( {\frac{{ - 1}}{4}} \right)$

Câu 2 :

Tìm x, biết:

a) $\frac{{1 - x}}{2} = \frac{8}{{1 - x}}$

b) $\,\frac{1}{5} - \left( {\frac{2}{3} - x} \right) = \frac{{ - 3}}{5}$

Câu 3 :

Một cuốn truyện được An đọc hết trong ba ngày. Biết rằng, ngày thứ nhất An đọc được $\frac{2}{5}$ số trang của cuốn sách. Ngày thứ hai, An đọc được $\frac{7}{{15}}$ số trang của cuốn sách. Ngày thứ ba, An đọc nốt 20 trang còn lại. Hỏi cuốn sách đó có bao nhiêu trang?

Câu 4 :

Cho $Ox$ và $Oy$ là hai tia đối nhau. Trên tia $Ox$ lấy điểm $A$ sao cho $OA = 6cm$ . Trên tia $Oy$ lấy điểm $B$ sao cho $OB = 3cm$ . Gọi $M,N$ lần lượt là trung điểm của $OA,OB$ .

a) Tính $OM,{\rm{ }}ON$ ?

b) Tính độ dài đoạn thẳng $MN$ ?

Câu 5 :

a) Tính tổng $A = \frac{1}{3} + \frac{1}{6} + \frac{1}{{10}} + \frac{1}{{15}} + ... + \frac{1}{{45}}$ .

b) Chứng minh $M = \frac{{n - 1}}{{n - 2}}\,\,\,\left( {n \in {\rm Z}\,;\,n \ne 2} \right)$ là phân số tối giản.

Lời giải và đáp án

I. Trắc nghiệm

Câu 1 :

Trong cách viết sau, cách viết nào cho ta phân số?

A
$\frac{4}{7}$ .
B
$\frac{{0,25}}{{ - 3}}$ .
C
$\frac{5}{0}$ .
D
$\frac{{6,23}}{{7,4}}$ .

Đáp án : A

Phương pháp giải :

Dựa vào khái niệm về phân số.

Lời giải chi tiết :

$\frac{{0,25}}{{ - 3}}$ không phải phân số vì $0,25 \notin \mathbb{Z}$ .

$\frac{5}{0}$ không phải phân số vì 0 nằm ở mẫu.

$\frac{{6,23}}{{7,4}}$ không phải phân số vì $6,23;7,4 \notin \mathbb{Z}$ .

$\frac{4}{7}$ là phân số vì $4;7 \in \mathbb{Z};7 \ne 0$ .

Đáp án A.

Câu 2 :

Số đối của phân số $- \frac{{16}}{{25}}$ là:

A
$\frac{{16}}{{25}}$ .
B
$\frac{{25}}{{16}}$ .
C
$\frac{6}{8}$ .
D
$\frac{{10}}{{75}}$ .

Đáp án : A

Phương pháp giải :

Số đối của phân số $\frac{a}{b}$ là phân số $- \frac{a}{b}$ .

Lời giải chi tiết :

Số đối của phân số $- \frac{{16}}{{25}}$ là $\frac{{16}}{{25}}$ .

Đáp án A.

Câu 3 :

Phân số nào sau đây bằng phân số $\frac{3}{4}$ ?

A
$\frac{{13}}{{20}}$ .
B
$\frac{3}{9}$ .
C
$\frac{6}{8}$ .
D
$\frac{{10}}{{75}}$ .

Đáp án : C

Phương pháp giải :

Sử dụng quy tắc nhân cả tử và mẫu của một phân số: Nếu ta nhân cả tử và mẫu của một phân số với cùng 1 số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.

Lời giải chi tiết :

Ta có: $\frac{3}{4} = \frac{{3.2}}{{4.2}} = \frac{6}{8}$ nên phân số $\frac{6}{8} = \frac{3}{4}$ .

Đáp án C.

Câu 4 :

Tìm số nguyên $y$ biết $\frac{2}{{ - 3}} = \frac{6}{{ - y}}$ .

A
$2$ .
B
$6$ .
C
$3$ .
D
$9$ .

Đáp án : D

Phương pháp giải :

Hai phân số $\frac{a}{b} = \frac{c}{d}$ nếu ad = bc.

Lời giải chi tiết :

Ta có: $\frac{2}{{ - 3}} = \frac{6}{{ - y}}$ nên

$\begin{array}{l}2.\left( { - y} \right) = 6.\left( { - 3} \right)\\ - 2y = - 18\\y=(-18):(-2)\\y = 9\end{array}$

Đáp án D.

Câu 5 :

Hình nào dưới đây không có tâm đối xứng

A
Lục giác đều.
B
Tam giác đều.
C
Hình bình hành.
D
Hình thoi.

Đáp án : B

Phương pháp giải :

Dựa vào kiến thức về tâm đối xứng.

Lời giải chi tiết :

Hình không có tâm đối xứng là tam giác đều.

Đáp án B.

Câu 6 :

Hình nào dưới đây có trục đối xứng?

A
Hình a), Hình b), Hình c).
B
Hình a), Hình c), Hình d).
C
Hình b), Hình c), Hình d).
D
Hình a) và Hình c).

Đáp án : B

Phương pháp giải :

Dựa vào kiến thức về trục đối xứng.

Lời giải chi tiết :

Hình a; c; d có trục đối xứng.

Hình b không có trục đối xứng.

Đáp án B.

Câu 7 :

Phát biểu nào dưới đây là đúng?

A
Hình thoi có tâm đối xứng nhưng không có trục đối xứng.
B
Hình thang cân có trục đối xứng, nhưng không có tâm đối xứng.
C
Hình bình hành vừa có tâm đối xứng, vừa có trục đối xứng.
D
Hình chữ nhật có trục đối xứng nhưng không có tâm đối xứng.

Đáp án : B

Phương pháp giải :

Dựa vào kiến thức về trục đối xứng, tâm đối xứng.

Lời giải chi tiết :

Hình thoi vừa có tâm đối xứng, vừa có trục đối xứng nên A sai.

Hình thang cân có trục đối xứng, nhưng không có tâm đối xứng nên B đúng.

Hình bình hành có tâm đối xứng nhưng không có trục đối xứng nên C sai.

Hình chữ nhật vừa có tâm đối xứng, vừa có trục đối xứng nên D sai.

Đáp án B.

Câu 8 :

Trong các chữ cái sau, chữ cái nào nào có tâm đối xứng?

A
Chữ H, I, N.
B
Chữ T, E, C.
C
Chữ E, H, I.
D
Chữ C, H, I.

Đáp án : A

Phương pháp giải :

Dựa vào kiến thức về tâm đối xứng.

Lời giải chi tiết :

Các chữ cái có tâm đối xứng là H, I, N.

Đáp án A.

Câu 9 :

Cho hình vẽ

Số giao điểm tạo bởi 4 đường thẳng trong hình trên là:

A
1 giao điểm.
B
2 giao điểm.
C
3 giao điểm.
D
4 giao điểm.

Đáp án : D

Phương pháp giải :

Quan sát hình vẽ để trả lời.

Lời giải chi tiết :

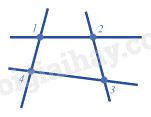
Có 4 giao điểm tạo bởi 4 đường thẳng trong hình trên.

Đáp án D.

Câu 10 :

Chọn phát biểu đúng trong các phát biểu sau:

Qua 2 điểm phân biệt ta vẽ được:

A
Chỉ có 1 đường thẳng
B
Không có đường thẳng nào
C
Vô số đường thẳng
D
Có 2 đường thẳng

Đáp án : A

Phương pháp giải :

Dựa vào kiến thức về điểm và đường thẳng.

Lời giải chi tiết :

Qua hai điểm phân biệt ta chỉ vẽ được 1 đường thẳng nên A đúng.

Đáp án A.

Câu 11 :

Cho hình vẽ. Hai tia nào đối nhau?

A
Hai tia $OA$ và $OB$ đối nhau.
B
Hai tia $BA$ và $OB$ đối nhau.
C
Hai tia $OA$ và $BO$ đối nhau.
D
Hai tia $AB$ và $OB$ đối nhau.

Đáp án : A

Phương pháp giải :

Dựa vào kiến thức về tia.

Lời giải chi tiết :

Hai tia OA và OB là hai tia đối nhau.

Đáp án A.

Câu 12 :

Trong hình vẽ sau đây có bao nhiêu đoạn thẳng?

A
3.
B
4.
C
5.
D
6.

Đáp án : D

Phương pháp giải :

Dựa vào kiến thức về đoạn thẳng.

Lời giải chi tiết :

Có 6 đoạn thẳng trong hình vẽ, đó là: KJ, KL, KN, JL, JN, LN.

Đáp án D.

II. Tự luận

Câu 1 :

Thực hiện các phép tính (tính hợp lí nếu có thể):

a) A = $\frac{1}{2}$ + $\frac{1}{3}$

b) $B = \frac{{ - 3}}{7} + \frac{5}{{14}} - \frac{4}{7} + \frac{3}{{12}} + \frac{9}{{14}}$

c) $C = \frac{{25}}{6}:\frac{5}{3} - \left( {\frac{{ - 1}}{4}} \right)$

Phương pháp giải :

Dựa vào các quy tắc tính với phân số.

Lời giải chi tiết :

a) A = $\frac{1}{2}$ + $\frac{1}{3}$ = $\frac{3}{6} + \frac{2}{6} = \frac{5}{6}$

b) B = $\frac{{ - 3}}{7} + \frac{5}{{14}} - \frac{4}{7} + \frac{3}{{12}} + \frac{9}{{14}}$ $= \left( {\frac{{ - 3}}{7} - \frac{4}{7}} \right) + \left( {\frac{5}{{14}} + \frac{9}{{14}}} \right) + \frac{3}{{12}}$ $= - 1 + 1 + \frac{3}{{12}}$ $= \frac{3}{{12}}$ = $\frac{1}{4}$

c) $C = \frac{{25}}{6}:\frac{5}{3} - \left( {\frac{{ - 1}}{4}} \right)$ $= \frac{{25}}{6}.\frac{3}{5} + \frac{1}{4}$ $= \frac{5}{2} + \frac{1}{4}$ $= \frac{{10}}{4} + \frac{1}{4} = \frac{{11}}{4}$

Câu 2 :

Tìm x, biết:

a) $\frac{{1 - x}}{2} = \frac{8}{{1 - x}}$

b) $\,\frac{1}{5} - \left( {\frac{2}{3} - x} \right) = \frac{{ - 3}}{5}$

Phương pháp giải :

Dựa vào quy tắc tính với phân số để tìm x.

Lời giải chi tiết :

a) $\frac{{1 - x}}{2} = \frac{8}{{1 - x}}$

$\begin{array}{l}{\left( {1 - x} \right)^2} = 8.2\\{\left( {1 - x} \right)^2} = 16\\1 - x = \pm 4\end{array}$

Với $1 - x = 4$

$\begin{array}{l}x = 1 - 4\\x = - 3\end{array}$

Với $1 - x = - 4$

$\begin{array}{l}x = 1 + 4\\x = 5\end{array}$

Vậy $x = - 3$ ; $x = 5$

b) $\frac{1}{5} - \left( {\frac{2}{3} - x} \right) = \frac{{ - 3}}{5}$

$\frac{2}{3} - x = \frac{1}{5} - \frac{{ - 3}}{5}$

$x = \frac{2}{3} - \frac{4}{5}$

Vậy x = $\frac{{ - 2}}{{15}}$

Câu 3 :

Phương pháp giải :

Biểu diễn phân số tương ứng với 20 trang sách. Từ đó tính được số trang sách.

Lời giải chi tiết :

Ngày thứ ba An đọc được 20 trang sách tương ứng với phân số:

$1 - \frac{2}{5} - \frac{7}{{15}} = \frac{2}{{15}}$

Vậy cuốn sách có số trang là: $20:\frac{2}{{15}} = 150$ (trang)

Câu 4 :

a) Tính $OM,{\rm{ }}ON$ ?

b) Tính độ dài đoạn thẳng $MN$ ?

Phương pháp giải :

Vẽ hình theo yêu cầu đề bài.

a) Sử dụng tính chất của trung điểm để tìm OM, ON.

b) Vì O nằm giữa MN nên MN = OM + ON.

Lời giải chi tiết :

a) Do $M$ là trung điểm của $OA$ nên ta có:

$OM = MA = \frac{{OA}}{2} = \frac{6}{2} = 3(cm)$

Do $N$ là trung điểm của $OB$ nên ta có:

$ON = NB = \frac{{OB}}{2} = \frac{3}{2} = 1,5(cm)$

b) Vì điểm $O$ nằm giữa hai điểm $M,N$ nên ta có: $MN = OM + ON$

Suy ra $MN = 3 + 1,5 = 4,5(cm)$

Vậy ${\rm{MN = 4,5 cm}}$ .

Câu 5 :

a) Tính tổng $A = \frac{1}{3} + \frac{1}{6} + \frac{1}{{10}} + \frac{1}{{15}} + ... + \frac{1}{{45}}$ .

b) Chứng minh $M = \frac{{n - 1}}{{n - 2}}\,\,\,\left( {n \in {\rm Z}\,;\,n \ne 2} \right)$ là phân số tối giản.

Phương pháp giải :

a) Nhân cả tử và mẫu của các phân số trong A với 2.

Rút 2 ra ngoài, biến đổi các phân số $\frac{1}{{a\left( {a + 1} \right)}}$ thành $\frac{1}{a} - \frac{1}{{a + 1}}$ (vì $\frac{1}{{a\left( {a + 1} \right)}} = \frac{1}{a} - \frac{1}{{a + 1}}$ )

Tính A.

b) Để chứng minh phân số tổi giản, ta chứng minh ƯCLN của tử số và mẫu số là 1.

Lời giải chi tiết :

a) Ta có $A = \frac{1}{3} + \frac{1}{6} + \frac{1}{{10}} + \frac{1}{{15}} + ... + \frac{1}{{45}} = \frac{2}{6} + \frac{2}{{12}} + \frac{2}{{20}} + \frac{2}{{30}} + ... + \frac{2}{{90}}$

$\begin{array}{l} = 2\left( {\frac{1}{{2.3}} + \frac{1}{{3.4}} + \frac{1}{{4.5}} + \frac{1}{{5.6}} + ... + \frac{1}{{9.10}}} \right)\\ = 2\left( {\frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \frac{1}{4} - \frac{1}{5} + \frac{1}{5} - \frac{1}{6} + ... + \frac{1}{9} - \frac{1}{{10}}} \right)\end{array}$

$= 2\left( {\frac{1}{2} - \frac{1}{{10}}} \right) = 2.\frac{4}{{10}} = \frac{4}{5}$ .

Vậy $A = \frac{4}{5}.$

b) Gọi ƯCLN $\left( {n - 1\,;\,n - 2} \right) = d$ suy ra $n - 1 \vdots d\,\,\,,\,\,n - 2 \vdots d$

suy ra $\left( {n - 1} \right) - \left( {n - 2} \right) \vdots d$ suy ra $1 \vdots d \Rightarrow d = 1$ với mọi $n$

Vậy với mọi $n \in {\rm Z}$ thì $M = \frac{{n - 1}}{{n - 2}}$ là phân số tối giản.

Bài liên quan

Đề thi giữa kì 2 Toán 6 Chân trời sáng tạo - Đề số 8

Phần trắc nghiệm (3 điểm) Câu 1 (NB): Trong các cách viết sau, cách viết nào không phải là phân số?
Đề thi giữa kì 2 Toán 6 Chân trời sáng tạo - Đề số 9

Phần trắc nghiệm (3 điểm) Câu 1 (NB): Phân số nghịch đảo của phân số $\frac{1}{3}$ là
Đề thi giữa kì 2 Toán 6 Chân trời sáng tạo - Đề số 10

Phần trắc nghiệm (3 điểm) Câu 1 (NB): Phân số nào dưới đây không biểu diễn phần tô màu cam trong hình bên:
Đề thi giữa kì 2 Toán 6 Chân trời sáng tạo - Đề số 6

Phần trắc nghiệm (3 điểm) Câu 1 (NB): Trong cách viết sau, cách viết nào cho ta phân số?
Đề thi giữa kì 2 Toán 6 - Đề số 5 - Chân trời sáng tạo

Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.