Đề thi học kì 1 Toán 6 Chân trời sáng tạo - Đề số 18Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:Đề bài
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Cho \(\mathbb{N}\) là tập hợp các số tự nhiên. Cách viết đúng là:
Câu 2 :
Kết quả của phép tính \({2^3} + {5^2}\) là
Câu 3 :
Ước chung lớn nhất của 16 và 20 là:
Câu 4 :
Số đối của -5 là:
Câu 5 :
Tổng các số nguyên thỏa mãn \( - 3 < x < 5\) là
Câu 6 :
Sắp xếp các số nguyên: 2; -5; 7; -3; 0 theo thứ tự tăng dần là:
Câu 7 :
Nhiệt độ buổi trưa ở Sa Pa là \(5^\circ C\). Khi về đêm, nhiệt độ giảm xuống \(9^\circ C\) so với buổi trưa. Hỏi nhiệt độ về đêm ở Sa Pa là bao nhiêu độ C?
Câu 8 :
Tập hợp các ước của 15 là:
Câu 10 :
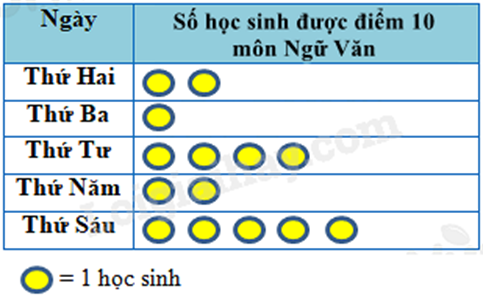
Cho biểu đồ tranh về số học sinh khối lớp 6 được điểm 10 môn Ngữ Văn trong tuần như sau:
Số học sinh được điểm 10 môn Ngữ Văn vào thứ Năm là
Câu 11 :
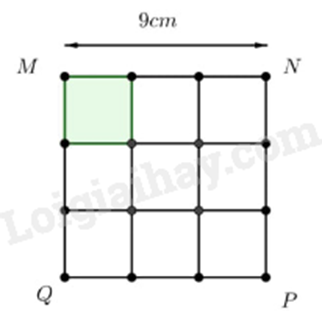
Xếp 9 mảnh hình vuông nhỏ bằng nhau tạo thành hình vuông lớn MNPQ. Biết MN = 9cm. Diện tích một hình vuông nhỏ là:
Câu 12 :
Bạn An làm bông hoa bằng giấy được ghép bởi các hình thoi (như hình dưới đây). Biết diện tích mỗi hình thoi là \(20c{m^2}\). Hỏi diện tích số giấy cần sử dụng để làm bông hoa là bao nhiêu?
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Cho \(\mathbb{N}\) là tập hợp các số tự nhiên. Cách viết đúng là:
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về tập hợp số tự nhiên. Lời giải chi tiết :
Tập hợp \(\mathbb{N}\) được viết là: \(\mathbb{N} = \left\{ {0;1;2;3;4;...} \right\}\) Đáp án B
Câu 2 :
Kết quả của phép tính \({2^3} + {5^2}\) là
Đáp án : A Phương pháp giải :
Thực hiện tính lũy thừa: \({a^n} = a.a.a.....a\) (n thừa số a). Lời giải chi tiết :
\({2^3} + {5^2} = 8 + 25 = 33\). Đáp án A
Câu 3 :
Ước chung lớn nhất của 16 và 20 là:
Đáp án : B Phương pháp giải :
Muốn tìm ƯCLN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau: Bước 1: Phân tích mỗi số ra thừa số nguyên tố. Bước 2: Chọn ra các thừa số nguyên tố chung. Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm. Lời giải chi tiết :
Ta có: \(16 = {2^4}\); \(20 = {2^2}.5\). Suy ra ƯCLN(16,20) = \({2^2} = 4\) Đáp án B
Câu 4 :
Số đối của -5 là:
Đáp án : C Phương pháp giải :
Số đối của a là –a. Lời giải chi tiết :
Số đối của -5 là –(-5) = 5. Đáp án C
Câu 5 :
Tổng các số nguyên thỏa mãn \( - 3 < x < 5\) là
Đáp án : D Phương pháp giải :
Liệt kê các số nguyên thỏa mãn. Tính tổng các số đó. Lời giải chi tiết :
Các số nguyên thỏa mãn \( - 3 < x < 5\) là -2; -1; 0; 1; 2; 3; 4. Tổng của chúng là: -2 + -1 + 0 + 1 + 2 + 3 + 4 = (-2 + 2) + (-1 + 1) + 0 + 3 + 4 = 7. Đáp án D
Câu 6 :
Sắp xếp các số nguyên: 2; -5; 7; -3; 0 theo thứ tự tăng dần là:
Đáp án : C Phương pháp giải :
Chia làm 2 nhóm: số nguyên âm và nguyên dương để xếp thứ tự. Lời giải chi tiết :
Các số nguyên âm là: -5; -3. Vì 5 > 3 nên – 5 < - 3. Các số nguyên dương là: 2; 7. Ta có: 2 < 7. Vậy các số nguyên sắp xếp theo thứ tự tăng dần là: -5; -3; 0; 2; 7. Đáp án C
Câu 7 :
Nhiệt độ buổi trưa ở Sa Pa là \(5^\circ C\). Khi về đêm, nhiệt độ giảm xuống \(9^\circ C\) so với buổi trưa. Hỏi nhiệt độ về đêm ở Sa Pa là bao nhiêu độ C?
Đáp án : B Phương pháp giải :
Sử dụng quy tắc trừ hai số nguyên. Nhiệt độ giảm xuống ta dùng phép trừ. Lời giải chi tiết :
Nhiệt độ về đêm ở Sa Pa là: 5 – 9 = -(9 – 5) = \( - 4\left( {^\circ C} \right)\). Đáp án B
Câu 8 :
Tập hợp các ước của 15 là:
Đáp án : B Phương pháp giải :
Tìm ước nguyên dương của chúng. Số đối của các ước vừa tìm được cũng là một ước. Lời giải chi tiết :
Tập hợp các ước của 15 là: \(\left\{ { \pm 1; \pm 3; \pm 5; \pm 15} \right\}\) Đáp án B
Đáp án : D Phương pháp giải :
Kiểm tra xem Họ và tên hay Năm sinh nào là không hợp lí. Lời giải chi tiết :
Dữ liệu không hợp lí là [email protected] Vì là hỏi năm sinh mà trả lời lại ở dưới dạng gmail. Đáp án D
Câu 10 :
Cho biểu đồ tranh về số học sinh khối lớp 6 được điểm 10 môn Ngữ Văn trong tuần như sau:
Số học sinh được điểm 10 môn Ngữ Văn vào thứ Năm là
Đáp án : B Phương pháp giải :
- Mỗi một hình tròn tương ứng với 1 học sinh được điểm 10 môn Ngữ Văn. - Quan sát hàng “Thứ Năm” để tìm số học sinh được điểm 10. Lời giải chi tiết :
Thứ Năm có 2 hình tròn tương ứng với 2 học sinh được điểm 10 môn Ngữ Văn. Đáp án B
Câu 11 :
Xếp 9 mảnh hình vuông nhỏ bằng nhau tạo thành hình vuông lớn MNPQ. Biết MN = 9cm. Diện tích một hình vuông nhỏ là:
Đáp án : A Phương pháp giải :
Tính diện tích hình vuông lớn. Diện tích hình vuông nhỏ = diện tích hình vuông lớn : 9. Lời giải chi tiết :
Diện tích hình vuông lớn là: 9.9 = \(81\left( {c{m^2}} \right)\) Diện tích hình vuông nhỏ là: 81 : 9 = \(9\left( {c{m^2}} \right)\) Đáp án A
Câu 12 :
Bạn An làm bông hoa bằng giấy được ghép bởi các hình thoi (như hình dưới đây). Biết diện tích mỗi hình thoi là \(20c{m^2}\). Hỏi diện tích số giấy cần sử dụng để làm bông hoa là bao nhiêu?
Đáp án : C Phương pháp giải :
Xác định số hình thoi. Diện tích số giấy cần sử dụng = diện tích hình thoi . số hình thoi. Lời giải chi tiết :
Quan sát hình vẽ, ta thấy bông hoa giấy được tạo thành bởi 8 hình thoi bằng nhau. Vậy diện tích giấy cần sử dụng là: 20 . 8 = \(160\left( {c{m^2}} \right)\) Đáp án C
II. Tự luận
Phương pháp giải :
a) Sử dụng tính chất kết hợp của phép cộng. b) Sử dụng tính chất phân phối của phép nhân đối với phép cộng. c) Thực hiện lần lượt phép nhân, chia, cộng với số nguyên. d) Sử dụng các quy tắc tính với số nguyên và thứ tự thực hiện phép tính: Nếu biểu thức có các dấu ngoặc: ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính theo thứ tự: ( ) → [ ] → { } Lời giải chi tiết :
a) \(\left( { - 2023} \right) + 108 + 2023 - 98\) \(\begin{array}{l} = \left[ {\left( { - 2023} \right) + 2023} \right] + \left( {108 - 98} \right)\\ = 0 + 10\\ = 10\end{array}\) b) \(27.31 + 27.24 + 27.\left( { - 65} \right)\) \(\begin{array}{l} = 27.\left( {31 + 24 - 65} \right)\\ = 27.\left( { - 10} \right)\\ = - 270\end{array}\) c) \(\left( { - 25} \right).\left( { - 3} \right) + 126:\left( { - 9} \right)\) \(\begin{array}{l} = 75 + \left( { - 16} \right)\\ = 59\end{array}\) d) \({2^3}{.2024^0} + \left[ {\left( { - 54} \right) - \left( { - 12 + 48} \right)} \right]\) \(\begin{array}{l} = 8.1 + \left( { - 54 + 12 - 48} \right)\\ = 8 - 54 + 12 - 48\\ = - 46 + 12 - 48\\ = - 34 - 48\\ = - 82\end{array}\) Phương pháp giải :
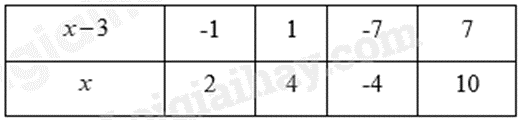
Áp dụng tính chất của đẳng thức, quy tắc dấu ngoặc và quy tắc chuyển vế rồi thực hiện phép tính với các số đã biết. d) \(7 \vdots \left( {x - 3} \right)\) thì \(\left( {x - 3} \right) \in \) Ư(7) Lời giải chi tiết :
a) \(x - 42 = \left( { - 18} \right) + \left( { - 16} \right)\) \(\begin{array}{l}x - 42 = - 34\\x = - 34 + 42\\x = 8\end{array}\) Vậy \(x = 8\) b) \(\left( {5x - 3} \right) + 85 = 32\) \(\begin{array}{l}5x - 3 = 32 - 85\\5x - 3 = - 53\\5x = - 53 + 3\\5x = - 50\\x = - 50:5\\x = - 10\end{array}\) Vậy \(x = - 10\) c) \(2{\left( {x + 1} \right)^2} + 4 = {2^2}{.3^2}\) \(\begin{array}{l}2{\left( {x + 1} \right)^2} + 4 = 4.9\\2{\left( {x + 1} \right)^2} + 4 = 36\\2{\left( {x + 1} \right)^2} = 36 - 4\\2{\left( {x + 1} \right)^2} = 32\\{\left( {x + 1} \right)^2} = 32:2\\{\left( {x + 1} \right)^2} = 16\\x + 1 = \pm 4\end{array}\) TH1: \(x + 1 = 4\) suy ra \(x = 4 - 1 = 3\) TH2: \(x + 1 = - 4\) suy ra \(x = - 4 - 1 = - 5\) Vậy \(x \in \left\{ { - 5;3} \right\}\). d) \(7 \vdots \left( {x - 3} \right)\) Suy ra \(\left( {x - 3} \right) \in \) Ư(7) \( = \left\{ { \pm 1; \pm 7} \right\}\) Ta có bảng giá trị:
Vậy \(x \in \left\{ {2;4; - 4;10} \right\}\). Phương pháp giải :
a) Tính tổng số bạn trong bảng dữ liệu. b) Lập bảng thống kê gồm: Xếp loại học lực và số học sinh. Lời giải chi tiết :
a) Tổ một lớp 6A có 15 học sinh. b) Bảng thống kê: Xếp loại học tập của học sinh tổ một lớp 6A là nhiều nhất loại Khá. Phương pháp giải :
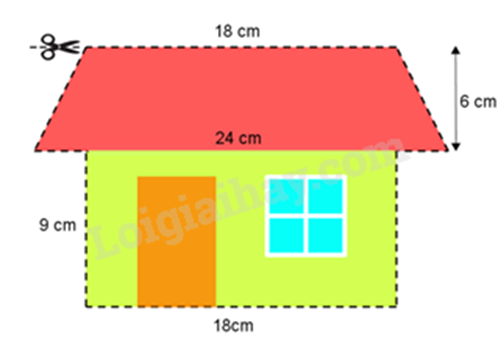
Tính diện tích phần hình thang cân = tổng hai đáy. chiều cao : 2. Tính diện tích phần hình chữ nhật = chiều dài . chiều rộng. Diện tích phần giấy = diện tích hình thang cân + diện tích hình chữ nhật. Lời giải chi tiết :
Diện tích phần hình thang cân là: \(\left( {18 + 24} \right).6:2 = 126\left( {c{m^2}} \right)\) Diện tích phần hình chữ nhật là: \(18.9 = 162\left( {c{m^2}} \right)\) Diện tích phần giấy bạn Minh sẽ cắt là: \(126 + 162 = 288\left( {c{m^2}} \right)\) Vậy diện tích phần giấy bạn Minh sẽ cắt là \(288c{m^2}\). Phương pháp giải :
Cộng cả hai vế với 2. Sử dụng tính chất của phép cộng số nguyên để nhóm x và y. Lời giải chi tiết :
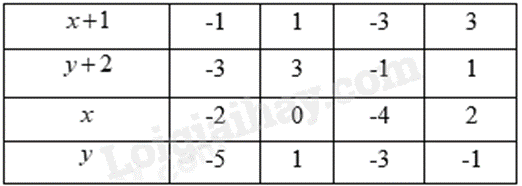
Ta có: \(xy + 2x + y = 1\) Cộng cả hai vế với 2, ta được: \(\begin{array}{l}xy + 2x + y + 2 = 1 + 2\\x\left( {y + 2} \right) + \left( {y + 2} \right) = 3\\\left( {x + 1} \right)\left( {y + 2} \right) = 3\end{array}\) Suy ra \(x + 1\) và \(y + 2\) là các cặp ước tương ứng của 3. Ư(3) = \(\left\{ { \pm 1; \pm 3} \right\}\). Ta có bảng giá trị sau:
Vậy các cặp \(\left( {x;y} \right)\) thỏa mãn là: \(\left( { - 2; - 5} \right);\left( {0;1} \right);\left( { - 4; - 3} \right);\left( {2; - 1} \right)\)
|