Đề thi vào 10 môn Toán Đồng Nai năm 2021

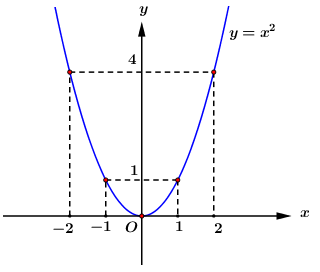
Đề bài

Câu 1 (2,0 điểm):

1) Giải phương trình ${x^2} + 3x - 10 = 0$

2) Giải phương trình $3{x^4} + 2{x^2} - 5 = 0$

3) Giải hệ phương trình $\left\{ \begin{array}{l}2x - 3y = 1\\x + 2y = 4\end{array} \right.$

Câu 2 (2,25 điểm):

1)  Vẽ đồ thị hàm số $\left( P \right):y = {x^2}$.

2) Tìm giá trị của tham số  thực $m$ để Parabol $\left( P \right):y = {x^2}$ và đường thẳng  $\left( d \right):y = 2x - 3m$ có đúng một điểm chung.

3) Cho phương trình ${x^2} + 5x - 4$. Gọi ${x_1},{x_2}$ là hai nghiệm phân biệt của phương trình, hãy tính giá trị của biểu thức $Q = {x_1}^2 + {x_2}^2 + 6{x_1}{x_2}$

Câu 3 (1,0 điểm):

Rút gọn biểu thức $A = \left( {\dfrac{{x - 4}}{{\sqrt x  - 2}} + \dfrac{{x - 2\sqrt x }}{{\sqrt x }}} \right):\sqrt x$ (với $x > 0,\,\,x \ne 4$).

Câu 4 (1,75 điểm):

1) Hằng ngày bạn Mai đi học bằng xe đạp, quãng đường từ nhà đến trường dài 3 km. Hôm nay, xe đạp hư nên Mai nhờ mẹ chở đi đến trường bằng xe máy với vận tốc lớn hơn vận tốc khi đi xe đạp là 24 km/h, cùng một thời điểm khởi hành như mọi ngày nhưng Mai đã đến trường sớm hơn 10 phút. Tính vận tốc của bạn Mai khi đi học bằng xe đạp.

2) Cho $\Delta ABC$ vuông tại $A$, biết $AB = a,\,\,AC = 2a$ (với $a$ là số thực dương). Tính thể tích theo $a$ của hình nón được tạo thành khi quay $\Delta ABC$ một vòng quanh cạnh $AC$ cố định.

Câu 5 (3,0 điểm):

Cho tam giác $ABC$ có ba góc nhọn $\left( {AB < AC} \right)$. Ba đường cao $AD,\,\,BE,\,\,CF$ cắt nhau tại $H$.

1)  Chứng minh tứ giác $BFEC$ nội tiếp. Xác định tâm $O$ của đườn trọn ngoại tiếp tứ giác $BFEC$.

2) Gọi $I$ là trung điểm của AH. Chứng minh $IE$ là tiếp tuyến của đường tròn $\left( O \right)$.

3) Vẽ $CI$ cắt đường tròn $\left( O \right)$ tại $M\left( {M \ne C} \right)$, $FE$ cắt $AD$ tại $K$. Chứng minh $B,K,M$ thẳng hàng.

Lời giải chi tiết

Câu 1

Phương pháp:

1) Sử dụng công thức nghiệm của phương trình bậc hai một ẩn.

2) Đặt $t = {x^2}\,\,\left( {t \ge 0} \right)$, đưa phương trình ban đầu về phương trình bậc hai một ẩn

Nhẩm nhanh hệ số và tính được nghiệm của phương trình

3) Sử dụng phương pháp cộng đại số, tìm được nghiệm của hệ phương trình.

Cách giải:

1) Ta có: $\Delta  = {3^2} - 4.\left( { - 10} \right) = 49 > 0$ nên phương trình có 2 nghiệm phân biệt $\left[ \begin{array}{l}{x_1} = \dfrac{{ - 3 + \sqrt {49} }}{2} = 2\\{x_2} = \dfrac{{ - 3 - \sqrt {49} }}{2} =  - 5\end{array} \right.$.

Vậy tập nghiệm của phương trình là $S = \left\{ {2; - 5} \right\}$.

2) Đặt $t = {x^2}\,\,\left( {t \ge 0} \right)$, phương trình đã cho trở thành $3{t^2} + 2t - 5 = 0$.

Ta có $a + b + c = 2 + 3 - 5 = 0$ nên phương trình có 2 nghiệm phân biệt $\left[ \begin{array}{l}{t_1} = 1\,\,\left( {tm} \right)\\{t_2} = \dfrac{c}{a} =  - \dfrac{5}{3}\,\,\left( {ktm} \right)\end{array} \right.$.

Với $t = 1 \Rightarrow {x^2} = 1 \Leftrightarrow x =  \pm 1$.

Vậy tập nghiệm của phương trình $S = \left\{ { - 1;1} \right\}$.

3) Ta có: $\left\{ \begin{array}{l}2x - 3y = 1\\x + 2y = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - 3y = 1\\2x + 4y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7y = 7\\x = 4 - 2y\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 2\end{array} \right.$

Vậy hệ phương trình có nghiệm $\left( {x;y} \right) = \left( {2;1} \right)$.

Bài 2

Phương pháp:

1) Lập bảng giá trị tương ứng của $x$ và $y$, tìm được các điểm của đồ thị $\left( P \right)$ đi qua, từ đó vẽ được $\left( P \right)$

2) + Xét phương trình hoành độ giao điểm của $\left( P \right),\left( d \right)$ là phương trình bậc hai một ẩn (1)

+ Để $\left( P \right)$ cắt $\left( d \right)$ có đúng một điểm chung khi và chỉ khi $\left( 1 \right)$ có nghiệm kép $\Delta ' = 0$

3) Áp dụng hệ thức Vi – ét, tính được ${x_1} + {x_2};{x_1}.{x_2}$ thay vào biểu thức $Q$ và tính.

Cách giải:

1) Parabol $\left( P \right):\,\,y = {x^2}$ có bề lõm hướng lên và nhận $Oy$ làm trục đối xứng.

Ta có bảng giá trị sau:

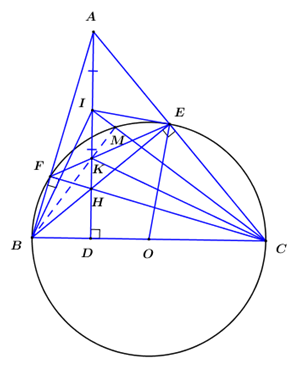
$\Rightarrow$ Parabol $\left( P \right):\,\,y = {x^2}$ đi qua các điểm $\left( { - 2;4} \right)$, $\left( { - 1;1} \right)$, $\left( {0;0} \right)$, $\left( {1;1} \right)$, $\left( {2;4} \right)$.

Đồ thị Parabol $\left( P \right):\,\,y = {x^2}$:

2) Xét phương trình hoành độ giao điểm của $\left( P \right),\left( d \right)$ ta được:

${x^2} = 2x - 3m \Leftrightarrow {x^2} - 2x + 3m = 0\,\,\,\,\left( 1 \right)$

Để $\left( P \right)$ cắt $\left( d \right)$ có đúng một điểm chung khi và chỉ khi $\left( 1 \right)$ có nghiệm kép

$\Leftrightarrow \Delta ' = 0 \Leftrightarrow 1 - 3m = 0 \Leftrightarrow m = \dfrac{1}{3}$

Vậy $m = \dfrac{1}{3}$ thỏa mãn yêu cầu bài toán.

3) Vì ${x_1},{x_2}$ là hai nghiệm phân biệt của phương trình đã cho nên áp dụng hệ thức Vi-et với phương trình ${x^2} + 5x - 4 = 0$ ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} =  - 5\\{x_1}{x_2} =  - 4\end{array} \right.$.

Ta có: $Q = {x_1}^2 + {x_2}^2 + 6{x_1}{x_2} = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} + 6{x_1}{x_2} = {\left( {{x_1} + {x_2}} \right)^2} + 4{x_1}{x_2}$

$\Rightarrow Q = {\left( { - 5} \right)^2} + 4\left( { - 4} \right) = 9$

Vậy $Q = 9$.

Câu 3 (1,0 điểm):

Phương pháp:

Xác định mẫu thức chung, quy đồng, thực hiện các phép toán với để rút gọn biểu thức $A$

Cách giải:

Với $x > 0,\,\,x \ne 4$ ta có:

$\begin{array}{l}A = \left( {\dfrac{{x - 4}}{{\sqrt x  - 2}} + \dfrac{{x - 2\sqrt x }}{{\sqrt x }}} \right):\sqrt x \\A = \left( {\dfrac{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}{{\sqrt x  - 2}} + \dfrac{{\sqrt x \left( {\sqrt x  - 2} \right)}}{{\sqrt x }}} \right):\sqrt x \end{array}$

$\begin{array}{l}A = \left( {\sqrt x  + 2 + \sqrt x  - 2} \right).\dfrac{1}{{\sqrt x }}\\A = 2\sqrt x .\dfrac{1}{{\sqrt x }} = 2\end{array}$

Vậy với $x > 0,\,\,x \ne 4$ thì $A = 2$.

Câu 4 (1,75 điểm):

Phương pháp:

1) + Gọi vận tốc của Mai khi đi học bằng xe đạp là $x\,\,\left( {km/h} \right)\,\,\left( {x > 0} \right)$.

+ Tính được thời gian Mai đi xe đạp và đi xe máy hết quãng đường 3 km

+ Từ giả thiết cùng một thời điểm khởi hành như mọi ngày nhưng Mai đã đến trường sớm hơn 10 phút nên ta có phương trình ẩn $x$

+ Giải phương trình, đối chiếu điều kiện và kết luân.

2) Khối nón có chiều cao $h$ bán kính đáy là $r$ thì thể tích khối nón được tính theo công thức $V = \dfrac{1}{3}\pi {R^2}h$

Cách giải:

1) Gọi vận tốc của Mai khi đi học bằng xe đạp là $x\,\,\left( {km/h} \right)\,\,\left( {x > 0} \right)$.

Thời gian Mai đi xe đạp hết quãng đường 3km là $\dfrac{3}{x}\,\,\left( h \right)$.

Hôm nay, Mẹ chở Mai đến trường bằng xe máy với vận tốc là $x + 24\,\,\left( {km/h} \right)$.

Thời gian đi xe máy hết quãng đường 3km là $\dfrac{3}{{x + 24}}\,\,\left( h \right)$.

Vì cùng một thời điểm khởi hành như mọi ngày nhưng Mai đã đến trường sớm hơn 10 phút = $\dfrac{1}{6}h$ nên ta có phương trình:

$\begin{array}{l}\,\,\,\,\,\,\,\dfrac{3}{x} - \dfrac{3}{{x + 24}} = \dfrac{1}{6}\\ \Leftrightarrow 18\left( {x + 24} \right) - 18x = x\left( {x + 24} \right)\\ \Leftrightarrow {x^2} + 24x - 432 = 0\end{array}$

Ta có $\Delta ' = {12^2} + 432 = 576 > 0$ nên phương trình có 2 nghiệm phân biệt $\left[ \begin{array}{l}x =  - 12 + \sqrt {576}  = 12\,\,\,\,\,\,\left( {tm} \right)\\x =  - 12 - \sqrt {576}  =  - 36\,\,\left( {ktm} \right)\end{array} \right.$.

Vậy vận tốc của Mai khi đi học bằng xe đạp là $12\,\,km/h$.

2) Hình nón được tạo thành khi quay $\Delta ABC$ một vòng quanh cạnh $AC$ cố định có đường cao $h = AC = 2a$ và bán kính đường tròn đáy $R = AB = a$.

Vậy thể tích khối nón tạo thành là $V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi .{a^2}.2a = \dfrac{{2\pi {a^3}}}{3}$.

Câu 5 (3,0 điểm):

Phương pháp:

1) Vận dụng dấu hiệu nhận biết: Tứ giác có hai đỉnh kề cùng nhìn một cạnh dưới các góc bằng ${90^0}$ là tứ giác nội tiếp.

2) Chứng minh: $\angle IEH = \angle BHD$ và $\angle OEB = \angle OBE$$\Rightarrow \angle OEI = \angle BHD + \angle DBH$

Mặt khác có: $\angle OEI = {90^0}$

Vậy $IE$ là tiếp tuyến của đường tròn $\left( O \right)$ tại $E$.

3) Ta sẽ chứng minh $AD.DH = DI.DK\,\,\,\left( 1 \right)$ và $AD.DH = DB.DC\,\,\,\left( 2 \right)$

Từ (1) và (2) $\Rightarrow \dfrac{{DI}}{{DC}} = \dfrac{{DB}}{{DK}}$.

Chứng minh được $\Delta BDK \sim \Delta IDC\,\,\left( {c.g.c} \right)$$\Rightarrow \angle DBK = \angle DIC$ (2 góc tương ứng).

$\Rightarrow BK \bot IC$; $BM \bot IC$

Vậy $B,K,M$ thẳng hàng (đpcm).

Cách giải:

1) Tứ giác $BFEC$ có: $\angle BFC = \angle BEC = {90^0}\,\,\left( {gt} \right)$

Nên tứ giác $BFEC$ nội tiếp đường tròn đường kính $BC$ (Tứ giác có hai đỉnh kề cùng nhìn một cạnh dưới các góc bằng ${90^0}$).

Gọi $O$ là trung điểm của $BC$ $\Rightarrow O$ là tâm đường tròn ngoại tiếp tứ giác $BFEC$.

2) Tam giác $AEH$ vuông tại $E$ có $I$ là trung điểm của cạnh $AH$ nên $IE = \dfrac{1}{2}AH = IH$ (định lí đường trung tuyến trong tam giác vuông).

Suy ra $\Delta IEH$ cân tại $I$$\Rightarrow \angle IHE = \angle IEH$( tính chất tam giác cân)

Mặt khác $\angle BHD = \angle IHE$( hai góc đối đỉnh) $\Rightarrow \angle IEH = \angle BHD$  (1)

Tam giác $OBE$ có $OB = OE$ suy ra $\Delta OBE$ cân tại $O$

$\Rightarrow \angle OEB = \angle OBE$( tính chất tam giác cân)          (2)

Cộng vế theo vế của (1) và (2) ta có:

$\begin{array}{l}\angle IEH + \angle OEB = \angle BHD + \angle OBE\\ \Rightarrow \angle OEI = \angle BHD + \angle DBH\end{array}$

Mà  $\angle BHD + \angle DBH = {90^0}$( tam giác $BHD$ vuông tại $D$) $\Rightarrow \angle OEI = {90^0}$ hay $EI \bot OE$.

Vậy $IE$ là tiếp tuyến của đường tròn $\left( O \right)$ tại $E$.

3) Xét tứ giác $CDHE$ có $\angle CDH + \angle CEH = {90^0} + {90^0} = {180^0}$ nên $CDHE$ là tứ giác nội tiếp (dhnb).

$\Rightarrow \angle EDH = \angle ECH$ (2 góc nội tiếp cùng chắn cung $EH$).

Mà $\angle ECH = \angle IEF$ (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung $EF$).

$\Rightarrow \angle EDH = \angle IEF$.

Xét $\Delta IEK$ và $\Delta IDE$ có:

$\angle DIE$ chung;

$\angle EDH = \angle IEF\,\,\left( {cmt} \right) \Rightarrow \angle IEK = \angle IDE$;

$\Rightarrow \Delta IEK \sim \Delta IDE\,\,\left( {g.g} \right)$

$\Rightarrow \frac{{IE}}{{ID}} = \frac{{IK}}{{IE}} \Rightarrow I{E^2} = ID.IK$ (2 cạnh tương ứng). Mà $IE = IA \Rightarrow I{A^2} = ID.IK$  (*).

Ta sẽ chứng minh $AD.DH = DI.DK\,\,\,\left( 1 \right)$.

$\begin{array}{l} \Leftrightarrow \left( {DI + IA} \right).\left( {DI - IH} \right) = DI.DK\\ \Leftrightarrow \left( {DI + IA} \right).\left( {DI - IA} \right) = DI.DK\,\,\left( {do\,\,IH = IA} \right)\\ \Leftrightarrow D{I^2} - I{A^2} = DI.\left( {DI - IK} \right)\\ \Leftrightarrow I{A^2} = DI.IK\,\,\left( {dựa\,\,vào\,\,\left( * \right)} \right)\end{array}$

Lại có $\Delta ADC \sim \Delta BDH\,\,\left( {g.g} \right)$ $\Rightarrow \frac{{AD}}{{BD}} = \frac{{DC}}{{DH}} \Rightarrow AD.DH = DB.DC\,\,\,\left( 2 \right)$

Từ (1) và (2) $\Rightarrow DI.DK = DB.DC \Rightarrow \frac{{DI}}{{DC}} = \frac{{DB}}{{DK}}$.

Xét $\Delta BDK$ và $\Delta IDC$ có: $\angle DBI = \angle IDC = {90^0};\,\,\frac{{DI}}{{DC}} = \frac{{DB}}{{DK}}\,\,\left( {cmt} \right)$.

$\Rightarrow \Delta BDK \sim \Delta IDC\,\,\left( {c.g.c} \right)$ $\Rightarrow \angle DBK = \angle DIC$ (2 góc tương ứng).

Mà $\angle DIC + \angle DCI = {90^0} \Rightarrow \angle DBK + \angle DCI = {90^0}$ $\Rightarrow BK \bot IC$.

Mà $\angle BMC = {90^0}$ (góc nội tiếp chắn nửa đường tròn đường kính $BC$) $\Rightarrow BM \bot IC$.

Vậy $B,K,M$ thẳng hàng (đpcm).