Đề thi vào 10 môn Toán Tây Ninh năm 2019

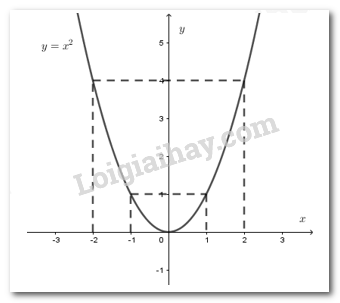
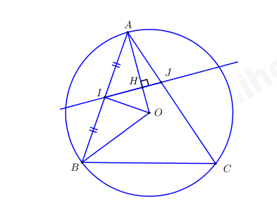
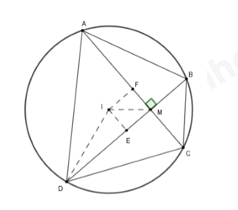
Đề bài

Câu 1 (1,0 điểm): Tính giá trị các biểu thức sau: $T = \sqrt 4  + \sqrt {25}  - \sqrt 9$

Câu 2 (1,0 điểm): Tìm $m$ để đồ thị hàm số $y = \left( {2m + 1} \right){x^2}$ đi qua điểm $A\left( {1;5} \right)$.

Câu 3 (1,0 điểm): Giải phương trình ${x^2} - x - 6 = 0$

Câu 4 (VD) (1,0 điểm): Vẽ đồ thị hàm số $y = {x^2}.$

Câu 5 (VD) (1,0 điểm): Tìm tọa độ giao điểm của đường thẳng ${d_1}:\,y = 2x + 1$ và đường thẳng ${d_2}:y = x + 3.$

Câu 6 (VD) (1,0 điểm) : Cho tam giác $ABC$ vuông cân tại $A$ có đường trung tuyến $BM$ ($M \in AC).$ Biết $AB = 2a.$ Tính theo $a$ độ dài $AC,\,AM$và $BM.$

Câu 7 (1 điểm):  Hai ô tô khởi hành cùng một lúc đi từ $A$ đến $B$. Vận tốc của ô tô thứ nhất lớn hơn vận tốc của ô tô thứ hai là $10km/h$ nên ô tô thứ nhất đến $B$ trước ô tô thứ hai $\dfrac{1}{2}$ giờ. Tính vạn tốc của mỗi ô tô. Biết rằng quãng đường $AB$ dài $150km.$ 

Câu 8 (1 điểm): Tìm các giá trị nguyên của m để phương trình ${x^2} - 4x + m + 1 = 0$ có hai nghiệm phân biệt ${x_1}$  và ${x_2}$  thỏa mãn $x_1^3 + x_2^3 < 100.$

Câu 9 (1 điểm):  Cho tam giác $ABC$ có ba góc nhọn và nội tiếp đường tròn tâm $O.$ Gọi $I$ là trung điểm của $AB,$ đường thẳng qua $I$ vuông góc với $AO$ và cắt cạnh $AC$ tại$J.$ Chứng minh bốn điểm $B,\,\,C,\,\,J,\,\,I$ cùng thuộc một đường tròn.

Câu 10 (1 điểm):  Cho đường tròn $\left( C \right)$ có tâm $I$ và có bán kính $R = 2a.$ Xét điểm $M$ thay đổi sao cho $IM = a.$ Hai dây $AC,\,\,BD$ đi qua điểm $M$  và vuông góc với nhau $\left( {A,\,\,B,\,\,C,\,\,D \in \left( C \right)} \right).$ Tìm giá trị lớn nhất của diện tích tứ giác $ABCD.$

Lời giải

Câu 1 (TH):

Phương pháp:

Khai căn bậc hai của một số.  $\sqrt {{A^2}}  = \left| A \right| = \left\{ \begin{array}{l}A,\,\,khi\,\,\,A \ge 0\\ - A,\,\,khi\,\,A < 0\end{array} \right.$

Cách giải:

Ta có: $T = \sqrt 4  + \sqrt {25}  - \sqrt 9  = 2 + 5 - 3 = 4$

Câu 2 (TH)

Phương pháp:

Thay tọa độ điểm A vào hàm số $y = \left( {2m + 1} \right){x^2}$, ta tìm được $m$ .

Cách giải:

Vì đồ thị hàm số $y = \left( {2m + 1} \right){x^2}$ đi qua điểm $A\left( {1;5} \right)$nên ta có:

$\begin{array}{l}5 = \left( {2m + 1} \right){.1^2}\\ \Rightarrow 5 = 2m + 1\\ \Rightarrow m = 2\end{array}$

Vậy với $m = 2$ đồ thị hàm số $y = \left( {2m + 1} \right){x^2}$ đi qua điểm $A\left( {1;5} \right)$

Câu 3 (VD)

Phương pháp:

Giải phương trình bậc hai một ẩn.

Cách giải:

${x^2} - x - 6 = 0\,\,\,\left( 1 \right) & ;\,\,\,a = 1;b =  - 1;c =  - 6$

Ta có: $\Delta  = {\left( { - 1} \right)^2} - 4.1.\left( { - 6} \right) = 25\,\, > 0\, \Rightarrow \sqrt \Delta   = 5$

$\Rightarrow$ Phương trình $\left( 1 \right)$ luôn có hai nghiệm phân biệt ${x_1},\,{x_2}$

$\begin{array}{l}{x_1} = \dfrac{{ - b + \sqrt \Delta  }}{{2.a}} = \dfrac{{1 + 5}}{2} = 3\\{x_2} = \dfrac{{ - b - \sqrt \Delta  }}{{2.a}} = \dfrac{{1 - 5}}{2} =  - 2\end{array}$

Vậy tập nghiệm của phương trình là : $S = \left\{ { - 2;3} \right\}$

Câu 4 (VD)

Phương pháp:

Lập bảng giá trị rồi vẽ đồ thị hàm số.

Cách giải:

Ta có bảng giá trị sau:

Vậy đồ thị hàm số $y = {x^2}$ là Parabol đi qua $5$ điểm có tọa độ $\left( { - 2;4} \right),\left( { - 1;1} \right),\left( {0;0} \right),\left( {1;1} \right),\left( {2;4} \right)$

Câu 5 (VD)

Phương pháp:

Cách 1: Giải phương trình hoành độ giao điểm.

Cách 2 : Giải hệ phương trình bao gồm 2 phương trình đường thẳng.

Cách giải:

Cách 1:

Phương trình hoành độ giao điểm của ${d_1},\,{d_2}$ là: $2x + 1 = x + 3 \Leftrightarrow 2x - x = 3 - 1 \Leftrightarrow x = 2$

Thay $x = 2$ vào d₂ ta có: $y = x + 3 = 2 + 3 = 5$.

Vậy $A\left( {2;5} \right)$ là giao điểm của hai đường thẳng.

Cách 2:

Gọi $A\left( {x;y} \right)$ là giao điểm của ${d_1}$ và ${d_2}$.

Tọa độ của $A$ là nghiệm của hệ phương trình: $\left\{ \begin{array}{l}y = 2x + 1\\y = x + 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - y =  - 1\\x - y =  - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\x - y =  - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 5\end{array} \right.$.

Vậy $A\left( {2;5} \right)$.

Câu 6 (VD)

Phương pháp :

+ Tam giác vuông cân có hai cạnh  góc vuông bằng nhau.

+ Tính chất đường trung tuyến.

+ Định lý py-ta-go trong tam giác.

Cách giải :

Câu 7 (VD)

Phương pháp:

Giải bài toán bằng cách lập phương trình

Bước 1: Đặt ẩn và tìm điều kiện của ẩn

Bước 2: Lập phương trình

Bước 3: Giải phương trình, so sánh các giá trị tìm được với điều kiện ở bước 1 để tìm các giá trị thỏa mãn sau đó kết luận.

Cách giải:

Gọi vận tốc của ô tô thứ hai là $x\,\,\,\left( {km/h} \right)\,\,\,\left( {x > 0} \right)$.

Vì vận tốc của ô tô thứ nhất lớn hơn vận tốc của ô tô thứ hai là $10\,km/h$ nên vận tốc của ô tô thứ nhất là $\left( {x + 10} \right)\,\,\,\,\left( {km/h} \right)$.

Thời gian ô tô thứ nhất đi hết quãng đường $AB$ là $\dfrac{{150}}{{x + 10}}\,\,\,\,\left( h \right)$.

Thời gian ô tô thứ hai đi hết quãng đường $AB$ là $\dfrac{{150}}{x}\,\,\,\left( h \right)$.

Vì ô tô thứ nhất đến B trước ô tô thứ hai là $\dfrac{1}{2}$ giờ nên ta có phương trình $\dfrac{{150}}{{x + 10}} + \dfrac{1}{2} = \dfrac{{150}}{x}$

$\Rightarrow 300x + x\left( {x + 10} \right) = 300\left( {x + 10} \right)$

$\Leftrightarrow 300x + {x^2} + 10x = 300x + 3000$

$\begin{array}{l} \Leftrightarrow {x^2} + 10x - 3000 = 0\\ \Leftrightarrow {x^2} - 50x + 60x - 3000 = 0\end{array}$

$\begin{array}{l} \Leftrightarrow x\left( {x - 50} \right) + 60\left( {x - 50} \right) = 0\\ \Leftrightarrow \left( {x + 60} \right)\left( {x - 50} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 60 = 0\\x - 50 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - 60\,\,\,\left( {ktm} \right)\\x = 50\,\,\,\,\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}$

Vậy vận tốc ô tô thứ hai là $50\,km/h$ và vận tốc  ô tô thứ nhất là $50 + 10 = 60\,km/h$.

Câu 8 (VD)

Phương pháp:

Phương trình $a{x^2} + bx + c = 0$ có hai nghiệm phân biệt $\Leftrightarrow \Delta  > 0.$

Áp dụng hệ thức Vi-et và biến đổi hệ thức bài cho $x_1^3 + x_2^3 = \left( {{x_1} + {x_2}} \right)\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 3{x_1}{x_2}} \right]$ để tìm giá trị $m$ thỏa mãn bài toán.

Cách giải:

${x^2} - 4x + m + 1 = 0$

 Ta có: $a = 1;b =  - 4;c = m + 1$

$\Rightarrow \Delta ' = {\left( { - 2} \right)^2} - m - 1 = 3 - m$

Phương trình có hai nghiệm phân biệt $\Leftrightarrow \Delta ' > 0 \Leftrightarrow 3 - m > 0 \Leftrightarrow m < 3$

Áp dụng hệ thức Vi-et cho phương trình ta có:  $\left\{ \begin{array}{l}{x_1} + {x_2} = 4\\{x_1}{x_2} = m + 1\end{array} \right.$

Theo đề bài ta có:

 $\begin{array}{l}\,\,\,\,\,\,\,\,x_1^3 + x_2^3 < 100\\ \Leftrightarrow \left( {{x_1} + {x_2}} \right)\left( {x_1^2 - {x_1}{x_2} + x_2^2} \right) < 100\\ \Leftrightarrow \left( {{x_1} + {x_2}} \right)\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 3{x_1}{x_2}} \right] < 100\\ \Leftrightarrow 4.\left[ {16 - 3\left( {m + 1} \right)} \right] < 100\\ \Leftrightarrow 16 - 3m - 3 < 25\\ \Leftrightarrow  - 3m < 12 \Leftrightarrow m >  - 4\end{array}$

Kết hợp với điều kiện $m < 3$  và $m$  nguyên ta có: $\left\{ \begin{array}{l} - 4 < m < 3\\m \in \mathbb{Z}\end{array} \right. \Rightarrow m \in \left\{ { - 3; - 2; - 1;\,\,0;\,\,1;\,\,2} \right\}$ 

Vậy $m \in \left\{ { - 3; - 2; - 1;\,\,0;\,\,1;\,\,2} \right\}$ thỏa mãn yêu cầu bài toán.

Chú ý khi giải: HS chú khi giải xong nhớ kết hợp điều kiện của $m$ và điều kiện $m \in \mathbb{Z}.$

Câu 9 (VD)

Phương pháp:

Sử dụng các tính chất về số đo góc nội tiếp và góc ở tâm cùng chắn một cung để chứng minh các góc tường ứng bằng nhau.

Chứng minh tứ giác $BIJC$ là tứ giác nội tiếp nhờ dấu hiệu nhận biết.

Cách giải:

Gọi $H = IJ \cap OA$.

Do $I$ là trung điểm của $AB \Rightarrow OI \bot AB$ tại $I$ (quan hệ vuông góc giữa đường kính và dây cung).

$\Rightarrow \Delta OAI$ vuông tại $I$.

Xét tam giác vuông $OAI$ có: $\angle IOA + \angle OAI = {90^0}$.

Xét tam giác vuông $IAH$ có: $\angle HIA + \angle HAI = {90^0} \Rightarrow \angle JIA + \angle OAI = {90^0}$.

$\Rightarrow \angle IOA = \angle JIA$ (1).

Do tam giác $OAB$ cân tại $O\,\,\left( {OA = OB} \right) \Rightarrow$ Trung tuyến $OI$  đồng thời là phân giác.

$\Rightarrow \angle IOA = \dfrac{1}{2}\angle AOB$.

Mà $\angle ACB = \dfrac{1}{2}\angle AOB$ (tính chất góc nội tiếp và góc ở tâm cùng chắn cung $AB$).

$\Rightarrow \angle IOA = \angle ACB = \angle JCB$ (2).

Từ $\left( 1 \right),\,\left( 2 \right) \Rightarrow \angle JIA = \angle JCB \Rightarrow$ Tứ giác $BCJI$ là tứ giác nội tiếp (Tứ giác có góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện).

Vậy bốn điểm $B,\,\,C,\,\,J$ và $I$ cùng thuộc 1 đường tròn.

Câu 10 (VDC):

Phương pháp:

+) Sử dụng công thức tính diện tích tứ giác có 2 đường chéo vuông góc: $S = \dfrac{1}{2}AC.BD$.

+) Áp dụng BĐT Cô-si.

+) Chứng minh $A{C^2} + B{D^2}$ không đổi.

+) Tìm điều kiện để dấu “=” xảy ra.

Cách giải:

Tứ giác $ABCD$ có hai đường chéo $AC \bot BD$ $\Rightarrow {S_{ABCD}} = \dfrac{1}{2}AC.BD \le \dfrac{{A{C^2} + B{D^2}}}{4}$

Kẻ $IE \bot AC\left( {E \in AC} \right),IF \bot BD\left( {F \in BD} \right)$

$AC = 2AF = 2\sqrt {I{A^2} - I{F^2}}  = 2\sqrt {4{a^2} - I{F^2}}$

$BD = 2DE = 2\sqrt {I{D^2} - I{E^2}}  = 2\sqrt {4{a^2} - I{E^2}}$

$\Rightarrow A{C^2} + B{D^2} = 4\left( {4{a^2} - I{F^2}} \right) + 4\left( {4{a^2} - I{E^2}} \right)$ $= 32{a^2} - 4\left( {I{E^2} + I{F^2}} \right)$.

Xét tứ giác $IEMF$ có $\angle IEM = \angle IFM = \angle EMF = {90^0} \Rightarrow IEMF$ là hình chữ nhật (tứ giác có ba góc vuông)

$\Rightarrow IF = EM \Rightarrow I{E^2} + I{F^2} = I{M^2} = {a^2}$

$\Rightarrow A{C^2} + B{D^2} = 32{a^2} - 4{a^2} = 28{a^2}$

$\Rightarrow {S_{ABCD}} \le \dfrac{{28{a^2}}}{4} = 7{a^2}$.

Dấu “=” xảy ra $\Leftrightarrow AC = BD$.

Vậy ${S_{ABCD}}$ đạt GTLN bằng $7{a^2}$ khi $AC = BD$.