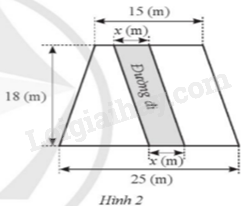
Giải bài 17 trang 42 sách bài tập toán 9 - Cánh diều tập 1Cho một khu đất có dạng hình thang với đáy nhỏ 15 (m), đáy lớn 25 (m), chiều cao 18 (m). Bác Lâm muốn dành ra một mảnh vườn có dạng hình bình hành với cạnh đáy x (m), chiều cao 18 (m) như Hình 2(0 < x < 15). Tìm giá trị lớn nhất của x để diện tích của phần đất còn lại không dưới 270 m2. Đề bài Cho một khu đất có dạng hình thang với đáy nhỏ 15 (m), đáy lớn 25 (m), chiều cao 18 (m). Bác Lâm muốn dành ra một mảnh vườn có dạng hình bình hành với cạnh đáy x (m), chiều cao 18 (m) như Hình 2(0 < x < 15). Tìm giá trị lớn nhất của x để diện tích của phần đất còn lại không dưới 270 m2.
Phương pháp giải - Xem chi tiết Bước 1: Tính diện tích khu đất hình thang. Bước 2: Tính diện tích khu đất hình bình hành. Bước 3: Diện tích còn lại = diện tích hình thang – diện tích hình bình hành. Bước 4: Lập và giải bất phương trình. Lời giải chi tiết Diện tích khu đất hình thang là \(\frac{{\left( {15 + 25} \right).18}}{2} = 360{m^2}.\) Diện tích khu đất hình bình hành là \(18{x^{}}{m^2}.\) Vì phần đất còn lại không dưới 270 m2 nên ta có: \(\begin{array}{l}360 - 18x \ge 270\\18x \le 90\\x \le 5\end{array}\) Vậy giá trị lớn nhất của x là 5.
|