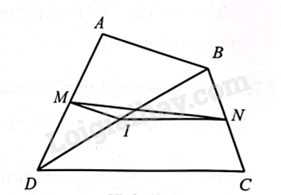
Giải bài 20 trang 66 sách bài tập toán 8 – Cánh diềuCho tứ giác \(ABCD\) có \(M,N\) lần lượt là trung điểm của \(AD,BC\). Chứng minh: \(MN \le \frac{{AB + DC}}{2}\). Dấu đẳng thức xảy ra khi nào? Đề bài Cho tứ giác \(ABCD\) có \(M,N\) lần lượt là trung điểm của \(AD,BC\). Chứng minh: \(MN \le \frac{{AB + DC}}{2}\). Dấu đẳng thức xảy ra khi nào? Phương pháp giải - Xem chi tiết Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh tam giác đó. Tính chất: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh đó. Lời giải chi tiết
Lấy \(I\) là trung điểm của \(BD\). Khi đó, ta có \(MI,NI\) lần lượt là các đường trung bình của tam giác \(ABD\) và \(BDC\) nên \(MI = \frac{{AB}}{2},NI = \frac{{CD}}{2}\). Do đó \(MI + NI = \frac{{AB + CD}}{2}\) (1) - Nếu \(I\) không thuộc \(MN\) ta có \(MN < MI + NI\) (bất đẳng thức tam giác). - Nếu \(I\) thuộc \(MN\) ta có \(MN = MI + NI\). Tức là, ta luôn có \(MN \le MI + NI\) (2). Từ (1) và (2) suy ra \(MN \le \frac{{AB + CD}}{2}\). Dấu đẳng thức xảy ra khi \(I\) thuộc \(MN\), khi đó \(AB//CD\).
|