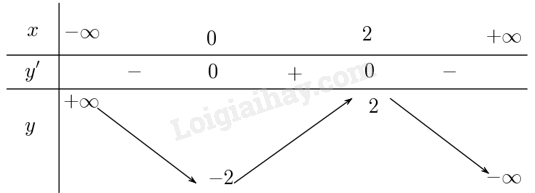
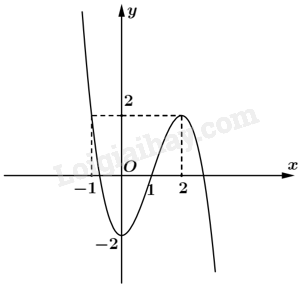
Giải bài 23 trang 51 sách bài tập toán 12 - Kết nối tri thứca) Khảo sát sự biến thiên và vẽ đồ thị hàm số (y = - {x^3} + 3{x^2} - 2). b) Tìm điều kiện của tham số m để phương trình ( - {x^3} + 3{x^2} + 5 - m = 0) có ba nghiệm phân biệt. c) Tìm điểm thuộc đồ thị hàm số mà tiếp tuyến với đồ thị tại điểm đó có hệ số góc lớn nhất. Đề bài a) Khảo sát sự biến thiên và vẽ đồ thị hàm số \(y = - {x^3} + 3{x^2} - 2\). b) Tìm điều kiện của tham số m để phương trình \( - {x^3} + 3{x^2} + 5 - m = 0\) có ba nghiệm phân biệt. c) Tìm điểm thuộc đồ thị hàm số mà tiếp tuyến với đồ thị tại điểm đó có hệ số góc lớn nhất. Phương pháp giải - Xem chi tiết Ý a: Tìm tập xác định, xét dấu đạo hàm, tính các giới hạn tại vô cực, tìm tiệm cận (nếu có), lập bảng biến thiên và vẽ đồ thị. Ý b: Xét phương trình, cô lập m. Xét sự biến thiên của hàm số ở vế không chứa m, tìm m để đường thẳng chỉ phụ thuộc m đã cô lập cắt đồ thị đó tại ba điểm phân biệt. Ý c: Điểm thuộc đồ thị nên có thể biểu diễn nó theo một tham số. Tính giá trị đạo hàm tại điểm, tìm giá trị lớn nhất của đạo hàm từ đó tìm được tham số và suy ra điểm. Lời giải chi tiết a) Tập xác định: \(\mathbb{R}\). Sự biến thiên: Ta có \(y' = - 3{x^2} + 6x\) suy ra \(y' = 0 \Leftrightarrow - 3{x^2} + 6x = 0 \Leftrightarrow x = 0\) hoặc \(x = 2\). Hàm số đồng biến trên \(\left( {0;2} \right)\) và nghịch biến trên từng khoảng \(\left( { - \infty ;0} \right)\), \(\left( {2; + \infty } \right)\). Hàm số đạt cực đại tại \(x = 2\) và \({y_{CĐ}} = 2\). Hàm số đạt cực tiểu tại \(x = 0\) và \({y_{CT}} = - 2\). Giới hạn tại vô cực \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \), \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty \). Ta có bảng biến thiên: Đồ thị hàm số: b) Ta có \( - {x^3} + 3{x^2} - 2 = 3 - m\). Suy ra phương trình có ba nghiệm phân biệt khi và chỉ khi đường thẳng \(y = 3 - m\) cắt đồ thị \(y = - {x^3} + 3{x^2} - 2\) tại ba điểm phân biệt. Điều này tương đương với \(2 < 3 - m < 2 \Leftrightarrow 1 < m < 5\). c) Ta có \(y' = - 3{x^2} + 6x = - 3{\left( {x - 1} \right)^2} + 3 \le 3,{\rm{ }}\forall x\). Vậy tiếp tuyến có hệ số góc lớn nhất bằng 3 tại \(x = 1\). Do đó điểm cần tìm có tọa độ \(\left( {1;0} \right)\).
|