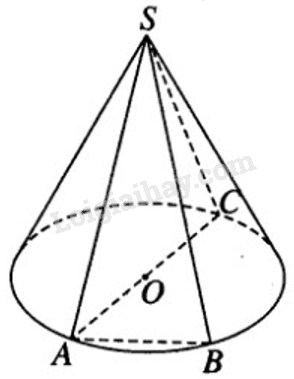
Bài 2.5 trang 47 SBT hình học 12Giải bài 2.5 trang 47 sách bài tập hình học 12. Chứng minh rằng trong một khối nón tròn xoay, góc ở đỉnh là góc lớn nhất trong số các góc được tạo nên bởi hai đường sinh của khối nón đó. Đề bài Chứng minh rằng trong một khối nón tròn xoay, góc ở đỉnh là góc lớn nhất trong số các góc được tạo nên bởi hai đường sinh của khối nón đó. Phương pháp giải - Xem chi tiết Sử dụng tính chất góc và cạnh đối diện trong tam giác. Lời giải chi tiết
Xét hai đường sinh \(SA , SB\) tùy ý của hình nón. Vẽ đường kính \(AC\) của đường tròn đáy. Ta có góc \(\widehat {ASC}\) là góc ở đỉnh của hình nón. Hai tam giác \(ASC\) và \(ASB\) có hai cặp cạnh bằng nhau vì chúng cùng là đường sinh của hình nón. Ta có cạnh \(AC \ge AB\) nên \(\widehat {{\rm{AS}}C} \ge \widehat {ASB}\). Đó là điều cần chứng minh. HocTot.XYZ
|