Bài 2.9 trang 47 SBT hình học 12Giải bài 2.9 trang 47 sách bài tập hình học 12. Một khối trụ có bán kính đáy bằng r và chiều cao bằng... Đề bài Một khối trụ có bán kính đáy bằng r và chiều cao bằng \(r\sqrt 3 \). Gọi A và B là hai điểm trên hai đường tròn đáy sao cho góc được tạo thành giữa đường thẳng AB và trục của khối trụ bằng 300. a) Tính diện tích của thiết diện qua AB và song song với trục của khối trụ. b) Tính góc giữa hai bán kính đáy qua A và B. c) Xác định và tính độ dài đoạn vuông góc chung của AB và trục của khối trụ. Phương pháp giải - Xem chi tiết a) Xác định thiết diện và tính diện tích. b) Xác định góc giữa hai bán kính và tính toán dựa vào các kiến thức hình học đã biết. c) Xác định đoạn vuông góc chung của AB và trục khối trụ, từ đó tính độ dài. Lời giải chi tiết
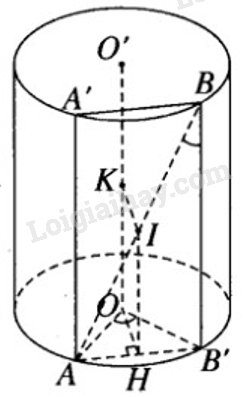
a) Từ A và B dựng các đường sinh AA’ và BB’ ta có thiết diện qua AB và song song với trục là hình chữ nhật AA’BB’. Vì OO'//BB' nên góc giữa AB và OO' là góc giữa AB và BB' hay \(\displaystyle \widehat {ABB'}\). Do đó, \(\displaystyle \widehat {ABB'} = {30^0}\). Vậy \(\displaystyle AB' = BB'\tan {30^0} = r\sqrt 3 .{1 \over {\sqrt 3 }} = r\) Do đó diện tích tứ giác AA’BB’ là \(\displaystyle {S_{{\rm{AA}}'BB'}} = AB'.BB' = r.r\sqrt 3 = {r^2}\sqrt 3 \) b) Bán kính đáy qua A là OA; bán kính đáy qua B là O'B. Vì O'B//OB' nên góc giữa OA và O’B là góc giữa OA và OB' hay \(\displaystyle \widehat {AOB'}\) Vì AB’ = r nên AOB’ là tam giác đều, do đó \(\displaystyle \widehat {AOB}' = {60^0}\) c) Mặt phẳng (ABB’) chứa AB và song song với trục OO’ của hình trụ. Gọi H là trung điểm của AB’. Ta có \(\displaystyle OH \bot (ABB')\). Đường thẳng qua H song song với OO’ cắt AB tại I. Dựng IK // HO cắt OO’ tại K. Ta có: \(OH \bot OO' \Rightarrow IK \bot OO'\) Lại có \(OH \bot \left( {ABB'} \right) \Rightarrow IK \bot \left( {ABB'} \right)\) \( \Rightarrow IK \bot AB\) Do đó IK là đoạn vuông góc chung của AB và OO'. Mà \(\displaystyle IK = HO = {{r\sqrt 3 } \over 2}\) nên \(d\left( {AB,OO'} \right) = \frac{{r\sqrt 3 }}{2}\) HocTot.XYZ
|