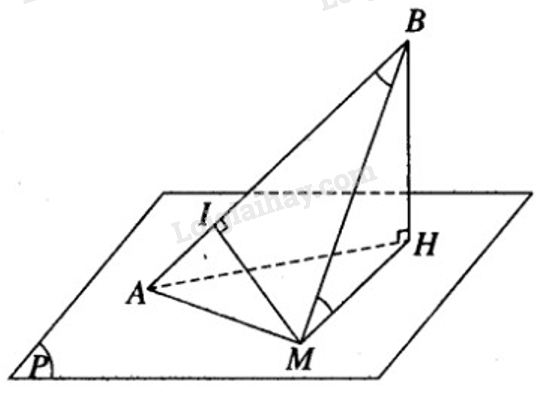
Bài 2.7 trang 47 SBT hình học 12Giải bài 2.7 trang 47 sách bài tạp hình học 12. Cho mặt phẳng (P). Gọi A là một điểm nằm trên (P) và B là một điểm nằm ngoài (P) sao cho hình chiếu H của B trên (P) không trùng với A. Đề bài Cho mặt phẳng (P). Gọi A là một điểm nằm trên (P) và B là một điểm nằm ngoài (P) sao cho hình chiếu H của B trên (P) không trùng với A. Một điểm M chạy trên mặt phẳng (P) sao cho góc \(\widehat {ABM} = \widehat {BMH}\) . Chứng minh rằng điểm M luôn luôn nằm trên một mặt trụ tròn xoay có trục là AB. Phương pháp giải - Xem chi tiết Gọi I là hình chiếu của M lên AB. Chứng minh MI=BH không đổi và suy ra khối trụ cần tìm. Lời giải chi tiết
Giả sử ta có điểm M thuộc mặt phẳng (P) thỏa mãn các điều kiện của giả thiết đã cho. Gọi I là hình chiếu vuông góc của M trên AB. Xét tam giác vuông BIM và MHB có: \(BM\) chung. \(\widehat B = \widehat M\) (giả thiết) Suy ra \(\Delta BIM = \Delta MHB\left( {c - h - g - n} \right)\) Do đó MI = BH không đổi hay M luôn cách AB một khoảng không đổi. Vậy điểm M luôn luôn nằm trên mặt trụ trục AB và có bán kính bằng BH. HocTot.XYZ
|