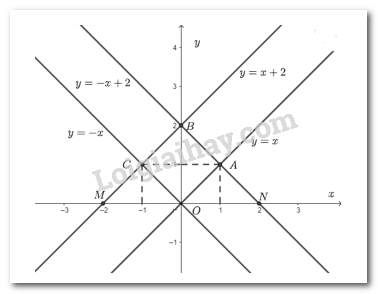
Giải Bài 3 trang 22 SGK Toán 8 tập 2 – Chân trời sáng tạo

a)

Vẽ đồ thị các hàm số sau đây trên cùng một mặt phẳng tọa độ:

$y = x$; $y = x + 2$; $y =  - x$; $y =  - x + 2$.

Phương pháp giải:

- Để vẽ đồ thị hàm số $y = ax$, ta thường thực hiện các bước sau:

Bước 1: Xác định một điểm $M$ trên đồ thị khác gốc tọa độ $O$, chẳng hạn $M\left( {1;a} \right)$.

Bước 2: Vẽ đường thẳng đi qua hai điểm $O$ và $M$. Đồ thị hàm số $y = ax$ là đường thẳng đi qua hai điểm $O$ và $M$.

- Để vẽ đồ thị hàm số $y = ax + b$ ta làm như sau:

Bước 1: Cho $x = 0 \Rightarrow y = b$ ta được điểm $A\left( {0;b} \right)$ trên trục $Oy$.

Cho $y = 0 \Rightarrow x = \dfrac{{ - b}}{a}$ ta được điểm $B\left( {\dfrac{{ - b}}{a};0} \right)$ trên $Ox$.

Bước 2: Vẽ đường thẳng đi qua hai điểm $A$ và $B$. Đồ thị của hàm số $y = ax + b$ là đường thẳng đi qua hai điểm $A$ và $B$.

- Đồ thị hàm số $y = ax + b$ là một đường thẳng và song song với đường thẳng $y = ax$.

Lời giải chi tiết:

- Vẽ đồ thị hàm số $y = x$

Cho $x = 1$ thì $y = 1$ suy ra đồ thị hàm số đi qua điểm $A\left( {1;1} \right)$.

Đồ thị hàm số $y = x$ là đường thẳng đi qua hai điểm $O\left( {0;0} \right)$ và $A\left( {1;1} \right)$.

- Vẽ đồ thị hàm số $y = x + 2$

Cho $x = 0$ thì $y = 2$ ta được điểm $B\left( {0;2} \right)$ trên trục $Oy$.

Cho $y = 0$ thì $x =  - 2$ ta được điểm $M\left( { - 2;0} \right)$ trên $Ox$.

Đồ thị hàm số$y = x + 2$ là đường thẳng đi qua hai điểm $B\left( {0;2} \right)$ và $M\left( { - 2;0} \right)$.

- Vẽ đồ thị hàm số $y =  - x$

Cho $x = -1$ thì $y =  1$ suy ra đồ thị hàm số đi qua điểm $C\left( {-1;1} \right)$.

Đồ thị hàm số $y =  - x$ là đường thẳng đi qua hai điểm $O\left( {0;0} \right)$ và $C\left( {- 1;1} \right)$.

- Vẽ đồ thị hàm số $y =  - x + 2$

Cho $x = 0$ thì $y = 2$ ta được điểm $B\left( {0;2} \right)$ trên trục $Oy$.

Cho $y = 0$ thì $x = 2$ ta được điểm $N\left( {2;0} \right)$ trên $Ox$.

Đồ thị hàm số $y =  - x + 2$ là đường thẳng đi qua hai điểm $B\left( {0;2} \right)$ và $N\left( {2;0} \right)$.

b)

Bốn đồ thị nói trên cắt nhau tại các điểm $O\left( {0;0} \right),A,B,C$. Tứ giác có bốn đỉnh $O;A;B;C$ là hình gì? Giải thích.

Phương pháp giải:

Tính độ dài các cạnh và góc của tứ giác.

Chú ý: Hình thoi có 1 góc vuông là hình vuông.

Lời giải chi tiết:

Vì đường thẳng $y = x$;$y = x + 2$ song song với nhau và $y =  - x$;$y =  - x + 2$ song song với nhau nên tứ giác $OABC$ là hình bình hành.

Lại có $OC;OA$ là đường chéo của hình vuông có độ dài cạnh là 1 nên $OC = OA$. Do đó, tứ giác $OABC$ là hình thoi.

Lại có $OC;OA$ là đường chéo của hình vuông nên cũng là đường phân giác. Do đó, $\widehat {COB} = \widehat {AOB} = 45^\circ  \Rightarrow \widehat {COA} = \widehat {COB} + \widehat {AOB} = 45^\circ  + 45^\circ  = 90^\circ$

Hình thoi $OABC$ có góc $\widehat {COA} = 90^\circ$ nên tứ giác $OABC$ là hình vuông.