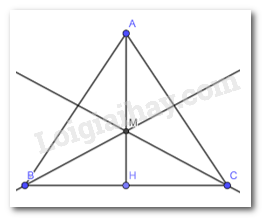
Giải bài 3 trang 82 SGK Toán 7 tập 2 - Chân trời sáng tạoCho tam giác ABC cân tại A. Tia phân giác của các góc B và C cắt nhau tại M. Tia AM cắt BC tại H. Chứng minh rằng H là trung điểm của BC Đề bài Cho tam giác ABC cân tại A. Tia phân giác của các góc B và C cắt nhau tại M. Tia AM cắt BC tại H. Chứng minh rằng H là trung điểm của BC Phương pháp giải - Xem chi tiết Chứng minh BH = CH thông qua 2 tam giác bằng nhau Lời giải chi tiết
Vì M là giao điểm của 2 phân giác góc B, C nên M là điểm giao của 3 phân giác trong tam giác ABC \( \Rightarrow \) AM cũng là phân giác của góc A (định lí về 3 phân giác cùng đi qua 1 điểm) \( \Rightarrow \widehat {BAH} = \widehat {CAH}\)(tính chất tia phân giác của 1 góc) Xét tam giác ABH và tam giác ACH có : AB = AC ( tam giác ABC cân tại A ) \(\widehat {BAH} = \widehat {CAH}\)(chứng minh trên) AH cạnh chung \( \Rightarrow \Delta ABH=\Delta ACH\) (c.g.c) \( \Rightarrow \) HB = HC (cạnh tương ứng) \( \Rightarrow \)H là trung điểm của BC
|