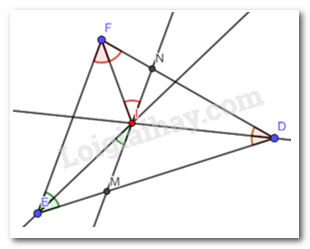
Giải bài 4 trang 82 SGK Toán 7 tập 2 - Chân trời sáng tạoCho tam giác DEF. Tia phân giác của góc D và E cắt nhau tại I. Qua I kẻ đường thẳng song song với EF, đường thằng này cắt DE tại M, cắt DF tại N. Chứng minh rằng ME + NF = MN. Đề bài Cho tam giác DEF. Tia phân giác của góc D và E cắt nhau tại I. Qua I kẻ đường thẳng song song với EF, đường thằng này cắt DE tại M, cắt DF tại N. Chứng minh rằng ME + NF = MN. Phương pháp giải - Xem chi tiết - Ta thấy MN = MI + NI - Nên ta sẽ chứng minh MI = ME, NI = NF qua các tam giác cân Lời giải chi tiết
Theo đề bài ta có MN song song với EF \( \Rightarrow \) \(\widehat {FEI} = \widehat {EIM}\)(2 góc so le trong) và \(\widehat {EFI} = \widehat {FIN}\)(2 góc so le trong) Xét có \(\widehat {FEI} = \widehat {EIM} = \widehat {IEM}\)(EI là phân giác góc E)cân tại M (2 góc đáy bằng nhau) \( \Rightarrow \) EM = IM (2 cạnh bên tam giác cân) (1) Xét có : \(\widehat {EFI} = \widehat {IFN} = \widehat {NIF}\)(FI là phân giác góc F) cân tại N (2 góc đáy bằng nhau) \( \Rightarrow \)FN = IN (2 cạnh bên tam giác cân) (2) Ta thấy MN = MI + NI (3) Từ (1); (2) và (3) \( \Rightarrow \) ME + NF = MN
|