Giải bài 3.23 trang 42 sách bài tập toán 8 - Kết nối tri thức với cuộc sốngChứng minh hình bình hành có hai đường cao xuất phát từ một đỉnh bằng nhau là một hình thoi. Đề bài Chứng minh hình bình hành có hai đường cao xuất phát từ một đỉnh bằng nhau là một hình thoi. Phương pháp giải - Xem chi tiết Sử dụng kiến thức về dấu hiệu nhận biết hình thoi để chứng minh: Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi. Lời giải chi tiết
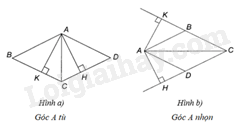
Xét hình bình hành ABCD có đường cao AH (H thuộc đường thẳng CD), và đường cao AK (K thuộc đường thẳng BC) thỏa mãn \(AH = AK\) Tam giác ACH và tam giác ACK có: \(\widehat {AHC} = \widehat {AKC} = {90^0}\), \(AH = AK\), cạnh AC chung Do đó, \(\Delta ACH = \Delta ACK\) (ch – cgv) Suy ra: \(\widehat {ACK} = \widehat {ACH}\) nên CA là tia phân giác góc BCD. Hình bình hành ABCD có CA là tia phân giác góc BCD nên ABCD là hình thoi.
|