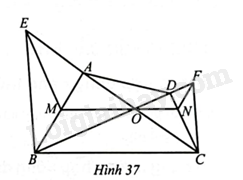
Giải bài 39 trang 75 sách bài tập toán 8 – Cánh diềuTrong Hình 37, cho (O) là giao điểm hai đường chéo (AC) và (BD) của tứ giác (ABCD). Kẻ một đường thẳng tùy ý đi qua (O) và cắt cạnh (AB) tại (M,CD) tại (N). Đề bài Trong Hình 37, cho \(O\) là giao điểm hai đường chéo \(AC\) và \(BD\) của tứ giác \(ABCD\). Kẻ một đường thẳng tùy ý đi qua \(O\) và cắt cạnh \(AB\) tại \(M,CD\) tại \(N\). Đường thẳng qua \(M\) song song với \(CD\) cắt \(AC\) tại \(E\) và đường thẳng qua \(N\) song song với \(AB\) cắt \(BD\) tại \(F\). Chứng minh: a) \(\Delta OBE\backsim \Delta OFC\); b) \(BE//CF\)
Phương pháp giải - Xem chi tiết Áp dụng trường hợp đồng dạng thứ hai của tam giác: cạnh – góc – cạnh Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng. Lời giải chi tiết a) Do \(MB//NF\) nên theo định lí Thales ta có \(\frac{{OB}}{{OF}} = \frac{{OM}}{{ON}}\) (1) Tương tự \(NC//ME = > \frac{{OE}}{{OC}} = \frac{{OM}}{{ON}}\) (2) Từ (1) và (2) ta có: \(\frac{{OB}}{{OF}} = \frac{{OE}}{{OC}}\). Mà \(\widehat {BOE} = \widehat {FOC}\) (hai góc đối đỉnh). Suy ra \(\Delta OBE\backsim \Delta OFC\) (c.g.c) b) Theo câu a, ta có \(\Delta OBE\backsim \Delta OFC\) nên \(\widehat {EBO} = \widehat {CFO}\). Mà hai góc \(\widehat {EBO}\) và \(\widehat {CFO}\) ở vị trí so le trong \( = > BE//CF\).  Chia sẻ Bình luận
Tham Gia Group Dành Cho Lớp 8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
