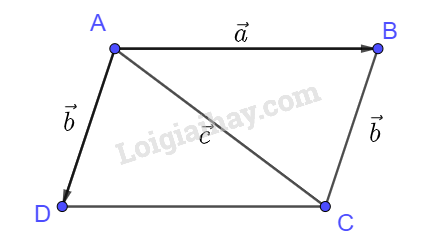
Giải bài 4 trang 103 sách bài tập toán 10 - Chân trời sáng tạo

Đề bài

Chứng minh rằng với hai vectơ không cùng phương $\overrightarrow a$ và $\overrightarrow b$, ta có:

   $\left| {\overrightarrow a } \right| - \left| {\overrightarrow b } \right| \le \left| {\overrightarrow a  + \overrightarrow b } \right| \le \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|$

Lời giải chi tiết

TH1: $\overrightarrow a  = \overrightarrow 0$

$\Rightarrow \left| {\overrightarrow a } \right| - \left| {\overrightarrow b } \right| = \left| {\overrightarrow a  + \overrightarrow b } \right| = \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = \left| {\overrightarrow b } \right|$

TH2: $\overrightarrow b  = \overrightarrow 0$

$\Rightarrow \left| {\overrightarrow a } \right| - \left| {\overrightarrow b } \right| = \left| {\overrightarrow a  + \overrightarrow b } \right| = \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = \left| {\overrightarrow a } \right|$

TH3: $\overrightarrow a  \ne \overrightarrow 0$ và $\overrightarrow b  \ne \overrightarrow 0$

Lấy A bất kì, vẽ $\overrightarrow {AB}  = \overrightarrow a ,\overrightarrow {AD}  = \overrightarrow b$. Dựng hình bình hành ABCD, đặt $\overrightarrow c  = \overrightarrow {AC}$

 Ta có: $\overrightarrow a  + \overrightarrow b  = \overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC}  = \overrightarrow c$

Xét tam giác ABC, theo bất đẳng thức tam giác ta có:

$AB - BC < AC < AB + BC$

Mà $\left| {\overrightarrow a } \right| = \left| {\overrightarrow {AB} } \right| = AB;\left| {\overrightarrow b } \right| = \left| {\overrightarrow {AD} } \right| = AD = BC;\left| {\overrightarrow c } \right| = \left| {\overrightarrow {AC} } \right| = AC;$

$\Rightarrow \left| {\overrightarrow a } \right| - \left| {\overrightarrow b } \right| < \left| {\overrightarrow a  + \overrightarrow b } \right| < \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|$

Vậy $\left| {\overrightarrow a } \right| - \left| {\overrightarrow b } \right| \le \left| {\overrightarrow a  + \overrightarrow b } \right| \le \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|$