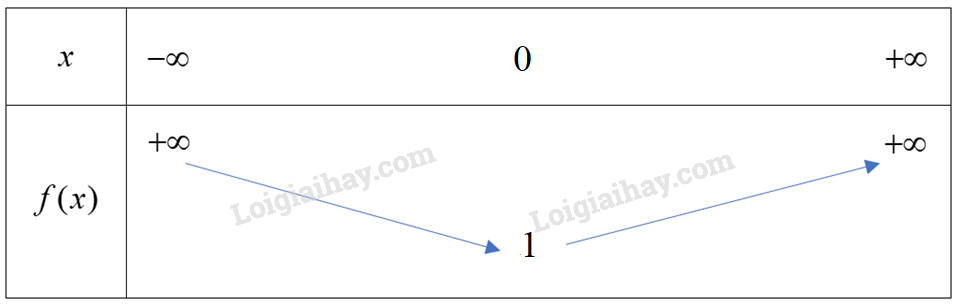
Giải bài 4 trang 56 SGK Toán 10 tập 1 – Chân trời sáng tạoCho hàm số bậc hai y = f(x) = ax^2 + bx + c có f(0) = 1,f(1) = 2,f(2) = 5. a) Hãy xác định giá trị của các hệ số a,b và c b) Xác định tập giá trị và khoảng biến thiên của hàm số. Đề bài Cho hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) có \(f(0) = 1,f(1) = 2,f(2) = 5.\) a) Hãy xác định giá trị của các hệ số \(a,b\) và \(c.\) b) Xác định tập giá trị và khoảng biến thiên của hàm số. Phương pháp giải - Xem chi tiết a) \(f(0) = a{.0^2} + b.0 + c = 1\), từ đó suy ra c. Tương tự, sử dụng giả thiết \(f(1) = 2,f(2) = 5,\)lập hệ phương trình 2 ẩn a, b. b) Tập giá trị \(T = \{ f(x)|x \in D\} \) với D là tập xác định của hàm số \(f(x).\) Với \(a = 1 > 0\): Lời giải chi tiết a) Ta có: \(f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.\) Lại có: \(f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2\) \(f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5\) Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\)(thỏa mãn điều kiện \(a \ne 0\)) Vậy hàm số bậc hai đó là \(y = f(x) = {x^2} + 1\) b) Tập giá trị \(T = \{ {x^2} + 1|x \in \mathbb{R}\} \) Vì \({x^2} + 1 \ge 1\;\forall x \in \mathbb{R}\) nên \(T = [1; + \infty )\) Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1\) Hay \(S\left( {0;1} \right).\) Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
|