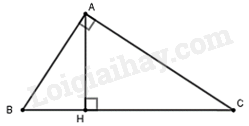
SBT Toán 9 - giải SBT Toán 9 - Kết nối tri thức với cuộc sống

Giải bài 4.20 trang 48, 49 sách bài tập toán 9 - Kết nối tri thức tập 1

Cho tam giác ABC vuông tại A, AH là đường cao. Chứng minh rằng (frac{1}{{A{H^2}}} = frac{1}{{A{B^2}}} + frac{1}{{A{C^2}}}). (HD: ta có (sin B = frac{{AH}}{{AB}},sin C = frac{{AH}}{{AC}},cos B = sin C) và áp dụng công thức ({sin ^2}alpha + {cos ^2}alpha = 1) với mọi góc nhọn (alpha )).

Tổng hợp Đề thi vào 10 có đáp án và lời giải

Toán - Văn - Anh

Đề bài

Cho tam giác ABC vuông tại A, AH là đường cao. Chứng minh rằng $\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}$ .

(HD: ta có $\sin B = \frac{{AH}}{{AB}},\sin C = \frac{{AH}}{{AC}},\cos B = \sin C$ và áp dụng công thức ${\sin ^2}\alpha + {\cos ^2}\alpha = 1$ với mọi góc nhọn $\alpha$ ).

Phương pháp giải - Xem chi tiết

+ Tam giác ABH vuông tại H nên $\sin B = \frac{{AH}}{{AB}}$ suy ra $\frac{1}{{A{B^2}}} = \frac{{{{\sin }^2}B}}{{A{H^2}}}$ .

+ Tam giác AHC vuông tại H nên $\sin C = \frac{{AH}}{{AC}}$ suy ra $\frac{1}{{A{C^2}}} = \frac{{{{\sin }^2}C}}{{A{H^2}}}$

+ Vì B và C là hai góc phụ nhau nên $\cos B = \sin C$ , suy ra ${\cos ^2}B = {\sin ^2}C$ .

+ $\frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{{{{\sin }^2}C}}{{A{H^2}}} + \frac{{{{\sin }^2}B}}{{A{H^2}}} = \frac{{{{\cos }^2}B + {{\sin }^2}B}}{{A{H^2}}} = \frac{1}{{A{H^2}}}$

Lời giải chi tiết

Tam giác ABH vuông tại H nên $\sin B = \frac{{AH}}{{AB}}$ ,

do đó, $\frac{1}{{AB}} = \frac{{\sin B}}{{AH}}$ ,

suy ra $\frac{1}{{A{B^2}}} = \frac{{{{\sin }^2}B}}{{A{H^2}}}$ .

Tam giác AHC vuông tại H nên $\sin C = \frac{{AH}}{{AC}}$ ,

do đó $\frac{1}{{AC}} = \frac{{\sin C}}{{AH}}$ ,

suy ra $\frac{1}{{A{C^2}}} = \frac{{{{\sin }^2}C}}{{A{H^2}}}$ .

Vì B và C là hai góc phụ nhau nên $\cos B = \sin C$ , suy ra ${\cos ^2}B = {\sin ^2}C$ .

Ta có:

$\frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{{{{\sin }^2}C}}{{A{H^2}}} + \frac{{{{\sin }^2}B}}{{A{H^2}}} = \frac{{{{\cos }^2}B + {{\sin }^2}B}}{{A{H^2}}} = \frac{1}{{A{H^2}}}$

Chia sẻ

Bình luận

Bình chọn:

3.9 trên 8 phiếu

Giải bài 4.21 trang 49 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho tam giác ABC có (BC = 11cm,widehat {ABC} = {38^o},widehat {ACB} = {30^o}). Gọi H là chân đường vuông góc kẻ từ A đến BC. Hãy tính AH.
Giải bài 4.22 trang 49 sách bài tập toán 9 - Kết nối tri thức tập 1
Giải tam giác ABC vuông tại A, với (AB = c,BC = a,CA = b) trong các trường hợp (cạnh làm tròn đến chữ số thập phân thứ ba): a) (a = 5,widehat B = {50^o}); b) (b = 5,widehat B = {40^o}); c) (b = 5,widehat C = {55^o}).
Giải bài 4.23 trang 49 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho A, B là hai địa điểm ở hai bên bờ sông, biết AN và PM cùng vuông góc MN, (MN = n) (mét), (MP = p) (mét), (p > n) và (widehat {MPA} = alpha ) (H.4.12). Chứng minh rằng: (AB = frac{{ptan alpha - n}}{{sin alpha }}).
Giải bài 4.24 trang 49 sách bài tập toán 9 - Kết nối tri thức tập 1
Một người đứng xa tòa nhà 100m, dùng giác kế thẳng đứng ngắm thấy điểm trên nóc nhà với góc nhìn ({15^o}) (so với phương nằm ngang) (H.4.13). Hỏi tòa nhà cao bao nhiêu mét (làm tròn đến chữ số thập phân thứ nhất), biết chiều cao của giác kế là 1,7m?
Giải bài 4.25 trang 50 sách bài tập toán 9 - Kết nối tri thức tập 1
Hai trạm quan trắc tàu biển đặt ở hai mỏm núi A và B cách nhau 2km, nhìn thấy chiếc tàu C ở phía xa với (widehat {CAB} = {50^o},widehat {CBA} = {45^o}) (H.4.14). Hỏi tàu còn cách đường thẳng AB bao nhiêu mét?

Luyện Bài Tập Trắc nghiệm Toán 9 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho Lớp 9 - Ôn Thi Vào Lớp 10 Miễn Phí

>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link

Giải bài 4.20 trang 48, 49 sách bài tập toán 9 - Kết nối tri thức tập 1

Tham Gia Group Dành Cho Lớp 9 - Ôn Thi Vào Lớp 10 Miễn Phí

Góp ý

Báo lỗi góp ý

Báo lỗi