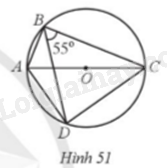
Giải bài 48 trang 123 sách bài tập toán 9 - Cánh diều tập 1Ở Hình 5, cho hai hình chóp tứ giác đều S.ABCD và S’.A’B’C’D’ có cùng chiều cao SH= S’H = 30 cm. Thể tích của hình chóp S.ABCD nhỏ hơn thể tích của hình chóp S’A’B’C’D' là 240 cm3. Tính độ dài cạnh đáy của mỗi hình chóp, biết \(A'B' - AB = 2\)cm. Đề bài Cho các điểm A, B, C, D thuộc đường tròn tâm O đường kính \(AC = 2\)cm với \(\widehat {CBD} = 55^\circ \) (Hình 51)
a) Số đo góc CAD là A. 35° B. 145° C. 55° D. 125° b) Độ dài đoạn thẳng CD là A. 2cos55° cm B. 2sin55° cm C. 2tan55° cm D. 2cot55° cm Phương pháp giải - Xem chi tiết a) Chỉ ra 2 góc nội tiếp cùng chắn 1 cung thì bằng nhau. b) Áp dụng tỉ số lượng giác trong tam giác vuông ACD. Lời giải chi tiết a) Xét (O) có: Góc DBC và DAC là 2 góc nội tiếp cùng chắn cung DC nên \(\widehat {DBC} = \widehat {DAC} = 55^\circ \) (cùng bằng nửa số đo cung DC). Đáp án C. b) Do góc ADC là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ADC} = 90^\circ \). Xét tam giác ADC vuông tại D có: \(DC = AC.\sin \widehat {DAC} = 2.\sin 55^\circ \)cm. Đáp án B.
|