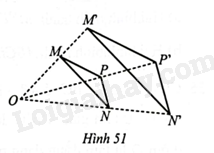
Giải bài 51 trang 81 sách bài tập toán 8 – Cánh diềuCho điểm \(O\) nằm ngoài tam giác \(MNP\). Trên các tia \(OM,ON,OP\) ta lần lượt lấy các điểm \(M',N',P'\) Đề bài Cho điểm \(O\) nằm ngoài tam giác \(MNP\). Trên các tia \(OM,ON,OP\) ta lần lượt lấy các điểm \(M',N',P'\) sao cho \(\frac{{OM'}}{{OM}} = \frac{{ON'}}{{ON}} = \frac{{OP'}}{{OP}} = \frac{5}{3}\) (Hình 51). a) Tam giác \(M'N'P'\) có đồng dạng phối cảnh với tam giác \(MNP\) hay không? Nếu có, hãy chỉ ra tâm đồng dạng phối cảnh. b) Hãy chỉ ra đoạn thẳng \(AB\) sao cho hai đoạn thẳng \(AB\) và \(MP\) đồng dạng phối cảnh, điểm \(O\) là tâm đồng dạng phối cảnh và \(\frac{{OA}}{{OM}} = \frac{{OB}}{{OP}} = \frac{1}{4}\)
Phương pháp giải - Xem chi tiết Bằng cách “phóng to” (nếu tỉ số vị tự \(k > 1\)) hay “thu nhỏ” (nếu tỉ số vị tự \(k < 1\)) hình \(H\), ta sẽ nhận được hình \(H'\) đồng dạng phối cảnh (hay vị tự) với hình \(H\). Ta gọi hình \(H'\) là hình đồng dạng phối cảnh (hay vị tự) tỉ số \(k\) của hình \(H\) Hình đồng dạng phối cảnh tỉ số k của đoạn thẳng \(AB\) là một đoạn thẳng \(A'B'\) (nằm trên đường thẳng song song hoặc trùng với đường thẳng \(AB\)) và \(A'B' = k.AB\) Hai tam giác \(A'B'C'\) và \(ABC\) gọi là đồng dạng phối cảnh (hay vị tự) với nhau, điểm \(O\) gọi là tâm đồng dạng phối cảnh, tỉ số \(k = \frac{{A'B'}}{{AB}}\) gọi là tỉ số vị tự. Lời giải chi tiết a) Tam giác \(M'N'P'\) đồng dạng phối cảnh với tam giác \(MNP\) và \(O\) là tâm đồng dạng phối cảnh. b) Gọi \(KH\) là đường trung bình của tam giác \(MOP\left( {K \in OM,H \in OP} \right)\) Lấy \(A,B\) lần lượt là trung điểm của \(OK,OH\). Khi đó, hai đoạn thẳng \(AB\) và \(MP\) đồng dạng phối cảnh, điểm \(O\) là tâm đồng dạng phối cảnh và \(\frac{{OA}}{{OM}} = \frac{{OB}}{{OP}} = \frac{1}{4}\)
|