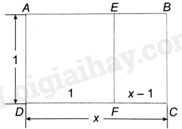
Giải bài 6.26 trang 17 sách bài tập toán 9 - Kết nối tri thức tập 2Hình chữ nhật vàng là hình chữ nhật có thể chia thành một hình vuông và hình chữ nhật thứ hai có các kích thước tỉ lệ với các kích thước tương ứng của hình chữ nhật ban đầu (với cùng hệ số tỉ lệ). Tỉ số x giữa chiều dài và chiều rộng của hình chữ nhật vàng được gọi là tỉ lệ vàng. a) Tính tỉ số giữa chiều dài và chiều rộng của hình chữ nhật ABCD và hình chữ nhật EBCF. b) Tìm giá trị chính xác của tỉ lệ vàng bằng cách đặt hai tỉ số ở câu a bằng nhau rồi tìm x. Đề bài Hình chữ nhật vàng là hình chữ nhật có thể chia thành một hình vuông và hình chữ nhật thứ hai có các kích thước tỉ lệ với các kích thước tương ứng của hình chữ nhật ban đầu (với cùng hệ số tỉ lệ). Tỉ số x giữa chiều dài và chiều rộng của hình chữ nhật vàng được gọi là tỉ lệ vàng.
a) Tính tỉ số giữa chiều dài và chiều rộng của hình chữ nhật ABCD và hình chữ nhật EBCF. b) Tìm giá trị chính xác của tỉ lệ vàng bằng cách đặt hai tỉ số ở câu a bằng nhau rồi tìm x. Phương pháp giải - Xem chi tiết a) Giả sử hình chữ nhật ABCD có chiều rộng \(AD = BC = 1cm\) và chiều dài \(AB = CD = x\left( {cm} \right)\). Điều kiện \(x > 1\) nên tính được tỉ số giữa chiều dài và chiều rộng của hình chữ nhật ABCD. + Chiều dài của hình chữ nhật EBCF là \(AD = EF = 1cm\) và chiều rộng là \(EB = FC = x - 1\left( {cm} \right)\), từ đó tính được tỉ số giữa chiều dài và chiều rộng của hình chữ nhật EBCF. b) + Theo đề bài ta có phương trình: \(\frac{x}{1} = \frac{1}{{x - 1}}\). + Giải phương trình thu được, kết hợp với điều kiện và đưa ra kết luận. Lời giải chi tiết a) Giả sử hình chữ nhật ABCD có chiều rộng \(AD = BC = 1cm\) và chiều dài \(AB = CD = x\left( {cm} \right)\). Điều kiện \(x > 1\). Do đó tỉ số giữa chiều dài và chiều rộng của hình chữ nhật ABCD là \(\frac{x}{1}\). Từ hình vẽ ta thấy chiều dài của hình chữ nhật EBCF là \(AD = EF = 1cm\) và chiều rộng là \(EB = FC = x - 1\left( {cm} \right)\). Do đó, tỉ số chiều dài và chiều rộng của hình chữ nhật EBCF là: \(\frac{1}{{x - 1}}\). b) Theo đề bài ta có phương trình: \(\frac{x}{1} = \frac{1}{{x - 1}}\) Nhân hai vế của phương trình này với \(x - 1\) để khử mẫu ta được \(x\left( {x - 1} \right) = 1\) hay \({x^2} - x - 1 = 0\). Ta có: \(\Delta = {\left( { - 1} \right)^2} - 4.1.\left( { - 1} \right) = 5\) nên phương trình có hai nghiệm \({x_1} = \frac{{1 + \sqrt 5 }}{2}\) (thỏa mãn) và \({x_2} = \frac{{1 - \sqrt 5 }}{2}\) (không thỏa mãn). Vậy tỉ lệ vàng là \(\frac{{1 + \sqrt 5 }}{2}\).
|