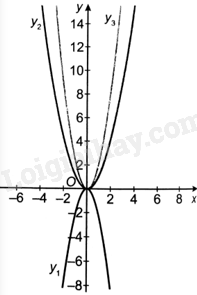
Giải bài 6.5 trang 6 sách bài tập toán 9 - Kết nối tri thức tập 2Trong hình bên có đồ thị của ba hàm số (y = - 2{x^2},y = {x^2},y = 2{x^2}). a) Cho biết đường nào là đồ thị của hàm số (y = - 2{x^2}). b) Trong hai đường còn lại, với mỗi x hãy so sánh hai giá trị tương ứng của y để phân biệt đồ thị của hai hàm số (y = {x^2}) và (y = 2{x^2}). Đề bài Trong hình bên có đồ thị của ba hàm số \(y = - 2{x^2},y = {x^2},y = 2{x^2}\).
a) Cho biết đường nào là đồ thị của hàm số \(y = - 2{x^2}\). b) Trong hai đường còn lại, với mỗi x hãy so sánh hai giá trị tương ứng của y để phân biệt đồ thị của hai hàm số \(y = {x^2}\) và \(y = 2{x^2}\). Phương pháp giải - Xem chi tiết Đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) là một đường cong có tính chất: Nằm phía trên trục hoành nếu \(a > 0\) và nằm phía dưới trục hoành nếu \(a < 0\). Lời giải chi tiết a) Đường cong nằm phía dưới trục hoành Ox là đồ thị của hàm số \(y = - 2{x^2}\) nên đường \({y_1}\) là đồ thị của hàm số \(y = - 2{x^2}\). b) Thay \(x = 2\) vào hàm số \(y = {x^2}\) ta có: \(y = {2^2} = 4\) nên điểm (2; 4) thuộc đồ thị hàm số \(y = {x^2}\). Do đó, đồ thị của hàm số \(y = {x^2}\) là đường thẳng \({y_2}\). Thay \(x = 2\) vào hàm số \(y = 2{x^2}\) ta có: \(y = {2.2^2} = 8\) nên điểm (2; 8) thuộc đồ thị hàm số \(y = 2{x^2}\). Do đó, đồ thị của hàm số \(y = 2{x^2}\) là đường thẳng \({y_3}\).
|