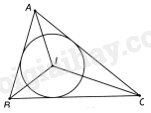
Giải bài 9.16 trang 53 sách bài tập toán 9 - Kết nối tri thức tập 2Cho tam giác ABC ngoại tiếp đường tròn (I). Chứng minh rằng: (widehat {BIC} = {90^o} + frac{{widehat {BAC}}}{2};widehat {CIA} = {90^o} + frac{{widehat {CBA}}}{2};widehat {AIB} = {90^o} + frac{{widehat {ACB}}}{2}). Đề bài Cho tam giác ABC ngoại tiếp đường tròn (I). Chứng minh rằng: \(\widehat {BIC} = {90^o} + \frac{{\widehat {BAC}}}{2};\widehat {CIA} = {90^o} + \frac{{\widehat {CBA}}}{2};\widehat {AIB} = {90^o} + \frac{{\widehat {ACB}}}{2}\). Phương pháp giải - Xem chi tiết + Chứng minh \(\widehat {ABC} + \widehat {ACB} = {180^o} - \widehat {BAC}\), \(\widehat {IBC} = \frac{{\widehat {ABC}}}{2};\widehat {ICB} = \frac{{\widehat {ACB}}}{2}\) nên \(\widehat {IBC} + \widehat {ICB} = {90^o} - \frac{{\widehat {BAC}}}{2}\). + Do đó, \(\widehat {BIC} = {180^o} - \widehat {IBC} - \widehat {ICB} = {90^o} + \frac{{\widehat {BAC}}}{2}\). + Chứng minh tương tự ta có: \(\widehat {CIA} = {90^o} + \frac{{\widehat {CBA}}}{2};\widehat {AIB} = {90^o} + \frac{{\widehat {ACB}}}{2}\). Lời giải chi tiết
Vì I là giao điểm của các đường phân giác của tam giác ABC nên \(\widehat {IBC} = \frac{{\widehat {ABC}}}{2};\widehat {ICB} = \frac{{\widehat {ACB}}}{2}\). Tam giác ABC có: \(\widehat {ABC} + \widehat {ACB} + \widehat {BAC} = {180^o}\) nên \(\widehat {ABC} + \widehat {ACB} = {180^o} - \widehat {BAC}\). Do đó, \(\widehat {IBC} + \widehat {ICB} = \frac{{\widehat {ABC} + \widehat {ACB}}}{2} = {90^o} - \frac{{\widehat {BAC}}}{2}\). Tam giác BIC có: \(\widehat {BIC} = {180^o} - \widehat {IBC} - \widehat {ICB} \\= {180^o} - {90^o} + \frac{{\widehat {BAC}}}{2} = {90^o} + \frac{{\widehat {BAC}}}{2}.\) Chứng minh tương tự ta có: \(\widehat {CIA} = {90^o} + \frac{{\widehat {CBA}}}{2};\) \(\widehat {AIB} = {90^o} + \frac{{\widehat {ACB}}}{2}\).
|