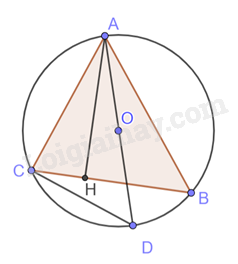
Giải bài tập 12 trang 104 SGK Toán 9 tập 1 - Chân trời sáng tạoCho tam giác ABC có ba đỉnh nằm trên đường tròn (O) và AH là đường cao. Đường thẳng AO cắt đường tròn (O) tại điểm thứ hai D. Chứng minh rằng a) AC vuông góc với DC b) (widehat {ABC} = widehat {ADC}) c) AB. AC = AH. AD Đề bài Cho tam giác ABC có ba đỉnh nằm trên đường tròn (O) và AH là đường cao. Đường thẳng AO cắt đường tròn (O) tại điểm thứ hai D. Chứng minh rằng a) AC vuông góc với DC b) \(\widehat {ABC} = \widehat {ADC}\) c) AB. AC = AH. AD Video hướng dẫn giải Phương pháp giải - Xem chi tiết Đọc kĩ dữ liệu để vẽ hình. a) Dựa vào: Góc nội tiếp chắn nửa đường tròn là góc vuông b) Dựa vào: Hai góc nội tiếp cùng chắn một cung thì bằng nhau. c) Chứng minh \(\Delta \)ABH \(\backsim \)\(\Delta \)ADC (g.g) Lời giải chi tiết
a) Ta có \(\widehat {ACD}\) chắn đường kính AD nên \(\widehat {ACD} = {90^o}\). Do đó \(AC \bot CD\) b) Ta có \(\widehat {ABC};\widehat {ADC}\) là góc nội tiếp cùng chắn cung AC nên \(\widehat {ABC} = \widehat {ADC}\). c) Tam giác ACD có 3 đỉnh nằm trên đường tròn và AD là đường kính nên tam giác ACD vuông tại C. Suy ra \(\widehat {AHB} = \widehat {ACD}\) \(\widehat {ABC} = \widehat {ADC}\) (hai góc nội tiếp cùng chắn cung AC) Vậy \(\Delta \)ABH \(\backsim \)\(\Delta \)ADC (g.g) Do đó, \(\frac{{AB}}{{AD}} = \frac{{AH}}{{AC}}\) hay AB.AC = AD.AH (đpcm)
|