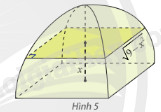
Giải bài tập 24 trang 30 SGK Toán 12 tập 2 - Chân trời sáng tạoMột chiếc lều mái vòm có hình dạng như hình dưới đây. Nếu cắt lều bằng mặt phẳng song song với mặt đáy và cách mặt đáy một khoảng (x{rm{ }}left( {rm{m}} right)) (left( {0 le x le 3} right)) thì được hình vuông có cạnh (sqrt {9 - {x^2}} {rm{ }}left( {rm{m}} right)). Tính thể tích của lều. Đề bài Một chiếc lều mái vòm có hình dạng như hình 5. Nếu cắt lều bằng mặt phẳng song song với mặt đáy và cách mặt đáy một khoảng \(x{\rm{ }}\left( {\rm{m}} \right)\) \(\left( {0 \le x \le 3} \right)\) thì được hình vuông có cạnh \(\sqrt {9 - {x^2}} {\rm{ }}\left( {\rm{m}} \right)\). Tính thể tích của lều. Phương pháp giải - Xem chi tiết Chọn trục \(Ox\) sao cho \(O\) trùng với tâm của đáy, chiều dương của trục là chiều hướng lên trên. Nếu cắt lều bởi một mặt phẳng cách mặt đáy \(x{\rm{ }}\left( {\rm{m}} \right)\), thì mặt phẳng đó cắt trục \(Ox\) tại điểm có hoành độ \(x\). Diện tích mặt cắt là \(S\left( x \right)\). Thể tích của lều là \(V = \int\limits_0^3 {S\left( x \right)dx} \). Lời giải chi tiết Chọn trục \(Ox\) sao cho \(O\) trùng với tâm của đáy, chiều dương của trục là chiều hướng lên trên. Nếu cắt lều bởi một mặt phẳng cách mặt đáy \(x{\rm{ }}\left( {\rm{m}} \right)\), thì mặt phẳng đó cắt trục \(Ox\) tại điểm có hoành độ \(x\). Mặt cắt là hình vuông có cạnh \(\sqrt {9 - {x^2}} {\rm{ }}\left( {\rm{m}} \right)\). Như vậy, diện tích mặt cắt là: \(S\left( x \right) = {\left( {\sqrt {9 - {x^2}} } \right)^2} = 9 - {x^2}\). Suy ra thể tích của lều là: \(V = \int\limits_0^3 {S\left( x \right)dx} = \int\limits_0^3 {\left( {9 - {x^2}} \right)dx} \) \(= \left. {\left( {9x - \frac{{{x^3}}}{3}} \right)} \right|_0^3 = 18\) (\({{\rm{m}}^3}\)).
|