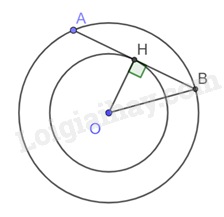
Giải bài tập 5 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo

Đề bài

Cho hai đường tròn đồng tâm (O; R) và (O; $\frac{{R\sqrt 3 }}{2}$). Một tiếp tuyến của đường tròn nhỏ cắt đường tròn lớn tại hai điểm A và B. Tính số đo cung AB.

Lời giải chi tiết

Gọi H là tiếp điểm của tiếp tuyến của đường tròn đã cho.

Xét tam giác OHB vuông tại H, ta có:

cos$\widehat {HOB}$= $\frac{{OH}}{{OB}} = \frac{{\frac{{R\sqrt 3 }}{2}}}{R} = \frac{{\sqrt 3 }}{2}$

suy ra $\widehat {HOB}$ = 30^o

Ta có OA = OB (= R) nên tam giác OAB cân tại O

Mà OH là đường cao của tam giác AOB

Nên OH cũng là đường phân giác của tam giác AOB

Suy ra $\widehat {AOB} = 2\widehat {HOB} = {2.30^o} = {60^o}$

Do đó sđ$\overset\frown{AB}$ =$\widehat {AOB} = {60^o}$.