Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạoTrong không gian Oxyz, làm thế nào để xác định một mặt phẳng bằng phương pháp tọa độ? Đề bài Trong không gian Oxyz, làm thế nào để xác định một mặt phẳng bằng phương pháp tọa độ?
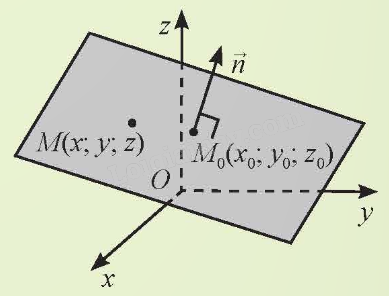
Phương pháp giải - Xem chi tiết Sử dụng kiến thức đã học. Lời giải chi tiết Trong không gian Oxyz, để xác định một mặt phẳng ta cần biết được 1 điểm mà đường thẳng đó đi và một vectơ pháp tuyến của mặt phẳng đó.
|