Giải câu hỏi trang 68, 69, 70 SGK Toán 9 tập 2 - Kết nối tri thứcVẽ đường tròn tâm O có bán kính bằng 2cm và dây cung AB có độ dài bằng 2cm. Lấy một điểm C tùy ý nằm trên cung lớn AmB (H.9.2). a) Cho biết số đo góc ở tâm AOB và số đo của cung bị chắn AB. b) Đo góc ACB và so sánh với kết quả của bạn bên cạnh. c) Lấy điểm D tùy ý nằm trên cung ACB. Đo góc ADB và so sánh với các góc ACB và AOB.
Lựa chọn câu để xem lời giải nhanh hơn
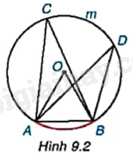
HĐ Video hướng dẫn giải Trả lời câu hỏi Hoạt động trang 68 SGK Toán 9 Kết nối tri thức Vẽ đường tròn tâm O có bán kính bằng 2cm và dây cung AB có độ dài bằng 2cm. Lấy một điểm C tùy ý nằm trên cung lớn AmB (H.9.2).
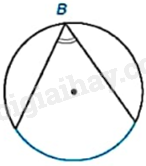
a) Cho biết số đo góc ở tâm AOB và số đo của cung bị chắn AB. b) Đo góc ACB và so sánh với kết quả của bạn bên cạnh. c) Lấy điểm D tùy ý nằm trên cung ACB. Đo góc ADB và so sánh với các góc ACB và AOB. Phương pháp giải: a) Chứng minh tam giác AOB đều, suy ra \(\widehat {AOB} = {60^o}\). Do đó, \(sđ\overset\frown{AB}=\widehat{AOB}={{60}^{o}}\) (góc ở tâm chắn cung AB). b, c) Sử dụng thước đo góc đo được góc ACB, góc ADB đều bằng 30 độ. Do đó, \(\widehat {ACB} = \widehat {ADB}\) Lời giải chi tiết: Vì A, B thuộc đường tròn tâm O nên \(OA = OB = 2cm\). Tam giác AOB có: \(OA = OB = AB = 2cm\) nên tam giác ABO đều. Do đó, \(\widehat {AOB} = {60^o}\). Suy ra: \(sđ\overset\frown{AB}=\widehat{AOB}={{60}^{o}}\) (góc ở tâm chắn cung AB). b) Sử dụng thước đo góc, ta đo được \(\widehat {ACB} = {30^o}\). c) Sử dụng thước đo góc, ta đo được \(\widehat {ADB} = {30^o}\). Do đó, \(\widehat {ADB} = \widehat {ACB}\) và \(\widehat {ADB} = \frac{1}{2}\widehat {AOB}\). CH Video hướng dẫn giải Trả lời câu hỏi Câu hỏi trang 70 SGK Toán 9 Kết nối tri thức Hãy cho biết số đo góc nội tiếp tìm được trong Hình 9.3 ở Ví dụ 1, biết rằng số đo của các cung màu xanh trong hình đều bằng \({120^o}\). Phương pháp giải: Vì B là góc nội tiếp trong đường tròn nên có số đo bằng nửa số đo cung bị chắn, từ đó tính được góc B. Lời giải chi tiết:
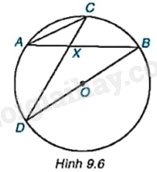
Vì B là góc nội tiếp trong đường tròn nên \(\widehat B = \frac{1}{2}{.120^o} = {60^o}\). LT Video hướng dẫn giải Trả lời câu hỏi Luyện tập trang 70 SGK Toán 9 Kết nối tri thức Cho đường tròn tâm O và hai dây cung AB, CD cắt nhau tại điểm X nằm trong đường tròn (H.9.6). Chứng minh rằng $\Delta AXC\backsim \Delta DXB$.
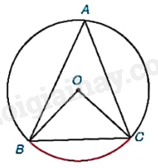
Phương pháp giải: + Sử dụng định lí về mối quan hệ giữa góc nội tiếp và cung bị chắn để chứng minh \(\widehat {ACX} = \widehat {XBD}\). + Chứng minh $\Delta AXC\backsim \Delta DXB$ theo trường hợp góc – góc. Lời giải chi tiết: Vì góc ACX và góc XBD là góc nội tiếp cùng chắn cung AD của đường tròn tâm O nên: \(\widehat {ACX} = \widehat {XBD}\). Tam giác AXC và tam giác DXB có: \(\widehat {ACX} = \widehat {XBD}\) (cmt), \(\widehat {AXC} = \widehat {BXD}\) (hai góc đối đỉnh). Do đó, $\Delta AXC\backsim \Delta DXB$ (g – g). VD Video hướng dẫn giải Trả lời câu hỏi Vận dụng trang 70 SGK Toán 9 Kết nối tri thức Trở lại tình huống mở đầu, hãy tính số đo của góc BAC nếu đường tròn có bán kính 2cm và dây cung \(BC = 2\sqrt 2 cm\). Chúng ta đã biết số đo góc ở tâm BOC của đường tròn (O) trong Hình 9.1 bằng số đo của cung bị chắn.
Phương pháp giải: + Theo định lí Pythagore đảo chứng minh được tam giác BOC vuông tại O, tính được góc BOC. + Vì góc BOC và góc BAC lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung BC của đường tròn (O) nên \(\widehat {BAC} = \frac{1}{2}\widehat {BOC}\). Lời giải chi tiết: Vì B, C thuộc đường tròn (O) nên \(OB = OC = 2cm\). Xét tam giác BOC có: \(O{B^2} + O{C^2} = B{C^2}\left( {do\;{2^2} + {2^2} = {{\left( {2\sqrt 2 } \right)}^2}} \right)\) nên tam giác BOC vuông tại O (định lí Pythagore đảo). Suy ra, \(\widehat {BOC} = {90^o}\) Vì góc BOC và góc BAC lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung BC của đường tròn (O) nên \(\widehat {BAC} = \frac{1}{2}\widehat {BOC} = \frac{1}{2}{.90^o} = {45^o}\).
|