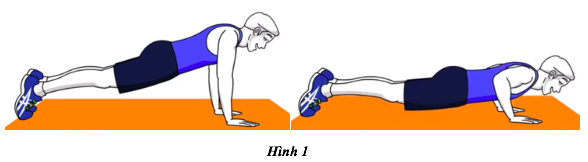
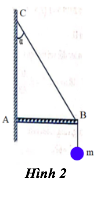
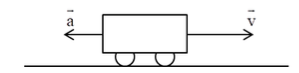
Giải đề thi học kì 1 lý lớp 10 năm 2019 - 2020 trường THPT Nguyễn Hữu HuânGiải chi tiết đề thi học kì 1 môn lý lớp 10 năm 2019 - 2020 trường THPT Nguyễn Hữu Huân với cách giải nhanh và chú ý quan trọng Câu 1. (2,0 điểm) - Chuyển động thẳng biến đổi đều là gì? (1,0 điểm) - Một chiếc xe đang chuyển động thẳng chận dần đều trên đường nằm ngang, em hãy vẽ vectơ vận tốc \(\overrightarrow v \) và vectơ gia tốc \(\overrightarrow a \) của xe. (1,0 điểm) Câu 2. (2,0 điểm) - Hãy nêu điểm khác nhau giữa cặp (hai) lực trực đối cân bằng và cặp (hai) lực trực đối không cân bằng. (1,0 điểm) - Chống đẩy hay hít đất là một bài tập thể dục thông thường được thực hiện bằng cách nâng cao và hạ thấp cơ thể trong tư thế nằm sấp bằng cách sử dụng cánh tay (hình 1). Xét 3 lực: (1) Trọng lực tác dụng lên người, (2) Áp lực của người tác dụng lên sàn và (3) Phản lực do sàn tác dụng lên người. Em hãy chỉ ra cặp lực trực đối cân bằng và cặp lực trực đối không cân bằng. (1,0 điểm) Câu 3. (2,0 điểm) a) Phát biểu và viết biểu thức của định luật Húc (Hooke) (1,0 điểm) b) Treo một vật có trọng lượng 4 N vào đầu dưới của một lò xo treo thẳng đứng, đầu trên của lò xo gắn cố định thì lò xo dãn ra 20 mm. + Vẽ hình, phân tích lực tác dụng vào vật. (0,25 điểm) + Tính độ cứng k của lò xo. (0,75 điểm) Câu 4. (2,0 điểm) Trong một trận đấu bóng chuyền, một vận động viên nhảy lên cao để đập giao bóng từ độ cao h = 3 m đối với mặt đất và đập bóng theo phương ngang, vuông góc với lưới với vận tốc v0 = 20 m/s. Lấy g = 10 m/s2. Bỏ qua lực cản của không khí. a) Trong trường hợp bóng bay qua lưới, tìm thời gian chuyển động của bóng trong không khí và tầm xa của bóng. (1 điểm) b) Viết phương trình quỹ đạo của bóng. (0,5 điểm) c) Biết rằng mép trên của lưới cao 2,24 m đối với mặt đất và bóng vừa qua sát mép trên của lưới. Hỏi vận động viên đứng cách lưới theo phương ngang một khoảng bao nhiêu? (0,5 điểm) Câu 5. (2 điểm) Một ngọn đèn khối lượng m = 4 kg được treo vào tường bởi dây BC và thanh AB (hình 2). Thanh AB gắn vào tường bằng bản lề A, \(\alpha = {30^0}\). Khối lượng của thanh AB là 2 kg. Tìm lực căng dây và phản lực do bản lề tác dụng lên thanh AB. Lấy g = 10 m/s2.
HƯỚNG DẪN GIẢI CHI TIẾT Thực hiện: Ban chuyên môn HocTot.XYZ Câu 1. Phương pháp: Sử dụng lý thuyết về chuyển động thẳng biến đổi đều. Chuyển động thẳng chậm dần đều có vectơ vận tốc ngược chiều với vectơ gia tốc. Cách giải: - Chuyển động thẳng biến đổi đều là là chuyển động thẳng trong đó gia tốc tức thời không đổi. - Chuyển động thẳng chậm dần đều có vectơ vận tốc ngược chiều với vectơ gia tốc. Hình vẽ biểu diễn vectơ vận tốc \(\overrightarrow v \) và vectơ gia tốc \(\overrightarrow a \) của một chiếc xe đang chuyển động chậm dần đều: Câu 2. Phương pháp: Sử dụng lí thuyết về cặp (hai) lực trực đối: hai lực tác dụng vào hai vật khác nhau, có cùng phương, cùng độ lớn nhưng ngược chiều nhau. Cách giải: - Điểm khác nhau giữa cặp (hai) lực trực đối cân bằng và cặp (hai) lực trực đối không cân bằng là: + Cặp (hai) lực trực đối cân bằng là cặp (hai) lực tác dụng vào hai vật khác nhau, có cùng phương, cùng độ lớn nhưng ngược chiều nhau. + Cặp (hai) lực trực đối không cân bằng là cặp (hai) lực tác dụng vào hai vật khác nhau, có cùng độ lớn và cùng chiều. - Phân tích các lực: (1) Trọng lực tác dụng lên người: có điểm đặt ở người, phương thẳng đứng, chiều hướng xuống. (2) Áp lực của người tác dụng lên sàn: có điểm đặt ở sàn, phương thẳng đứng, chiều hướng xuống. (3) Phản lực do sàn tác dụng lên người: có điểm đặt ở người, phương thẳng đứng, chiều hướng lên. Vậy cặp lực trực đối cân bằng là: (2) – (3) Cặp lực trực đối không cân bằng là: (1) – (2) Câu 3. Phương pháp: Định luật Húc: Trong giới hạn đàn hồi, lực đàn hồi của lò xo tỉ lệ thuận với độ biến dạng của lò xo. Công thức định luật Húc: \({{\rm{F}}_{dh}}{\rm{ = }} - {\rm{k}}\Delta {\rm{l}}\) Cách giải:
a) Phát biểu định luật Húc: Trong giới hạn đàn hồi, lực đàn hồi của lò xo tỉ lệ thuận với độ biến dạng của lò xo. Biểu thức định luật Húc: \({{\rm{F}}_{dh}}{\rm{ = }} - {\rm{k}}\Delta {\rm{l}}\) b) Trọng lực tác dụng vào vật là: \(P = mg\) Lực đàn hồi tác dụng vào lò xo là: \({F_{dh}} = - k.\Delta {\rm{l}}\) Vì vật cân bằng nên: \(P + {F_{dh}} = 0 \Rightarrow P - k\Delta l = 0 \\\Rightarrow k = \dfrac{P}{{\Delta l}} = \dfrac{4}{{0,02}} = 200\,\,\left( {N/m} \right)\) Câu 4. Phương pháp: Chuyển động của bóng là chuyển động của vật bị ném ngang từ độ cao h. Thời gian chuyển động của bóng: \(t = \sqrt {\dfrac{{2h}}{g}} \) Tầm xa của bóng: \(L = {v_0}t = {v_0}\sqrt {\dfrac{{2h}}{g}} \) Phương trình quỹ đạo của bóng: \(y = \dfrac{g}{{2{v_0}^2}}{x^2}\) Cách giải: a) Thời gian chuyển động của bóng là: \(t = \sqrt {\dfrac{{2h}}{g}} = \sqrt {\dfrac{{2.3}}{{10}}} = 0,77\,\,\left( s \right)\) Tầm xa của bóng là: \(L = {v_0}t = {v_0}\sqrt {\dfrac{{2h}}{g}} \\= 20.\sqrt {\dfrac{{2.3}}{{10}}} = 15,49\,\,\left( m \right)\) b) Phương trình quỹ đạo của bóng là: \(y = \dfrac{g}{{2{v_0}^2}}{x^2} = \dfrac{{10}}{{{{2.20}^2}}}{x^2} = \dfrac{1}{{80}}{x^2}\) c) Thay y = 2,24 m vào phương trình quỹ đạo, ta có: \(2,24 = \dfrac{1}{{80}}{x^2} \Rightarrow x = 13,39\,\,\left( m \right)\) Vậy vận động viên đứng cách lưới theo phương ngang một khoảng 13,39 m. Câu 5. Phương pháp: Điều kiện cân bằng của vật rắn: \(\left\{ \begin{array}{l}\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + ... = \overrightarrow 0 \\{M_1} + {M_2} + ... = 0\end{array} \right.\) Sử dụng phương pháp chiếu để tính giá trị các lực. Cách giải: Ta có hình vẽ phân tích các lực tác dụng lên thanh AB. Chọn hệ trục tọa độ Oxy. Độ lớn lực \(T = P = mg = 4.10 = 40\,\,\left( N \right)\) \(P' = m'g = 2.10 = 20\,\,\left( N \right)\) Để thanh AB nằm cân bằng, ta có: \(\begin{array}{l}{M_T} + {M_{P'}} + {M_{T'}} = 0 \\\Rightarrow T.AB + P'.\dfrac{{AB}}{2} - T'.AB.cos\alpha = 0\\ \Rightarrow T' = \dfrac{{T + P'.\dfrac{1}{2}}}{{\cos \alpha }} = \dfrac{{40 + 20.\dfrac{1}{2}}}{{\cos {{30}^0}}} \\\approx 57,7\,\,\left( N \right)\end{array}\) Hợp lực tác dụng lên thanh là: \(\overrightarrow T + \overrightarrow {T'} + \overrightarrow {P'} + \overrightarrow Q = \overrightarrow 0 \) (1) Chiếu (1) lên trục Ox, ta có: \( - T'.\sin \alpha + {Q_x} = 0 \\\Rightarrow {Q_x} = T'.\sin \alpha = 57,7.sin{30^0} \\= 28,87\,\,\left( N \right)\) Chiếu (1) lên trục Oy, ta có: \(\begin{array}{l} - T + T'.cos\alpha - P' + {Q_y} = 0 \\\Rightarrow {Q_y} = T + P' - T'.cos\alpha \\ \Rightarrow {Q_y} = 40 + 20 - 57,7.cos{30^0} \\= 10\,\,\left( N \right)\end{array}\) Phản lực do bản lề tác dụng lên thanh AB là: \(Q = \sqrt {{Q_x}^2 + {Q_y}^2} \\= \sqrt {28,{{87}^2} + {{10}^2}} = 30,55\,\,\left( N \right)\) HocTot.XYZ
|