Đề thi học kì 1 môn toán lớp 10 năm 2019 - 2020 sở GDĐT Hà NamGiải chi tiết đề thi học kì 1 môn toán lớp 10 năm 2019 - 2020 sở GDĐT Hà Nam với cách giải nhanh và chú ý quan trọng Câu 1: Trong các phương trình dưới đây, phương trình nào tương đương với phương trình \({x^2} = 4?\) A. \(\left| x \right| = 2\) B. \({x^2} - 2x + 4 = 0\) C. \({x^2} + \sqrt x = \sqrt x + 4\) D. \({x^2} - 2x - 4 = 0\) Câu 2: Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD với A(2;– 2), B(3; 4), C(– 1; 5). Khi đó điểm D có tọa độ là: A. (0; 11) B. (0;–1) C. (–2; –1) D. (5; 6) Câu 3: Tìm tập nghiệm của phương trình \({x^4} - 5{x^2} - 6 = 0.\) A. \(\left\{ { - 1;\,\,6} \right\}\) B. \(\left\{ { - \sqrt 6 ;\,\,\sqrt 6 } \right\}\) C. \(\left\{ { - 1;\, - \sqrt 6 ;\,\,1;\,\,\sqrt 6 } \right\}\) D. \(\left\{ {1;\,\,\sqrt 6 } \right\}\) Câu 4: Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {x + 4} - 1}}{{x - 1}}\,\,\,khi\,\,\,x > 4\\3 - x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,\,\,x \le 4\end{array} \right..\) Tính f (5) + f (–5). A. \( - \dfrac{3}{2}\) B. \(\dfrac{{15}}{2}\) C. \(\dfrac{{17}}{2}\) D. \( - \dfrac{5}{2}\) Câu 5: Có tất cả bao nhiêu số nguyên m để phương trình \(4\sqrt {x - 2} + {m^2}\sqrt {x + 2} = 5\sqrt[4]{{{x^2} - 4}}\) có nghiệm. A. 2 B. 3 C. 1 D. 4 Câu 6: Cho hình vuông ABCD có cạnh bằng a. Tích \(\overrightarrow {AB} .\overrightarrow {AC} \) bằng: A. \(2{a^2}\) B. \({a^2}\) C. \({a^2}\sqrt 2 \) D. 0 Câu 7: Cho \(\overrightarrow u \)= (1;-2) và \(\overrightarrow v \) = (-2;2). Khi đó \(2\overrightarrow u + \overrightarrow v \) bằng: A. (-2;1) B. (-1;3) C. (0;-2) D. (2;4) Câu 8: Trong măt phẳng với hệ trục tọa độ \(\left( {O;\overrightarrow i ;\overrightarrow j } \right)\) cho các vectơ \(\overrightarrow u = 2\overrightarrow i - 3\overrightarrow j \) và \(\overrightarrow v = k\overrightarrow i + \dfrac{1}{3}\overrightarrow j \). Biết \(\overrightarrow u \bot \overrightarrow v \), khi đó k bằng: A. -4 B. 4 C. \(\dfrac{1}{2}\) D. \( - \dfrac{1}{2}\) Câu 9: Cho tam giác ABC, lấy điểm M trên cạnh BC sao cho BM = 3MC. Biểu diễn \(\overrightarrow {AM} \) theo 2 vectơ \(\overrightarrow {AB} ,\,\,\overrightarrow {AC} \) ta được: A. \(\overrightarrow {AM} = \dfrac{3}{4}\overrightarrow {AB} + \dfrac{1}{4}\overrightarrow {AC} \) B. \(\overrightarrow {AM} = \dfrac{1}{4}\overrightarrow {AB} + \dfrac{3}{4}\overrightarrow {AC} \) C. \(\overrightarrow {AM} = \dfrac{4}{3}\overrightarrow {AB} + \dfrac{1}{3}\overrightarrow {AC} \) D. \(\overrightarrow {AM} = \dfrac{1}{3}\overrightarrow {AB} + \dfrac{4}{3}\overrightarrow {AC} \) Câu 10: Tìm điều kiện của tham số m để phương trình \(\left( {5{m^2} - 4} \right)x = 2m + x\) có nghiệm. A. \(m = \pm 1\) B. \(m = \pm \dfrac{{\sqrt 5 }}{2}\) C. \(m \ne \pm \dfrac{{\sqrt 5 }}{2}\) D. \(m \ne \pm 1\) Câu 11: Cho parabol \(\left( P \right):\,\,y = a{x^2} + bx + c\) có a < 0 và tọa độ đỉnh là (2;5). Tìm điều kiện của tham số m để phương trình \(a{x^2} + bx + c = m\) vô nghiệm. A. m > 5 B. 2 < m < 5 C. m < 2 D. \(m \in \left\{ {2;5} \right\}\) Câu 12: Cho tam giác đều ABC có cạnh bằng a. Khi đó \(\left| {\overrightarrow {AB} + \overrightarrow {CA} } \right|\) bằng: A. a B. \(a\sqrt 3 \) C. 2a D. \(\dfrac{{a\sqrt 3 }}{2}\) Câu 13: Gọi A, B là các giao điểm của đồ thị hàm số \(f\left( x \right) = 3{x^2} - 2\) và \(g\left( x \right) = 2{x^2} - x + 4\). Phương trình đường thẳng AB là: A. y = –4x + 9 B. y = 3x – 12 C. y = –3x + 16 D. y = 4x – 11 Câu 14: Tìm số phần tử của tập hợp \(A = \left\{ {x \in \mathbb{Z}; - 3 < x \le 4} \right\}\). A. 6 B. 7 C. 8 D. 5 Câu 15: Tìm giao điểm của parabol \(\left( P \right):\,\,y = - {x^2} - 2x + 5\) với trục Oy. A. (0;5) B. (5;0) C. (1;4) D. (0;-5) Câu 16: Cho tam giác ABC có AM là đường trung tuyến. Gọi I là trung điểm của AM. Trong các mệnh đề sau, mệnh đề nào đúng. A. \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \) B. \(\overrightarrow {IA} + 2\overrightarrow {IB} + 2\overrightarrow {IC} = \overrightarrow 0 \) C. \(2\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \) D. \(2\overrightarrow {IA} - \overrightarrow {IB} - \overrightarrow {IC} = \overrightarrow 0 \) Câu 17: Cho tập hợp A gồm 3 phần tử. Hỏi tập hợp A có bao nhiêu tập con. A. 4 B. 8 C. 6 D. 3 Câu 18: Cho hàm số \(y = \left( {m - 5} \right){x^2} - 5x + 1\). Hàm số đã cho là hàm số bậc nhất khi: A. m = 5 B. m > 5 C. m < 5 D. \(m \ne 5\) Câu 19: Hàm số nào dưới đây là hàm số chẵn trên tập xác định của nó? A. \(y = \dfrac{4}{x}\) B. \(y = 4{x^3} - 2x\) C. \(y = \sqrt {x + 1} \) D. \(y = - {x^4} + 3{x^2} + 1\) Câu 20: Gọi S là tập hợp tất cả các giá trị của tham số m để đồ thị hàm số \(y = {x^2} + 5x + 2m\) cắt trục Ox tại hai điểm phân biệt A, B thỏa mãn OA = 4OB. Tổng các phần tử của S bằng: A. \(\dfrac{{43}}{9}\) B. \(\dfrac{{68}}{9}\) C. \( - \dfrac{{41}}{9}\) D. \( - \dfrac{{32}}{9}\) Câu 21: Xác định hàm số bậc hai \(y = a{x^2} - x + c\) biết đồ thị hàm số đi qua A(1;-2) và B(2;3). A. \(y = 3{x^2} - x - 4\) B. \(y = {x^2} - 3x + 5\) C. \(y = 2{x^2} - x - 3\) D. \(y = - {x^2} - 4x + 3\) Câu 22: Hàm số \(y = - {x^2} + 5x - 6\) đồng biến trên khoảng nào dưới đây? A. (3;4) B. (2;3) C. (1;4) D. (1;2) Câu 23: Cho đồ thị \(\left( P \right):\,\,y = {x^2} + 4x - 2\). Điểm nào dưới đây thuộc (P)? A. (1;-3) B. (3;18) C. (-2;-6) D. (-1;-4) Câu 24: Gọi \({m_0}\) là giá trị của m để hệ phương trình \(\left\{ \begin{array}{l}x + 3y = m\\mx + y = m - \dfrac{2}{9}\end{array} \right.\) có vô số nghiệm. Khi đó A. \({m_0} \in \left( {0;\dfrac{1}{2}} \right)\) B. \({m_0} \in \left( {\dfrac{1}{2};2} \right)\) C. \({m_0} \in \left( { - \dfrac{1}{2};0} \right)\) D. \({m_0} \in \left( { - 1; - \dfrac{1}{2}} \right)\) Câu 25: Gọi \({x_1};\,{x_2}\) là các nghiệm của phương trình \({x^2} + 4x - 15 = 0\). Tính \(\left| {{x_1} - {x_2}} \right|\). A. 8 B. \(\sqrt {76} \) C. 4 D. \(\sqrt {56} \) Câu 26: Đồ thị hàm số \(y = 3{x^2} + 4x - 1\) nhận đường thẳng nào dưới đây làm trục đối xứng? A. \(x = \dfrac{4}{3}\) B. \(y = \dfrac{2}{3}\) C. \(x = - \dfrac{2}{3}\) D. \(x = - \dfrac{1}{3}\) Câu 27: Tìm tập nghiệm của phương trình \(\sqrt {3{x^2} - 4x + 4} = 3x + 2\). A. \(\left\{ 0 \right\}\) B. \(\left\{ { - \dfrac{8}{3}} \right\}\) C. \(\left\{ { - \dfrac{8}{3};0} \right\}\) D. \(\emptyset \) Câu 28: Tọa độ đỉnh của parabol \(\left( P \right):\,\,y = - {x^2} + 2x - 3\) là: A. (1;-2) B. (-2;3) C. (-1;2) D. (2;-3) Câu 29: Phát biểu nào dưới đây là mệnh đề sai? A. 5 là ước của 125. B. 2020 chia hết cho 101. C. 9 là số chính phương. D. 91 là số nguyên tố. Câu 30: Cho tập hợp A = {0;1;2;3;4} và B = {0;2;4;6;8}. Hỏi tập hợp \(\left( {A\backslash B} \right) \cup \left( {B\backslash A} \right)\) có bao nhiêu phần tử? A. 7 B. 4 C. 10 D. 3 Câu 31: Đường thẳng đi qua hai điểm A(-1;4) và B(2;-7) có phương trình là: A. 3x + 11y – 1 = 0 B. 11x + 3y + 1 = 0 C. 11x + 3y – 1 = 0 D. 3x + 11y + 1 = 0 Câu 32: Tìm tập hợp tất cả các giá trị của tham số m để hàm số \(y = \sqrt {{x^2} + {m^2}} + \sqrt {{x^2} - m} \) có tập xác định là R. A. R \ {0} B. \(\left( {0; + \infty } \right)\) C. \(\left[ {0; + \infty } \right)\) D. \(\left( { - \infty ;0} \right]\) Câu 33: Trong mặt phẳng tọa độ Oxy, cho ba điểm A(-6;0), B(0;2) và C(-6;2). Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC. A. (-2;0) B. (-3;1) C. (3;-1) D. (-2;1) Câu 34: Tìm tập xác định của hàm số \(y = \sqrt {x + 2} - \dfrac{2}{{x - 3}}\). A. R\{3} B. \(\left( {3; + \infty } \right)\) C. \(\left( { - 2; + \infty } \right)\) D. \(\left( { - 2; + \infty } \right]\backslash \left\{ 3 \right\}\) Câu 35: Cho hình thoi ABCD có \(\angle BAD = {60^0}\) và BA = a. Gọi M, N lần lượt là trung điểm của AD, DC. Tính \(\overrightarrow {BM} .\overrightarrow {BN} \) bằng: A. \(\dfrac{{3\sqrt 3 {a^2}}}{8}\) B. \(\dfrac{{3{a^2}}}{8}\) C. \(\dfrac{{3{a^2}}}{4}\) D. \(\dfrac{{\sqrt 3 {a^2}}}{4}\) Câu 36: Cho phương trình \({x^3} + 3{x^2} + \left( {4{m^2} - 12m + 11} \right)x + {\left( {2m - 3} \right)^2} = 0.\) Tập hợp tất cả các giá trị của tham số m để phương trình có 3 nghiệm phân biệt. A. (1; 2) B. (–1; 1) C. (–2; –1) D. \(\left( { - \infty ;\,\,2} \right)\) Câu 37: Cho tam giác ABC, lấy các điểm M, N trên cạnh BC sao cho BM = MN = NC. Gọi \({G_1},\,\,{G_2}\) lần lượt là trọng tâm tam giác ABN, ACM. Biết rằng \(\overrightarrow {{G_1}{G_2}} \) được biểu diễn theo hai vecto \(\overrightarrow {AB} ,\,\,\overrightarrow {AC} \) dưới dạng \(\overrightarrow {{G_1}{G_2}} = x\overrightarrow {AB} + y\overrightarrow {AC} .\) Khi đó x + y bằng: A. \(\dfrac{4}{3}\) B. 1 C. \(\dfrac{2}{3}\) D. 0 Câu 38: Trong mặt phẳng tọa độ Oxy, cho các vecto \(\overrightarrow a = \left( {3; - 1} \right),\,\,\overrightarrow b = \left( {5; - 4} \right),\,\,\overrightarrow c = \left( {1; - 5} \right).\) Biết \(\overrightarrow c = x\overrightarrow a + y\overrightarrow b .\) Tính x + y. A. 2 B. –5 C. 4 D. –1 Câu 39: Cho hình chữ nhật ABCD có AB = a, AC = 2a. Tính góc giữa hai vecto \(\overrightarrow {CA} \) và \(\overrightarrow {DC} .\) A. \({120^0}\) B. \({60^0}\) C. \({150^0}\) D. \({45^0}\) Câu 40: Hàm số nào dưới đây đồng biến trên tập \(\mathbb{R}?\) A. \(y = - 2 + 3x\) B. \(y = \dfrac{2}{x}\) C. \(y = \sqrt {x + 3} \) D. \(y = - x + 2\) Câu 41: Cho hệ phương trình \(\left\{ \begin{array}{l}x - \left( {m + 1} \right)y = m - 2\\2mx + \left( {m - 2} \right)y = 4\end{array} \right.\). Biết rằng có hai giá trị của tham số m là m1và m2 để hệ phương trình có nghiệm \(\left( {{x_0};2} \right)\). Tính m1 + m2. A. \(\dfrac{2}{3}\) B. \(\dfrac{7}{3}\) C. \( - \dfrac{4}{3}\) D. \( - \dfrac{1}{3}\) Câu 42: Phương trình \(\left| {3 - x} \right| = \left| {2x - 5} \right|\) có hai nghiệm \({x_1},\,\,{x_2}.\) Tính \({x_1} + {x_2}.\) A. \( - \dfrac{{28}}{3}\) B. \(\dfrac{7}{3}\) C. \( - \dfrac{{14}}{3}\) D. \(\dfrac{{14}}{3}\) Câu 43: Có bao nhiêu giá trị nguyên của tham số m để phương trình \({\left( {{x^2} + 6x + 10} \right)^2} + m = 10{\left( {x + 3} \right)^2}\) có 4 nghiệm phân biệt? A. 13 B. 14 C. 15 D. 16 Câu 44: Trong mặt phẳng tọa độ Oxy, cho các điểm A(4; 3), B(0; –1), C(1;–2). Tìm tọa độ điểm M biết rằng vetco \( - 2\overrightarrow {MA} + 3\overrightarrow {MB} - 3\overrightarrow {MC} \) có tọa độ là (1; 7). A. (6; 5) B. (–2; –3) C. (3; –1) D. (1; –2) Câu 45: Cho phương trình \({x^2} + 2x - {m^2} = 0.\) Biết rằng có hai giá trị \({m_1},\,\,{m_2}\) của tham số m để phương trình có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^3 + x_2^3 + 10 = 0.\) Tính \({m_1}.{m_2}.\) A. \(\dfrac{3}{4}\) B. \( - \dfrac{1}{3}\) C. \( - \dfrac{3}{4}\) D. \(\dfrac{1}{3}\) Câu 46: Trong mặt phẳng tọa độ Oxy, cho các điểm \(A\left( {m; - 1} \right),\,\,B\left( {2;\,\,1 - 2m} \right),\,\,C\left( {3m + 1; - \dfrac{7}{3}} \right).\) Biết rằng có hai giá trị \({m_1},\,\,{m_2}\) của tham số m để A, B, C thẳng hàng. Tính \({m_1} + {m_2}.\) A. \( - \dfrac{1}{6}\) B. \( - \dfrac{4}{3}\) C. \(\dfrac{{13}}{6}\) D. \(\dfrac{1}{6}\) Câu 47: Gọi (a; b; c) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}5x + y + z = 5\\x - 3y + 2z = 11\\ - x + 2y + z = - 3\end{array} \right..\) Tính \({a^2} + {b^2} + {c^2}.\) A. 9 B. 16 C. 8 D. 14 Câu 48: Tìm tập nghiệm của phương trình \(\sqrt {4x + 1} + 5 = 0.\) A. \(\left\{ 2 \right\}\) B. \(\emptyset \) C. \(\left\{ { - \dfrac{1}{4}} \right\}\) D. \(\left\{ 6 \right\}\) Câu 49: Trong mặt phẳng với hệ trục tọa độ \(\left( {O;\,\,\overrightarrow i ;\,\,\overrightarrow j } \right)\) cho điểm M thỏa mãn \(\overrightarrow {OM} = - 2\overrightarrow i + 3\overrightarrow j .\) Tọa độ của M là: A. (2; –3) B. (–3; 2) C. (–2; 3) D. (3; –2) Câu 50: Gọi M, N lần lượt là trung điểm các cạnh CD, AB của hình bình hành ABCD. Tìm mệnh đề đúng trong các mệnh đề sau: A. \(\overrightarrow {AM} .\overrightarrow {DN} = \dfrac{1}{4}A{B^2} - A{D^2}\) B. \(\overrightarrow {AM} .\overrightarrow {DN} = \dfrac{1}{4}A{B^2} + A{D^2}\) C. \(\overrightarrow {AM} .\overrightarrow {DN} = A{B^2} - \dfrac{1}{4}A{D^2}\) D. \(\overrightarrow {AM} .\overrightarrow {DN} = A{B^2} + \dfrac{1}{4}A{D^2}\)
ĐÁP ÁN
HƯỚNG DẪN GIẢI CHI TIẾT Thực hiện: Ban chuyên môn Loigiahay.com
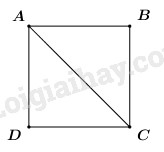
Câu 1 (NB) Phương pháp Hai phương trình tương đương là hai phương trình có cùng tập nghiệm. Hướng dẫn giải: Ta có: \({x^2} = 4 \Leftrightarrow \left| x \right| = 2\) \( \Rightarrow \) Đáp án A đúng. Đáp án A. Câu 2 (TH) Phương pháp Tứ giác ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \left\{ \begin{array}{l}{x_B} - {x_A} = {x_C} - {x_D}\\{y_B} - {y_A} = {y_C} - {y_D}\end{array} \right..\) Hướng dẫn giải: Gọi D(a; b). Khi đó ta có: ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \) \(\begin{array}{l} \Leftrightarrow \left( {1;\,\,6} \right) = \left( { - 1 - a;\,\,5 - b} \right)\\ \Leftrightarrow \left\{ \begin{array}{l} - 1 - a = 1\\5 - b = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 2\\b = - 1\end{array} \right. \Rightarrow D\left( { - 2; - 1} \right).\end{array}\) Đáp án C. Câu 3 (TH) Phương pháp Giải phương trình \(a{x^4} + b{x^2} + c = 0\,\,\,\left( {a \ne 0} \right)\) bằng cách đặt ẩn phụ: \(t = {x^2}\,\,\,\left( {t \ge 0} \right).\) Khi đó ta có phương trình \(a{t^2} + bt + c = 0.\) Giải phương trình bậc hai ẩn t sau đó tìm x. Hướng dẫn giải: Đặt \({x^2} = t\,\,\left( {t \ge 0} \right).\) Khi đó ta có phương trình: \(\begin{array}{l}{t^2} - 5t - 6 = 0 \Leftrightarrow \left( {t + 1} \right)\left( {t - 6} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}t + 1 = 0\\t - 6 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = - 1\,\,\left( {ktm} \right)\\t = 6\,\,\,\left( {tm} \right)\end{array} \right.\\ \Leftrightarrow {x^2} = 6 \Leftrightarrow \left[ \begin{array}{l}x = \sqrt 6 \\x = - \sqrt 6 \end{array} \right..\end{array}\) Vậy tập nghiệm của phương trình là:\(S = \left\{ { - \sqrt 6 ;\,\,\sqrt 6 } \right\}.\) Đáp án B. Câu 4 (TH) Phương pháp Thay các giá trị x = 5 và x = – 5 vào hàm số f (x) tương ứng rồi tính giá trị biểu thức. Hướng dẫn giải: Ta có:\(\left\{ \begin{array}{l}f\left( 5 \right) = \dfrac{{\sqrt {5 + 4} - 1}}{{5 - 1}} = \dfrac{1}{2}\\f\left( { - 5} \right) = 3 - \left( { - 5} \right) = 8\end{array} \right.\) \( \Rightarrow f\left( 5 \right) + f\left( { - 5} \right) = \dfrac{1}{2} + 8 = \dfrac{{17}}{2}.\) Đáp án C. Câu 5 (VDC): Phương pháp: Giải phương trình bằng cách chia cả 2 vế cho \(\sqrt[4]{{x - 2}}\sqrt[4]{{x + 2}}\). Hướng dẫn giải ĐK: \(\left\{ \begin{array}{l}x - 2 \ge 0\\x + 2 \ge 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\x \ge - 2\end{array} \right.\) \( \Leftrightarrow x \ge 2\) \( \Rightarrow D = \left[ {2; + \infty } \right)\). \(\begin{array}{l}\,\,\,\,\,4\sqrt {x - 2} + {m^2}\sqrt {x + 2} = 5\sqrt[4]{{{x^2} - 4}}\\ \Leftrightarrow 4\sqrt {x - 2} + {m^2}\sqrt {x + 2} = 5\sqrt[4]{{x - 2}}\sqrt[4]{{x + 2}}\end{array}\) TH1: \(x = 2\), phương trình trở thành: \(2{m^2} = 0 \Leftrightarrow m = 0\). Thử lại với \(m = 0\) ta có: \(\begin{array}{l}4\sqrt {x - 2} = 5\sqrt[4]{{x - 2}}\sqrt[4]{{x + 2}}\\ \Leftrightarrow \sqrt[4]{{x - 2}}\left( {4\sqrt[4]{{x - 2}} - 5\sqrt[4]{{x + 2}}} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\,\,\left( {tm} \right)\\4\sqrt[4]{{x - 2}} - 5\sqrt[4]{{x + 2}} = 0\end{array} \right.\end{array}\) Do đó phương trình có nghiệm \(x = 2\), suy ra \(m = 0\) thỏa mãn. TH2: \(x \ne 2\), chia cả 2 vế của phương trình cho \(\sqrt[4]{{x - 2}}\sqrt[4]{{x + 2}}\) ta được: \(4\dfrac{{\sqrt[4]{{x - 2}}}}{{\sqrt[4]{{x + 2}}}} + {m^2}\dfrac{{\sqrt[4]{{x + 2}}}}{{\sqrt[4]{{x - 2}}}} = 5\) Đặt \(\dfrac{{\sqrt[4]{{x - 2}}}}{{\sqrt[4]{{x + 2}}}} = t\,\,\left( {0 < t < 1} \right)\), phương trình trở thành \(4t + \dfrac{{{m^2}}}{t} = 5\)\( \Leftrightarrow 4{t^2} - 5t + {m^2} = 0\) (*) Phương trình (*) có nghiệm \( \Leftrightarrow \Delta = 25 - 16{m^2} \ge 0 \Leftrightarrow - \dfrac{5}{4} \le m \le \dfrac{5}{4}\). Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 1;0;1} \right\}\). Thử lại: Với \(m = \pm 1\) ta có: \(4{t^2} - 4t + 1 = 0 \Leftrightarrow t = \dfrac{1}{2}\). \(\begin{array}{l} \Rightarrow \dfrac{{\sqrt[4]{{x - 2}}}}{{\sqrt[4]{{x + 2}}}} = \dfrac{1}{2}\\ \Leftrightarrow 2\sqrt[4]{{x - 2}} = \sqrt[4]{{x + 2}}\\ \Leftrightarrow 16\left( {x - 2} \right) = x + 2\\ \Leftrightarrow 16x - 32 = x + 2\\ \Leftrightarrow 15x = 34\\ \Leftrightarrow x = \dfrac{{34}}{{15}}\,\,\left( {tm} \right)\end{array}\) \( \Rightarrow m = \pm 1\) thỏa mãn. Vậy có 3 giá trị nguyên của m thỏa mãn yêu cầu bài toán là \(m \in \left\{ { - 1;0;1} \right\}\). Đáp án B. Câu 6 (TH): Phương pháp: Sử dụng công thức \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ;\overrightarrow b } \right)\). Hướng dẫn giải
Vì ABCD là hình vuông cạnh a nên AB = BC = a và AC là phân giác của góc BAD. \( \Rightarrow \angle BAC = {45^0} = \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right)\). Áp dụng định lí Pytago trong tam giác vuông ABC ta có: \(\begin{array}{l}A{C^2} = A{B^2} + B{C^2}\\A{C^2} = {a^2} + {a^2} = 2{a^2}\\ \Rightarrow AC = a\sqrt 2 \end{array}\) Vậy \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right)\) \( = a.a\sqrt 2 .\cos {45^0}\)\( = {a^2}\sqrt 2 .\dfrac{{\sqrt 2 }}{2}\) \( = {a^2}\). Đáp án B. Câu 7 (TH): Phương pháp: Sử dụng các công thức cộng vectơ và nhân véctơ với 1 số. \(\begin{array}{l}\overrightarrow a = \left( {{x_1};{y_1}} \right);\,\,\overrightarrow b = \left( {{x_2};{y_2}} \right)\\ \Rightarrow k\overrightarrow a = \left( {k{x_1};k{y_1}} \right)\\\,\,\,\,\,\,\,\overrightarrow a + \overrightarrow b = \left( {{x_1} + {x_2};{y_1} + {y_2}} \right)\end{array}\) Hướng dẫn giải Ta có \(\begin{array}{l}2\overrightarrow u = \left( {2; - 4} \right)\\\,\,\,\overrightarrow v = \left( { - 2;2} \right)\\ \Rightarrow 2\overrightarrow u + \overrightarrow v = \left( {0; - 2} \right)\end{array}\) Đáp án C. Câu 8 (TH): Phương pháp: - Xác định tọa độ các vectơ \(\overrightarrow u ,\,\,\overrightarrow v \) như sau: \(\overrightarrow u = x\overrightarrow i + y\overrightarrow j \) \( \Rightarrow \overrightarrow u \left( {x;y} \right)\). - \(\overrightarrow u \bot \overrightarrow v \Leftrightarrow \overrightarrow u .\overrightarrow v = 0\). Hướng dẫn giải Ta có: \(\overrightarrow u = 2\overrightarrow i - 3\overrightarrow j \Rightarrow \overrightarrow u \left( {2; - 3} \right)\) và \(\overrightarrow v = k\overrightarrow i + \dfrac{1}{3}\overrightarrow j \Rightarrow \overrightarrow v \left( {k;\dfrac{1}{3}} \right)\). Vì \(\overrightarrow u \bot \overrightarrow v \) nên \(\overrightarrow u .\overrightarrow v = 0\) \(\begin{array}{l} \Leftrightarrow 2k - 3.\dfrac{1}{3} = 0\\ \Leftrightarrow 2k - 1 = 0\\ \Leftrightarrow k = \dfrac{1}{2}\end{array}\) Đáp án C. Câu 9 (TH): Phương pháp: Sử dụng quy tắc 3 điểm để cộng vectơ. Hướng dẫn giải
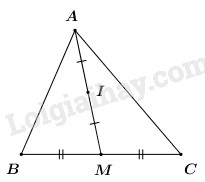
\(\begin{array}{l}\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} \\\overrightarrow {AM} = \overrightarrow {AB} + \dfrac{3}{4}\overrightarrow {BC} \\\overrightarrow {AM} = \overrightarrow {AB} + \dfrac{3}{4}\left( {\overrightarrow {BA} + \overrightarrow {AC} } \right)\\\overrightarrow {AM} = \overrightarrow {AB} - \dfrac{3}{4}\overrightarrow {AB} + \dfrac{3}{4}\overrightarrow {AC} \\\overrightarrow {AM} = \dfrac{1}{4}\overrightarrow {AB} + \dfrac{3}{4}\overrightarrow {AC} \end{array}\) Đáp án B. Câu 10 (TH): Phương pháp: - Đưa phương trình về dạng phương trình bậc nhất một ẩn: ax + b = 0. - Phương trình dạng ax + b = 0 có nghiệm \( \Leftrightarrow a \ne 0\). Hướng dẫn giải Ta có: \(\begin{array}{l}\,\,\,\,\,\,\left( {5{m^2} - 4} \right)x = 2m + x\\ \Leftrightarrow \left( {5{m^2} - 4} \right)x - 2m - x = 0\\ \Leftrightarrow \left( {5{m^2} - 5} \right)x - 2m = 0\end{array}\) Phương trình trên có nghiệm \(\begin{array}{l} \Leftrightarrow 5{m^2} - 5 \ne 0\\ \Leftrightarrow 5\left( {{m^2} - 1} \right) \ne 0\\ \Leftrightarrow {m^2} \ne 1\\ \Leftrightarrow m \ne \pm 1\end{array}\) Đáp án D. Câu 11 (TH): Phương pháp: - Xác định giá trị lớn nhất \(a\) của hàm số. - Phương trình \(a{x^2} + bx + c = m\) có \(VT \le 5\) vô nghiệm \( \Leftrightarrow m > 5\). Hướng dẫn giải \(\left( P \right):\,\,y = a{x^2} + bx + c\) có a < 0 và tọa độ đỉnh là (2;5) hàm số đạt giá trị lớn nhất bằng 5 khi x = 2. Do đó \(a{x^2} + bx + c \le 5\,\,\forall x\). Vậy phương trình \(a{x^2} + bx + c = m\) vô nghiệm khi và chỉ khi m > 5. Đáp án A. Câu 12 (NB): Phương pháp: Sử dụng quy tắc 3 điểm để cộng vectơ. Hướng dẫn giải Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {CA} } \right| = \left| {\overrightarrow {CA} + \overrightarrow {AB} } \right|\)\( = \left| {\overrightarrow {CB} } \right| = BC = a\). Đáp án A. Câu 13 (TH): Phương pháp: - Giải phương trình hoành độ giao điểm để tìm tọa độ các điểm A, B. - Gọi phương trình đường thẳng AB là y = ax + b. Thay tọa độ các điểm A, B vào và tìm a, b. Hướng dẫn giải Xét phương trình hoành độ giao điểm: \(\begin{array}{l}\,\,\,\,\,\,3{x^2} - 2 = 2{x^2} - x + 4\\ \Leftrightarrow {x^2} + x - 6 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 3\end{array} \right.\end{array}\) Với x = 2 thì y = 10 => A(2;10). Với x = -3 thì y = 25 => B(-3;25). Gọi phương trình đường thẳng AB là y = ax + b. Vì \(A \in AB\) nên 10 = 2a + b. Vì \(B \in AB\) nên 25 = -3a + b. Ta có hệ phương trình \(\left\{ \begin{array}{l}2a + b = 10\\ - 3a + b = 25\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 3\\b = 16\end{array} \right.\) Vậy phương trình đường thẳng AB là y = –3x + 16. Đáp án C. Câu 14 (NB): Phương pháp: Viết tập hợp A dưới dạng liệt kê các phần tử và đếm số phần tử của A. Hướng dẫn giải \(A = \left\{ {x \in \mathbb{Z}; - 3 < x \le 4} \right\}\) \( \Rightarrow A = \left\{ { - 2; - 1;0;1;2;3;4} \right\}\). Vậy tập hợp A có 7 phần tử. Đáp án B. Câu 15 (NB): Phương pháp: Tìm giao điểm của đồ thị hàm số với trục Oy ta cho x = 0. Hướng dẫn giải Cho x = 0 ta có: \(y = - {0^2} - 2.0 + 5 = 5\). Vậy giao điểm của (P) với Oy là (0;5). Đáp án A. Câu 16 (TH): Phương pháp: Sử dụng các đẳng thức vectơ liên quan đến trung điểm: - Nếu I là trung điểm của AB thì \(\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \). - Với mọi điểm M, I là trung điểm của AB thì \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \). Hướng dẫn giải
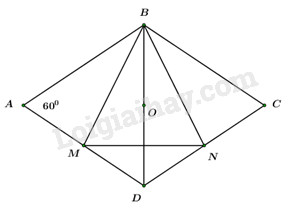
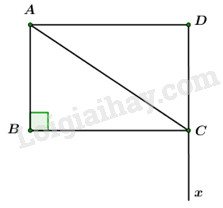
Vì I là trung điểm của AM nên \(\overrightarrow {IA} + \overrightarrow {IM} = \overrightarrow 0 \). Mà M là trung điểm của BC nên \(\overrightarrow {IB} + \overrightarrow {IC} = 2\overrightarrow {IM} \). Do đó \(\overrightarrow {IB} + \overrightarrow {IC} = -2\overrightarrow {IA} \) hay \(2\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \). Đáp án C. Câu 17 (NB): Phương pháp: Tập hợp có n phần tử thì có \({2^n}\) tập hợp con. Hướng dẫn giải Tập hợp A có 2 phần tử nên có \({2^2} = 4\) tập con. Đáp án A. Câu 18 (NB): Phương pháp: Hàm số bậc nhất có dạng y = ax + b với \(a \ne 0\). Hướng dẫn giải Hàm số \(y = \left( {m - 5} \right){x^2} - 5x + 1\) là hàm số bậc nhất \( \Leftrightarrow m - 5 = 0 \Leftrightarrow m = 5\). Đáp án A. Câu 19 (TH): Phương pháp: Cho hàm số y = f(x) có tập xác định là D. - Nếu \(\forall x \in D \Rightarrow - x \in D\) và f(-x) = f(x) thì hàm số là hàm số chẵn. - Nếu \(\forall x \in D \Rightarrow - x \in D\) và f(-x) = –f(x) thì hàm số là hàm số chẵn. Hướng dẫn giải Xét đáp án D ta có: TXĐ: D = R nên \(\forall x \in D \Rightarrow - x \in D\). Đặt \(y = f\left( x \right) = - {x^4} + 3{x^2} + 1\) ta có: \(\begin{array}{l}f\left( { - x} \right) = - {\left( { - x} \right)^4} + 3{\left( { - x} \right)^2} + 1\\f\left( { - x} \right) = - {x^4} + 3{x^2} + 1\\f\left( { - x} \right) = f\left( x \right)\end{array}\) Vậy hàm số \(y = - {x^4} + 3{x^2} + 1\) là hàm số chẵn. Đáp án D. Câu 20 (VD): Phương pháp: - Tìm điều kiện để phương trình hoành độ giao điểm có 2 nghiệm phân biệt. - Áp dụng định lí Vi-ét. Hướng dẫn giải Xét phương trình hoành độ giao điểm \({x^2} + 5x + 2m = 0\) (*). Để đồ thị hàm số \(y = {x^2} + 5x + 2m\) cắt trục Ox tại 2 điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt \( \Leftrightarrow \Delta = 25 - 8m > 0\) \( \Leftrightarrow m < \dfrac{{25}}{8}\). Gọi \({x_1};{x_2}\) là hai nghiệm phân biệt của phương trình (*) \( \Rightarrow A\left( {{x_1};0} \right)\) và \(B\left( {{x_2};0} \right)\). Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 5\\{x_1}{x_2} = 2m\end{array} \right.\) (**). Theo bài ra ta có: OA = 4OB \( \Leftrightarrow \left| {{x_1}} \right| = 4\left| {{x_2}} \right| \Leftrightarrow \left[ \begin{array}{l}{x_1} = 4{x_2}\\ - {x_1} = 4{x_2}\end{array} \right.\) TH1; \({x_1} = 4{x_2}\), thay vào hệ (**) ta có: \(\left\{ \begin{array}{l}{x_2} + 4{x_2} = 5\\{x_2}.4{x_2} = 2m\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_2} = 1\\4 = 2m\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_2} = 1\\m = 2\,\,\left( {tm} \right)\end{array} \right.\). TH2; \( - {x_1} = 4{x_2}\), thay vào hệ (**) ta có: \(\left\{ \begin{array}{l}{x_2} - 4{x_2} = 5\\{x_2}.\left( { - 4{x_2}} \right) = 2m\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_2} = - \dfrac{5}{3}\\ - \dfrac{{100}}{9} = 2m\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_2} = - \dfrac{5}{3}\\m = - \dfrac{{50}}{9}\,\,\left( {tm} \right)\end{array} \right.\). \( \Rightarrow S = \left\{ {2; - \dfrac{{50}}{9}} \right\}\). Vậy tổng các phần tử của S bằng \(2 + \left( { - \dfrac{{50}}{9}} \right) = - \dfrac{{32}}{9}\). Đáp án D. Câu 21 (TH): Phương pháp: - Thay tọa độ 2 điểm A và B vào hàm số, thiết lập hệ 2 phương trình 2 ẩn a, c. - Giải hệ phương trình tìm a và c. Hướng dẫn giải Vì A thuộc đồ thị hàm số nên \( - 2 = a - 1 + c \Leftrightarrow a + c = - 1\). Vì B thuộc đồ thị hàm số nên \(3 = 4a - 2 + c \Leftrightarrow 4a + c = 5\). Ta có hệ phương trình \(\left\{ \begin{array}{l}a + c = - 1\\4a + c = 5\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 2\\c = - 3\end{array} \right.\). Vậy \(y = 2{x^2} - x - 3\). Đáp án C. Câu 22 (TH): Phương pháp: Cho hàm số \(y = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\). - Nếu a > 0 thì hàm số đồng biến trên \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\). - Nếu a < 0 thì hàm số đồng biến trên \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\) và nghịch biến trên \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\). Hướng dẫn giải Hàm số \(y = - {x^2} + 5x - 6\) có \( - \dfrac{b}{{2a}} = - \dfrac{5}{{2.(-1)}} = \dfrac{5}{2}\) và \(a = - 1 < 0\) nên hàm số đồng biến trên \(\left( { - \infty ;\dfrac{5}{2}} \right)\) và nghịch biến trên \(\left( {\dfrac{5}{2}; + \infty } \right)\). Ta thấy \(\left( {1;2} \right) \subset \left( { - \infty ;\dfrac{5}{2}} \right)\) nên hàm số đồng biến trên (1;2). Đáp án D. Câu 23 (NB): Phương pháp: Thay tọa độ các điểm vào hàm số, điểm nào thỏa mãn thì sẽ thuộc đồ thị hàm số. Hướng dẫn giải Đáp án A: \({1^2} + 4.1 - 2 = 3 \ne - 3 \Rightarrow \left( {1; - 3} \right)\) không thuộc (P). Đáp án B: \({3^2} + 4.3 - 2 = 19 \ne 18 \Rightarrow \left( {3;18} \right)\) không thuộc (P). Đáp án C: \({\left( { - 2} \right)^2} + 4.\left( { - 2} \right) - 2 = - 6 \Rightarrow \left( { - 2; - 6} \right)\) thuộc (P). Đáp án C. Câu 24 (TH): Phương pháp: Hệ phương trình \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) có vô số nghiệm \( \Leftrightarrow \dfrac{a}{{a'}} = \dfrac{b}{{b'}} = \dfrac{c}{{c'}}\). Hướng dẫn giải Với m = 0, hệ phương trình trở thành \(\left\{ \begin{array}{l}x + 3y = 0\\y = - \dfrac{2}{9}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{2}{3}\\y = - \dfrac{2}{9}\end{array} \right.\). Hệ phương trình có nghiệm duy nhất nên m = 0 loại. Với \(m \ne 0\). Hệ phương trình \(\left\{ \begin{array}{l}x + 3y = m\\mx + y = m - \dfrac{2}{9}\end{array} \right.\) có vô số nghiệm \( \Leftrightarrow \dfrac{m}{1} = \dfrac{1}{3} = \dfrac{{m - \dfrac{2}{9}}}{m} \Leftrightarrow \left\{ \begin{array}{l}m = \dfrac{1}{3}\\{m^2} = m - \dfrac{2}{9}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m = \dfrac{1}{3}\\\left[ \begin{array}{l}m = \dfrac{2}{3}\\m = \dfrac{1}{3}\end{array} \right.\end{array} \right.\)\( \Leftrightarrow m = \dfrac{1}{3}\) (tm). Vậy \({m_0} = \dfrac{1}{3} \Rightarrow {m_0} \in \left( {0;\dfrac{1}{2}} \right)\). Đáp án A. Câu 25 (TH): Phương pháp: Sử dụng định lí Vi-ét và biến đổi \(\left| {{x_1} - {x_2}} \right| = \sqrt {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \). Hướng dẫn giải Do \({x_1};\,{x_2}\) là các nghiệm của phương trình \({x^2} + 4x - 15 = 0\) nên áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 4\\{x_1}{x_2} = - 15\end{array} \right.\). Vậy \(\left| {{x_1} - {x_2}} \right| = \sqrt {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \)\( = \sqrt {{{\left( { - 4} \right)}^2} - 4.\left( { - 15} \right)} \)\( = \sqrt {76} \). Đáp án B. Câu 26 (NB): Phương pháp: Đồ thị hàm số \(y = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\) nhận đường thẳng \(x = - \dfrac{b}{{2a}}\) làm trục đối xứng. Hướng dẫn giải Đồ thị hàm số \(y = 3{x^2} + 4x - 1\) nhận đường thẳng \(x = - \dfrac{4}{{2.3}} = - \dfrac{2}{3}\) làm trục đối xứng. Đáp án C. Câu 27 (VD): Phương pháp: Giải phương trình chứa căn: \(\sqrt A = B \Leftrightarrow \left\{ \begin{array}{l}B \ge 0\\A = {B^2}\end{array} \right.\). Hướng dẫn giải \(\begin{array}{l}\,\,\,\,\,\,\sqrt {3{x^2} - 4x + 4} = 3x + 2\\ \Leftrightarrow \left\{ \begin{array}{l}3x + 2 \ge 0\\3{x^2} - 4x + 4 = {\left( {3x + 2} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge - \dfrac{2}{3}\\3{x^2} - 4x + 4 = 9{x^2} + 12x + 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge - \dfrac{2}{3}\\6{x^2} + 16x = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge - \dfrac{2}{3}\\\left[ \begin{array}{l}x = - \dfrac{8}{3}\\x = 0\end{array} \right.\end{array} \right.\\ \Leftrightarrow x = 0\end{array}\) Vậy tập nghiệm của phương trình là \(S = \left\{ 0 \right\}\). Đáp án A. Câu 28 (NB): Phương pháp: \(\left( P \right):\,\,y = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\) có đỉnh \(I\left( { - \dfrac{b}{{2a}}; - \dfrac{\Delta }{{4a}}} \right)\). Hướng dẫn giải Hàm số \(\left( P \right):\,\,y = - {x^2} + 2x - 3\) có các hệ số \(a = - 1,\,\,\,b = 2,\,\,c = - 3\). \( \Rightarrow - \dfrac{b}{{2a}} = - \dfrac{2}{{2.\left( { - 1} \right)}} = 1\) và \( - \dfrac{\Delta }{{4a}} = - 2\). Vậy đỉnh của parabol là \(I\left( {1; - 2} \right)\). Đáp án A. Câu 29 (NB): Phương pháp: Nhận xét từng đáp án. Hướng dẫn giải Ta có 91 = 7.13 nên 91 là hợp số. Vậy đáp án D sai. Đáp án D. Câu 30 (TH): Phương pháp: - Tính \(A\backslash B = \left\{ {x|x \in A,\,\,x \notin B} \right\}\). - Tính \(B\backslash A = \left\{ {x|x \in B;\,\,x \notin A} \right\}\). - Tính \(\left( {A\backslash B} \right) \cup \left( {B\backslash A} \right) = \left\{ {x|x \in A\backslash B\,\,hoac\,\,x \in B\backslash A} \right\}\) Hướng dẫn giải Ta có: A \ B = {1;3} , B \ A = {6;8} \( \Rightarrow \left( {A\backslash B} \right) \cup \left( {B\backslash A} \right) = \left\{ {1;3;6;8} \right\}\). Vậy \(\left( {A\backslash B} \right) \cup \left( {B\backslash A} \right)\) có 4 phần tử. Đáp án B. Câu 31 (TH): Phương pháp: Gọi phương trình đường thẳng AB là y = ax + b. Thay tọa độ các điểm A, B vào và tìm a, b. Hướng dẫn giải Gọi phương trình đường thẳng AB là y = ax + b. Vì \(A \in AB\) nên 4 = –a + b. Vì \(B \in AB\) nên –7 = 2a + b. Ta có hệ phương trình \(\left\{ \begin{array}{l} - a + b = 4\\2a + b = - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \dfrac{{11}}{3}\\b = \dfrac{1}{3}\end{array} \right.\) Vậy phương trình đường thẳng AB là \(y = - \dfrac{{11}}{3}x + \dfrac{1}{3}\) \( \Leftrightarrow 3y = - 11x + 1\)\( \Leftrightarrow 11x + 3y - 1 = 0\). Đáp án C. Câu 32 (VD): Phương pháp: \(\sqrt A \) xác định \( \Leftrightarrow A \ge 0\). Hướng dẫn giải Hàm số xác định \( \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {m^2} \ge 0\,\,\\{x^2} - m \ge 0\end{array} \right. \Leftrightarrow {x^2} \ge m\). Để hàm số xác định trên R thì \({x^2} \ge m\,\,\forall x \in R\). Mà \({x^2} \ge 0\,\,\forall x \Rightarrow m \le 0\). Vậy \(m \in \left( { - \infty ;0} \right]\). Đáp án D. Câu 33 (VD): Phương pháp: - Gọi I là tâm đường tròn ngoại tiếp tam giác ABC thì IA = IB = IC. - Sử dụng công thức tính độ dài đoạn thẳng \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \). Hướng dẫn giải Gọi I(x;y) là tâm đường tròn ngoại tiếp tam giác ABC thì IA = IB = IC. \(\begin{array}{l} \Rightarrow I{A^2} = I{B^2} = I{C^2}\\ \Rightarrow \left\{ \begin{array}{l}I{A^2} = I{B^2}\\I{A^2} = I{C^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{\left( { - 6 - x} \right)^2} + {\left( { - y} \right)^2} = {\left( { - x} \right)^2} + {\left( {2 - y} \right)^2}\\{\left( { - 6 - x} \right)^2} + {\left( { - y} \right)^2} = {\left( { - 6 - x} \right)^2} + {\left( {2 - y} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x^2} + 12x + 36 + {y^2} = {x^2} + {y^2} - 4y + 4\\{y^2} = {y^2} - 4y + 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}12x + 4y = - 32\\ - 4y + 4 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = - 3\\y = 1\end{array} \right.\end{array}\) Vậy I(-3;1). Đáp án B. Câu 34 (TH): Phương pháp: \(\sqrt A \) xác định \( \Leftrightarrow A \ge 0\). \(\dfrac{1}{A}\) xác định \( \Leftrightarrow A \ne 0\). Hướng dẫn giải Hàm số xác định \( \Leftrightarrow \left\{ \begin{array}{l}x + 2 \ge 0\\x - 3 \ne 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge -2\\x \ne 3\end{array} \right.\). Vậy tập xác định của hàm số là \(D = \left( { - 2; + \infty } \right]\backslash \left\{ 3 \right\}\). Đáp án D. Câu 35 (VD) Phương pháp Sử dụng công thức tính tích vô hướng: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\,\,\overrightarrow b } \right).\) Hướng dẫn giải:
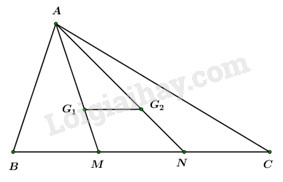
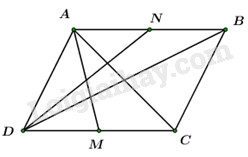
Ta có: ABCD là hình thoi có \(\angle BAD = {60^0}\)\( \Rightarrow \angle ABC = {120^0}\) và tam giác ABD là tam giác đều. \( \Rightarrow AB = AD = BD = a.\) Áp dụng quy tắc hình bình hành ta có: \(\left\{ \begin{array}{l}\overrightarrow {BM} = \dfrac{1}{2}\left( {\overrightarrow {BA} + \overrightarrow {BD} } \right)\\\overrightarrow {BN} = \dfrac{1}{2}\left( {\overrightarrow {BD} + \overrightarrow {BC} } \right)\end{array} \right..\) \(\begin{array}{l} \Rightarrow \overrightarrow {BM} .\overrightarrow {BN} = \dfrac{1}{4}\left( {\overrightarrow {BA} + \overrightarrow {BD} } \right)\left( {\overrightarrow {BD} + \overrightarrow {BC} } \right)\\ = \dfrac{1}{4}\left( {\overrightarrow {BA} .\overrightarrow {BD} + \overrightarrow {BA} .\overrightarrow {BC} + {{\overrightarrow {BD} }^2} + \overrightarrow {BD} .\overrightarrow {BC} } \right)\\ = \dfrac{1}{4}\left( {BA.BD.\cos ABD + BA.BC.\cos ABC + B{D^2} + BD.BC.\cos DBC} \right)\\ = \dfrac{1}{4}\left( {{a^2}.\cos {{60}^0} + {a^2}.\cos {{120}^0} + {a^2} + {a^2}.\cos {{60}^0}} \right)\\ = \dfrac{1}{4}\left( {\dfrac{{{a^2}}}{2} - \dfrac{{{a^2}}}{2} + {a^2} + \dfrac{{{a^2}}}{2}} \right) = \dfrac{{3{a^2}}}{8}.\end{array}\) Đáp án B. Câu 36 (VDC) Phương pháp Biến đổi phương trình đã cho về dạng:\(\left( {x - a} \right)g\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = a\\g\left( x \right) = 0\end{array} \right..\) Phương trình đã cho có 3 nghiệm phân biệt \( \Leftrightarrow g\left( x \right) = 0\) có hai nghiệm phân biệt \( \ne a.\) \( \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\g\left( a \right) \ne 0\end{array} \right..\) Hướng dẫn giải: \(\begin{array}{l}\,\,\,\,\,{x^3} + 3{x^2} + \left( {4{m^2} - 12m + 11} \right)x + {\left( {2m - 3} \right)^2} = 0\,\,\,\,\,\,\left( * \right)\\ \Leftrightarrow \,{x^3} + 3{x^2} + \left( {4{m^2} - 12m + 11} \right)x + 4{m^2} - 12m + 9 = 0\\ \Leftrightarrow {x^3} + {x^2} + 2{x^2} + 2x + \left( {4{m^2} - 12m + 9} \right)x + 4{m^2} - 12m + 9 = 0\\ \Leftrightarrow {x^2}\left( {x + 1} \right) + 2x\left( {x + 1} \right) + \left( {4{m^2} - 12m + 9} \right)\left( {x + 1} \right) = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} + 2x + 4{m^2} - 12m + 9} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = - 1\\g\left( x \right) = {x^2} + 2x + 4{m^2} - 12m + 9 = 0\end{array} \right.\end{array}\) Phương trình đã cho có 3 nghiệm phân biệt \( \Leftrightarrow g\left( x \right) = 0\) có hai nghiệm phân biệt \( \ne - 1\) \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\g\left( { - 1} \right) \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 - 4{m^2} + 12m - 9 > 0\\{\left( { - 1} \right)^2} + 2\left( { - 1} \right) + 4{m^2} - 12m + 9 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}4{m^2} - 12m + 8 < 0\\4{m^2} - 12m + 8 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 < m < 2\\m \ne 2\\m \ne 1\end{array} \right. \Leftrightarrow 1 < m < 2.\end{array}\) Đáp án A. Câu 37 (VD) Phương pháp Sử dụng các quy tắc vecto và các phép toán trên vecto để biến đổi và tìm x, y. Hướng dẫn giải:
Ta có:\({G_1}\) trọng tâm tam giác ABN \( \Rightarrow \overrightarrow {A{G_1}} = \dfrac{2}{3}\overrightarrow {AM} .\) \({G_2}\) trọng tâm tam giác ACM \( \Rightarrow \overrightarrow {A{G_2}} = \dfrac{2}{3}\overrightarrow {AN} .\) \(\begin{array}{l} \Rightarrow \overrightarrow {{G_1}{G_2}} = \overrightarrow {{G_1}A} + \overrightarrow {A{G_2}} = - \dfrac{2}{3}\overrightarrow {AM} + \dfrac{2}{3}\overrightarrow {AN} \\ = - \dfrac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {BM} } \right) + \dfrac{2}{3}\left( {\overrightarrow {AC} + \overrightarrow {CN} } \right)\\ = - \dfrac{2}{3}\overrightarrow {AB} - \dfrac{2}{3}.\dfrac{1}{3}\overrightarrow {BC} + \dfrac{2}{3}\overrightarrow {AC} - \dfrac{2}{3}.\dfrac{1}{3}\overrightarrow {BC} \\ = - \dfrac{2}{3}\overrightarrow {AB} + \dfrac{2}{3}\overrightarrow {AC} - \dfrac{4}{9}\overrightarrow {BC} \\ = - \dfrac{2}{3}\overrightarrow {AB} + \dfrac{2}{3}\overrightarrow {AC} - \dfrac{4}{9}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)\\ = - \dfrac{2}{3}\overrightarrow {AB} + \dfrac{2}{3}\overrightarrow {AC} - \dfrac{4}{9}\overrightarrow {AC} + \dfrac{4}{9}\overrightarrow {AB} \\ = - \dfrac{2}{9}\overrightarrow {AB} + \dfrac{2}{9}\overrightarrow {AC} .\\ \Rightarrow \left\{ \begin{array}{l}x = - \dfrac{2}{9}\\y = \dfrac{2}{9}\end{array} \right. \Rightarrow x + y = - \dfrac{2}{9} + \dfrac{2}{9} = 0.\end{array}\) Đáp án D. Câu 38 (VD) Phương pháp Cho các vecto \(\overrightarrow a = \left( {{a_1};\,\,{a_2}} \right),\,\,\overrightarrow b = \left( {{b_1};\,\,{b_2}} \right)\) và \(k \in \mathbb{R}\) ta có: \(\left\{ \begin{array}{l}\overrightarrow a + \overrightarrow b = \left( {{a_1} + {b_1};\,\,{a_2} + {b_2}} \right)\\k\overrightarrow a = k\left( {{a_1};\,\,{a_2}} \right) = \left( {k{a_1};\,\,k{a_2}} \right)\end{array} \right..\) Hướng dẫn giải: Ta có: \(\overrightarrow c = x\overrightarrow a + y\overrightarrow b \) \(\begin{array}{l} \Leftrightarrow \left( {1; - 5} \right) = x\left( {3; - 1} \right) + y\left( {5; - 4} \right)\\ \Leftrightarrow \left( {1; - 5} \right) = \left( {3x; - x} \right) + \left( {5y; - 4y} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}1 = 3x + 5y\\ - 5 = - x - 4y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 3\\y = 2\end{array} \right.\\ \Rightarrow x + y = - 3 + 2 = - 1.\end{array}\) Đáp án D. Câu 39 (TH) Phương pháp Sử dụng công thức tính góc giữa hai vecto: \(\cos \left( {\overrightarrow a ,\,\,\overrightarrow b } \right) = \dfrac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}.\) Hướng dẫn giải:
Ta có: ABCD là hình chữ nhật nên ta có: AB = DC = a. \(\begin{array}{l}\angle \left( {\overrightarrow {CA} ,\,\,\overrightarrow {DC} } \right) = \angle \left( {\overrightarrow {CA} ,\,\,\overrightarrow {Cx} } \right) = \angle ACx = {180^0} - \angle ACD.\\ \Rightarrow \cos \angle ACD = \dfrac{{CD}}{{AC}} = \dfrac{a}{{2a}} = \dfrac{1}{2}\\ \Rightarrow \angle ACD = {60^0}\\ \Rightarrow \angle ACx = {180^0} - {60^0} = {120^0}.\end{array}\) Đáp án A. Câu 40 (TH) Phương pháp Hàm số: \(y = ax + b\,\,\,\left( {a \ne 0} \right)\) đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0.\) Hướng dẫn giải: +) Xét đáp án A: \(y = - 2 + 3x\) có \(a = 3 > 0 \Rightarrow \) hàm số đồng biến trên \(\mathbb{R}.\) Đáp án A. Câu 41 (VD): Phương pháp: - Thay \(y = 2\) vào hệ phương trình. - Rút x từ phương trình thứ nhất thế vào phương trình thứ hai, rút ra phương trình bậc hai ẩn m. - Áp dụng định lí Vi-ét. Hướng dẫn giải Hệ phương trình có nghiệm \(\left( {{x_0};2} \right)\) nên thay \(y = 2\) ta có: \(\begin{array}{l}\left\{ \begin{array}{l}x - 2\left( {m + 1} \right) = m - 2\\2mx + 2\left( {m - 2} \right) = 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x - 2m - 2 = m - 2\\2mx + 2m - 4 = 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 3m\\2mx = 8 - 2m\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 3m\\2m.3m = 8 - 2m\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 3m\\6{m^2} + 2m - 8 = 0\,\,\left( 1 \right)\end{array} \right.\end{array}\) Hai giá trị của tham số m là nghiệm của phương trình (1), do đó áp dụng định lí Vi-ét ta có \({m_1} + {m_2} = \dfrac{{ - 1}}{3}\). Đáp án D. Câu 42 (VD) Phương pháp Giải phương trình chứa dấu giá trị tuyệt đối: \(\left| {f\left( x \right)} \right| = g\left( x \right) \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = g\left( x \right)\\f\left( x \right) = - g\left( x \right)\end{array} \right..\) Hướng dẫn giải: Ta có: \(\left| {3 - x} \right| = \left| {2x - 5} \right|\) \(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}3 - x = 2x - 5\\3 - x = - 2x + 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}3x = 8\\x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{8}{3}\\x = 2\end{array} \right.\\ \Rightarrow {x_1} + {x_2} = \dfrac{8}{3} + 2 = \dfrac{{14}}{3}.\end{array}\) Đáp án D. Câu 43 (VDC) Phương pháp Biến đổi phương trình, đặt ẩn phụ rồi biện luận phương trình. Hướng dẫn giải: TXĐ: \(D = \mathbb{R}.\) \(\begin{array}{l}\,\,\,\,\,\,{\left( {{x^2} + 6x + 10} \right)^2} + m = 10{\left( {x + 3} \right)^2}\,\,\,\,\\ \Leftrightarrow {\left( {{x^2} + 6x + 9 + 1} \right)^2} - 10{\left( {x + 3} \right)^2} + m = 0\\ \Leftrightarrow {\left[ {{{\left( {x + 3} \right)}^2} + 1} \right]^2} - 10{\left( {x + 3} \right)^2} + m = 0\\ \Leftrightarrow {\left( {x + 3} \right)^4} + 2{\left( {x + 3} \right)^2} + 1 - 10{\left( {x + 3} \right)^2} + m = 0\\ \Leftrightarrow {\left( {x + 3} \right)^4} - 8{\left( {x + 3} \right)^2} + m + 1 = 0\,\,\,\,\,\left( * \right)\end{array}\) Đặt \({\left( {x + 3} \right)^2} = t\,\,\left( {t \ge 0} \right).\) \( \Rightarrow \left( * \right) \Leftrightarrow {t^2} - 8t + m + 1 = 0\,\,\,\,\left( 1 \right)\) \( \Rightarrow \left( * \right)\) có 4 nghiệm phân biệt \( \Leftrightarrow \left( 1 \right)\) có hai nghiệm t dương phân biệt \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\ - \dfrac{b}{a} > 0\\\dfrac{c}{a} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}16 - m - 1 > 0\\8 > 0\\m + 1 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}15 - m > 0\\m > - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 15\\m > - 1\end{array} \right. \Leftrightarrow - 1 < m < 15\end{array}\) Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;\,\,1;\,\,2;\,\,.....;\,\,14} \right\}.\) \( \Rightarrow \) Có 15 giá trị m thỏa mãn bài toán. Đáp án C. Câu 44 (VD) Phương pháp Cho các vecto \(\overrightarrow a = \left( {{a_1};\,\,{a_2}} \right),\,\,\overrightarrow b = \left( {{b_1};\,\,{b_2}} \right)\) và \(k \in \mathbb{R}\) ta có: \(\left\{ \begin{array}{l}\overrightarrow a + \overrightarrow b = \left( {{a_1} + {b_1};\,\,{a_2} + {b_2}} \right)\\k\overrightarrow a = k\left( {{a_1};\,\,{a_2}} \right) = \left( {k{a_1};\,\,k{a_2}} \right)\end{array} \right..\) Hướng dẫn giải: Gọi M (a; b). \(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\overrightarrow {MA} = \left( {4 - a;\,\,3 - b} \right)\\\overrightarrow {MB} = \left( { - a; - 1 - b} \right)\\\overrightarrow {MC} = \left( {1 - a; - 2 - b} \right)\end{array} \right. \\\Rightarrow - 2\overrightarrow {MA} + 3\overrightarrow {MB} - 3\overrightarrow {MC} = \left( {1;\,\,7} \right)\\ \Leftrightarrow - 2\left( {4 - a;\,\,3 - b} \right) + 3\left( { - a; - 1 - b} \right) - 3\left( {1 - a; - 2 - b} \right) = \left( {1;\,\,7} \right)\\ \Leftrightarrow \left\{ \begin{array}{l} - 2\left( {4 - a} \right) + 3\left( { - a} \right) - 3\left( {1 - a} \right) = 1\\ - 2\left( {3 - b} \right) + 3\left( { - 1 - b} \right) - 3\left( { - 2 - b} \right) = 7\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 8 + 2a - 3a - 3 + 3a = 1\\ - 6 + 2b - 3 - 3b + 6 + 3b = 7\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}2a = 12\\2b = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 6\\b = 5\end{array} \right. \Rightarrow M\left( {6;\,\,5} \right).\end{array}\) Đáp án A. Câu 45 (VD) Phương pháp Tìm điều kiện của m để phương trình có hai nghiệm phân biệt. Áp dụng định lý Vi-et để tính giá trị biểu thức, từ đó xác định giá trị của m. Hướng dẫn giải: Phương trình đã cho có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0\) \( \Leftrightarrow 1 + {m^2} > 0\,\,\,\forall m\) \( \Rightarrow \) Phương trình đã cho luôn có hai nghiệm phân biệt \({x_1},\,{x_2}\) với mọi m. Áp dụng định lý Vi-et ta có:\(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2\\{x_1}{x_2} = - {m^2}\end{array} \right..\) Theo đề bài ta có: \(x_1^3 + x_2^3 + 10 = 0\) \(\begin{array}{l} \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right) + 10 = 0\\ \Leftrightarrow {\left( { - 2} \right)^3} - 3\left( { - {m^2}} \right)\left( { - 2} \right) + 10 = 0\\ \Leftrightarrow - 8 - 6{m^2} + 10 = 0\\ \Leftrightarrow 6{m^2} = 2 \Leftrightarrow {m^2} = \dfrac{1}{3}\\ \Leftrightarrow \left[ \begin{array}{l}{m_1} = - \dfrac{1}{{\sqrt 3 }}\\{m_2} = \dfrac{1}{{\sqrt 3 }}\end{array} \right. \Rightarrow {m_1}{m_2} = - \dfrac{1}{{\sqrt 3 }}.\dfrac{1}{{\sqrt 3 }} = - \dfrac{1}{3}.\end{array}\) Đáp án B. Câu 46 (VD) Phương pháp Ba điểm A, B, C thẳng hàng \( \Leftrightarrow \overrightarrow {AB} = k\overrightarrow {AC} \,\,\,\left( {k \in \mathbb{R},\,\,k \ne 0} \right).\) Hướng dẫn giải: Ta có: \(\left\{ \begin{array}{l}\overrightarrow {AB} = \left( {2 - m;\,\,2 - 2m} \right)\\\overrightarrow {AC} = \left( {2m + 1;\,\, - \dfrac{4}{3}} \right)\end{array} \right..\) Ba điểm A, B, C thẳng hàng \( \Leftrightarrow \overrightarrow {AB} = k\overrightarrow {AC} \,\,\,\left( {k \in \mathbb{R},\,\,k \ne 0} \right)\) \(\begin{array}{l} \Leftrightarrow \left( {2 - m;\,\,2 - 2m} \right) = k\left( {2m + 1; - \dfrac{4}{3}} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}2 - m = k\left( {2m + 1} \right)\\2 - 2m = - \dfrac{4}{3}k\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k = \dfrac{{3\left( {m - 1} \right)}}{2}\\2 - m = \dfrac{{3\left( {m - 1} \right)}}{2}\left( {2m + 1} \right)\,\,\,\,\left( * \right)\end{array} \right.\\ \Rightarrow \left( * \right) \Leftrightarrow 4 - 2m = 6{m^2} + 3m - 6m - 3\\ \Leftrightarrow 6{m^2} - m - 7 = 0\\ \Leftrightarrow \left( {6m - 7} \right)\left( {m + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}6m - 7 = 0\\m + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{7}{6}\\m = - 1\end{array} \right.\\ \Rightarrow {m_1} + {m_2} = \dfrac{7}{6} - 1 = \dfrac{1}{6}.\end{array}\) Đáp án D. Câu 47 (TH) Phương pháp Giải hệ phương trình bậc nhất ba ẩn sau đó tính giá trị của biểu thức. Hướng dẫn giải: Ta có: \(\left\{ \begin{array}{l}5x + y + z = 5\\x - 3y + 2z = 11\\ - x + 2y + z = - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 2\\z = 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 1\\b = - 2\\c = 2\end{array} \right.\)\( \Rightarrow {a^2} + {b^2} + {c^2} = {1^2} + {\left( { - 2} \right)^2} + {2^2} = 9.\) Đáp án A. Câu 48 (TH) Phương pháp Giải phương trình chứa căn bậc hai. Hướng dẫn giải: Điều kiện: \(4x + 1 \ge 0 \Leftrightarrow x \ge - \dfrac{1}{4}.\) Ta có: \(\sqrt {4x + 1} \ge 0\,\,\forall x \ge - \dfrac{1}{4}\) \( \Rightarrow \sqrt {4x + 1} + 5 > 0\,\,\forall x \ge - \dfrac{1}{4}\) \( \Rightarrow \) Phương trình đã cho vô nghiệm. Đáp án B. Câu 49 (TH) Phương pháp Cho vetco \(\overrightarrow u = a\overrightarrow i + b\overrightarrow j \Rightarrow \overrightarrow u = \left( {a;\,\,b} \right).\) Hướng dẫn giải: Ta có: \(\overrightarrow {OM} = - 2\overrightarrow i + 3\overrightarrow j \Rightarrow \overrightarrow {OM} = \left( { - 2;\,\,3} \right) \Rightarrow M\left( { - 2;\,\,3} \right).\) Đáp án C. Câu 50 (VDC) Phương pháp Sử dụng các quy tắc hình bình hành và công thức tính tích vô hướng. Hướng dẫn giải:
\(\begin{array}{l}\overrightarrow {AM} .\overrightarrow {DN} = \left( {\overrightarrow {AD} + \overrightarrow {DM} } \right)\left( {\overrightarrow {DA} + \overrightarrow {AN} } \right)\\ = \overrightarrow {AD} .\overrightarrow {DA} + \overrightarrow {DM} .\overrightarrow {DA} + \overrightarrow {AD} .\overrightarrow {AN} + \overrightarrow {DM} .\overrightarrow {AN} \\ = - A{D^2} + \dfrac{1}{2}\overrightarrow {DC} .\overrightarrow {DA} + \overrightarrow {AD} .\dfrac{1}{2}\overrightarrow {AB} + \dfrac{1}{2}\overrightarrow {DC} .\dfrac{1}{2}\overrightarrow {AB} \\ = - A{D^2} + \dfrac{1}{2}\overrightarrow {AB} .\overrightarrow {DA} + \dfrac{1}{2}\overrightarrow {AD} .\overrightarrow {AB} + \dfrac{1}{4}DC.AB.\cos {0^0}\\ = - A{D^2} + \dfrac{1}{4}A{B^2}\\ = \dfrac{1}{4}A{B^2} - A{D^2}.\end{array}\) Đáp án A. HocTot.XYZ
|