Đề thi học kì 1 môn toán lớp 10 năm 2019 - 2020 trường THPT Đống ĐaGiải chi tiết đề thi học kì 1 môn toán lớp 10 năm 2019 - 2020 trường THPT Đống Đa với cách giải nhanh và chú ý quan trọng Câu 1 (3,0 điểm). 1) Lập bảng biến thiên và vẽ đồ thị \(\left( P \right)\) của hàm số \(y = {x^2}{\rm{ + }}2x-3\) 2) Tìm tọa độ giao điểm của \(\left( P \right)\)và đường thẳng \(d:{\rm{ }}y{\rm{ }} = {\rm{ }}x{\rm{ }}-{\rm{ }}1\) 3) Tìm \(m\) sao cho đường thẳng \(y{\rm{ }} = {\rm{ }}2m\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ âm. Câu 2 (3,5 điểm). Giải các phương trình sau : \(1)\,\left( {{x^2} - 7x + 10} \right)\sqrt {4 - x} = 0\) \(2)\,\left| {{x^2} - 5x + 5} \right| = x - 3\) \(3)\,\sqrt {2x + 3} = 2 + \sqrt {x - 2} \) Câu 3 (0,5 điểm). Tìm \(m\) sao cho phương trình sau có đúng \(2\) nghiệm : \(4{x^2} - 8x + 22 = 3m + 12\sqrt {2{x^2} - 4x + 6} \) Câu IV (3,0 điểm) Trong mặt phẳng tọa độ \(Oxy\) cho tam giác \(ABC\) có \(A\left( {1; - 1} \right),\,B\left( {4; - 3} \right)\) và \(C\left( {5;5} \right).\) 1) Chứng minh rằng tam giác \(ABC\) vuông tại \(A\) và tính diện tích tam giác \(ABC.\) 2) Tìm điểm \(D\) trên trục hoành sao cho ba điểm \(A,\,B,\,D\) thẳng hàng. 3) Tìm điểm \(M\) trên đường thẳng \(d:y = 2x - 1\) sao cho \(M{A^2} + M{B^2} + M{C^2}\) đạt giá trị nhỏ nhất. ----------HẾT----------
HƯỚNG DẪN GIẢI CHI TIẾT Thực hiện: Ban chuyên môn HocTot.XYZ
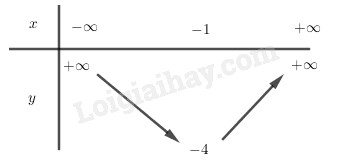
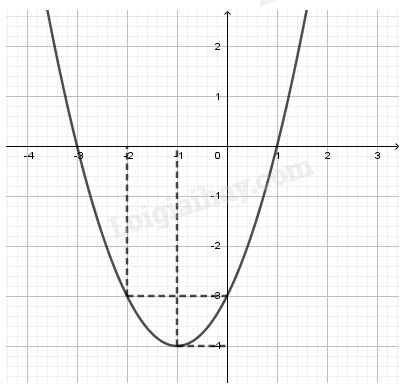
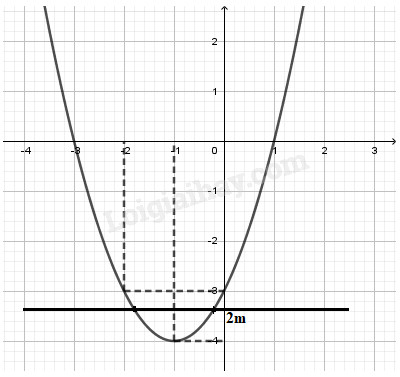
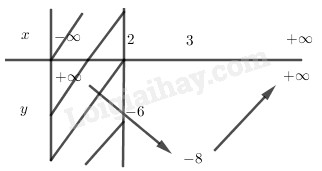
Câu 1 (VD): Phương pháp: a) Tìm hoành độ đỉnh, trục đối xứng của Parabol, từ đó suy ra khoảng đồng biến nghịch biến và lập bảng biến thiên. b) Xét phương trình hoành độ giao điểm tìm nghiệm. c) Nhận xét điều kiện từ đồ thị đã vẽ. Cách giải: 1) Lập bảng biến thiên và vẽ đồ thị \(\left( P \right)\) của hàm số \(y = {x^2} + 2x-3\) Ta có: \( - \dfrac{b}{{2a}} = - \dfrac{2}{{2.1}} = - 1, - \dfrac{\Delta }{{4a}} = - 4\) Vì \(a = 1 > 0\) nên hàm số nghịch biến trên \(\left( { - \infty ; - 1} \right)\) và đồng biến trên \(\left( { - 1; + \infty } \right)\). Bảng biến thiên: Đồ thị: Đỉnh \(P\left( { - 1; - 4} \right)\), cắt \(Ox\) tại \(\left( {1;0} \right),\left( { - 3;0} \right)\), cắt \(Oy\) tại \(\left( {0; - 3} \right)\), đi qua điểm \(\left( { - 2; - 3} \right)\). Trục đối xứng \(x = - 1\), bề lõm hướng lên trên. 2) Tìm tọa độ giao điểm của \(\left( P \right)\)và đường thẳng \(d:{\rm{ }}y{\rm{ }} = {\rm{ }}x{\rm{ }}-{\rm{ }}1\) Xét phương trình hoành độ giao điểm \({x^2} + 2x - 3 = x - 1\) \( \Leftrightarrow {x^2} + x - 2 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 1,y = 0\\x = - 2,y = - 3\end{array} \right.\) Vậy giao điểm là \(A\left( {1;0} \right),B\left( { - 2; - 3} \right)\). 3) Tìm \(m\) sao cho đường thẳng \(y{\rm{ }} = {\rm{ }}2m\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ âm. Đường thẳng \(y = 2m\) đi qua điểm \(\left( {0;2m} \right)\) và song song hoặc trùng với trục hoành. Từ đồ thị ta thấy YCBT thỏa mãn khi \( - 4 < 2m < - 3 \Leftrightarrow - 2 < m < - \dfrac{3}{2}\). Vậy \( - 2 < m < - \dfrac{3}{2}\). Câu 2 (VD): Phương pháp: 1) Giải phương trình tích \(AB = 0 \Leftrightarrow \left[ \begin{array}{l}A = 0\\B = 0\end{array} \right.\) 2) Bình phương hai vế chú ý điều kiện. 3) Bình phương hai vế chú ý điều kiện. Cách giải: \(1)\,\left( {{x^2} - 7x + 10} \right)\sqrt {4 - x} = 0\) ĐK: \(4 - x \ge 0 \Leftrightarrow x \le 4\) Khi đó PT\( \Leftrightarrow \left[ \begin{array}{l}{x^2} - 7x + 10 = 0\\4 - x = 0\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}\left( {x - 2} \right)\left( {x - 5} \right) = 0\\4 - x = 0\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = 2\left( {TM} \right)\\x = 5\left( {KTM} \right)\\x = 4\left( {TM} \right)\end{array} \right.\) Vậy phương trình có tập nghiệm \(S = \left\{ {4;2} \right\}\). \(2)\,\left| {{x^2} - 5x + 5} \right| = x - 3\) \( \Leftrightarrow \left\{ \begin{array}{l}x - 3 \ge 0\\{\left( {{x^2} - 5x + 5} \right)^2} = {\left( {x - 3} \right)^2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left( {{x^2} - 5x + 5 - x + 3} \right)\left( {{x^2} - 5x + 5 + x - 3} \right) = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left( {{x^2} - 6x + 8} \right)\left( {{x^2} - 4x + 2} \right) = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left[ \begin{array}{l}{x^2} - 6x + 8 = 0\\{x^2} - 4x + 2 = 0\end{array} \right.\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left[ \begin{array}{l}x = 2,x = 4\\x = 2 \pm \sqrt 2 \end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = 2 + \sqrt 2 \end{array} \right.\) Vậy phương trình có tập nghiệm \(S = \left\{ {4;2 + \sqrt 2 } \right\}\). \(3)\,\sqrt {2x + 3} = 2 + \sqrt {x - 2} \) ĐK: \(\left\{ \begin{array}{l}2x + 3 \ge 0\\x - 2 \ge 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge - \dfrac{3}{2}\\x \ge 2\end{array} \right. \Leftrightarrow x \ge 2\) PT\( \Leftrightarrow 2x + 3 = 4 + 4\sqrt {x - 2} + x - 2\) \( \Leftrightarrow x + 1 = 4\sqrt {x - 2} \) \( \Leftrightarrow {\left( {x + 1} \right)^2} = 16\left( {x - 2} \right)\) \( \Leftrightarrow {x^2} + 2x + 1 = 16x - 32\) \( \Leftrightarrow {x^2} - 14x + 33 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 11\\x = 3\end{array} \right.\left( {TM} \right)\) Vậy phương trình có tập nghiệm \(S = \left\{ {11;3} \right\}\). Câu 3 (VDC): Phương pháp: - Đặt ẩn phụ \(t = \sqrt {2{x^2} - 4x + 6} \), tìm điều kiện của \(t\). - Biến đổi phương trình về dạng \(3m = f\left( t \right)\) rồi dùng phương pháp hàm số tìm điều kiện của \(m\). Cách giải: Tìm \(m\) sao cho phương trình sau có đúng \(2\) nghiệm :\(4{x^2} - 8x + 22 = 3m + 12\sqrt {2{x^2} - 4x + 6} \) Đặt \(t = \sqrt {2{x^2} - 4x + 6} \ge 0\) ta có: \(2{x^2} - 4x + 6 = 2\left( {{x^2} - 2x + 1} \right) + 4\) \( = 2{\left( {x - 1} \right)^2} + 4 \ge 4\) \( \Rightarrow {t^2} \ge 4 \Rightarrow t \ge 2\) Khi đó phương trình trở thành \(2{t^2} + 10 = 3m + 12t\) \( \Leftrightarrow 2{t^2} - 12t + 10 = 3m\,\left( 1 \right)\) Ứng với mỗi một giá trị \(t > 2\) thì có hai giá trị của \(x\), do đó yêu cầu bài toán thỏa khi \(\left( 1 \right)\) có nghiệm duy nhất \(t > 2\). Xét hàm số \(f\left( t \right) = 2{t^2} - 12t + 10\) với \(t \ge 2\). Ta có: \( - \dfrac{b}{{2a}} = - \dfrac{{ - 12}}{{2.2}} = 3\), \( - \dfrac{\Delta }{{4a}} = - 8\). Vì \(a = 2 > 0\) nên hàm số đồng biến trên \(\left( {3; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ;3} \right)\). Bảng biến thiên: Đường thẳng \(y = 3m\) đi qua điểm \(\left( {0;3m} \right)\) và song song hoặc trùng với trục hoành tại điểm \(\left( {0;3m} \right)\). Phương trình (1) có nghiệm duy nhất \(t > 2\) \( \Leftrightarrow \) đường thẳng \(y = 3m\) cắt đồ thị hàm số \(f\left( t \right)\) tại điểm duy nhất \(t > 2\) \( \Leftrightarrow \left[ \begin{array}{l}3m > - 6\\3m = - 8\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m > - 2\\m = - \dfrac{8}{3}\end{array} \right.\). Vậy \(\left[ \begin{array}{l}m > - 2\\m = - \dfrac{8}{3}\end{array} \right.\). Câu 4 (VD ): Phương pháp: 1) Tích tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} \). 2) Ba điểm \(A,B,D\) thẳng hàng nếu \(\overrightarrow {AB} ,\overrightarrow {AD} \) cùng phương. 3) Gọi \(M\left( {a;2a - 1} \right) \in d\), tính \(M{A^2} + M{B^2} + M{C^2}\) theo \(a\) và tìm GTNN. Cách giải: 1) Chứng minh rằng tam giác \(ABC\) vuông tại \(A\) và tính diện tích tam giác \(ABC.\) Ta có: \(\overrightarrow {AB} = \left( {3; - 2} \right)\) \( \Rightarrow AB = \sqrt {{3^2} + {{\left( { - 2} \right)}^2}} = \sqrt {13} \) \(\overrightarrow {AC} = \left( {4;6} \right)\) \( \Rightarrow AC = \sqrt {{4^2} + {6^2}} = 2\sqrt {13} \) \(\overrightarrow {AB} .\overrightarrow {AC} = 3.4 - 2.6 = 0\) nên \(AB \bot AC\) hay \(ABC\) là tam giác vuông tại \(A\). Diện tích \({S_{\Delta ABC}} = \dfrac{1}{2}AB.AC\) \( = \dfrac{1}{2}.\sqrt {13} .2\sqrt {13} = 13\). 2) Tìm điểm \(D\) trên trục hoành sao cho ba điểm \(A,\,B,\,D\) thẳng hàng. Gọi \(D\left( {x;0} \right) \in Ox\)\( \Rightarrow \overrightarrow {AD} = \left( {x - 1;1} \right)\),\(\overrightarrow {AB} = \left( {3; - 2} \right)\) \(A,B,D\) thẳng hàng \( \Leftrightarrow \overrightarrow {AB} ,\overrightarrow {AD} \) cùng phương \( \Leftrightarrow \dfrac{{x - 1}}{3} = \dfrac{1}{{ - 2}}\) \( \Leftrightarrow - 2x + 2 = 3 \Leftrightarrow x = - \dfrac{1}{2}\). Vậy \(D\left( { - \dfrac{1}{2};0} \right)\). 3) Tìm điểm \(M\) trên đường thẳng \(d:y = 2x - 1\) sao cho \(M{A^2} + M{B^2} + M{C^2}\) đạt giá trị nhỏ nhất. Gọi \(M\left( {a;2a - 1} \right) \in d\) ta có: \(\overrightarrow {MA} = \left( {1 - a; - 2a} \right)\)\( \Rightarrow M{A^2} = {\left( {1 - a} \right)^2} + {\left( { - 2a} \right)^2}\) \( = 1 - 2a + {a^2} + 4{a^2}\) \( = 5{a^2} - 2a + 1\) \(\overrightarrow {MB} = \left( {4 - a; - 2 - 2a} \right)\)\( \Rightarrow M{A^2} = {\left( {4 - a} \right)^2} + {\left( { - 2 - 2a} \right)^2}\) \( = 16 - 8a + {a^2} + 4 + 8a + 4{a^2}\) \( = 5{a^2} + 20\) \(\overrightarrow {MC} = \left( {5 - a;6 - 2a} \right)\)\( \Rightarrow M{A^2} = {\left( {5 - a} \right)^2} + {\left( {6 - 2a} \right)^2}\) \( = 25 - 10a + {a^2} + 36 + 24a + 4{a^2}\)\( = 5{a^2} + 14a + 61\) \( \Rightarrow M{A^2} + M{B^2} + M{C^2}\) \( = 5{a^2} - 2a + 1 + 5{a^2} + 20 + 5{a^2} + 14a + 61\) \( = 15{a^2} + 12a + 82\) \( = 15\left( {{a^2} + \dfrac{4}{5}a + \dfrac{4}{{25}}} \right) + \dfrac{{398}}{5}\) \( = 15{\left( {a + \dfrac{2}{5}} \right)^2} + \dfrac{{398}}{5} \ge \dfrac{{398}}{5}\) Do đó \({\left( {M{A^2} + M{B^2} + M{C^2}} \right)_{\min }} = \dfrac{{398}}{5}\) khi \(a + \dfrac{2}{5} = 0 \Leftrightarrow a = - \dfrac{2}{5}\) \( \Rightarrow 2a - 1 = - \dfrac{9}{5}\) Vậy \(M\left( { - \dfrac{2}{5}; - \dfrac{9}{5}} \right)\). HocTot.XYZ
|