Giải mục 1 trang 47, 48, 49, 50 Chuyên đề học tập Toán 10 - Kết nối tri thứcTrong mặt phẳng tọa độ, cho hypebol có phương trình chính tắc
Lựa chọn câu để xem lời giải nhanh hơn
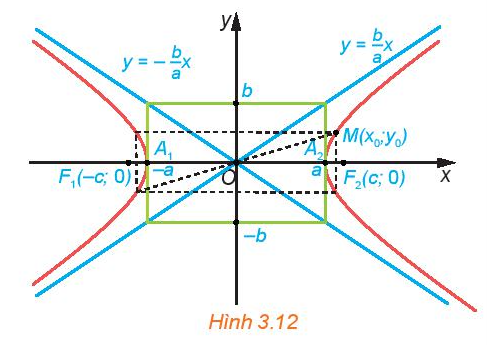
HĐ1 Trong mặt phẳng tọa độ, cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\). a) Hãy giải thích vì sao, nếu điểm \(M({x_0};{y_0})\) thuộc hypebol thì các điểm có tọa độ \(({x_0}; - {y_0}),( - {x_0};{y_0}),( - {x_0}; - {y_0})\) cũng thuộc hypebol (H.3.12). b) Tìm tọa độ các giao điểm của hypebol với trục hoành. Hypebol có cắt trục tung hay không? Vì sao? c) Với điểm \(M({x_0};{y_0})\) thuộc hypebol, hãy so sánh \(\left| {{x_0}} \right|\) với \(a\)
Lời giải chi tiết: a) Nếu điểm \(M({x_0};{y_0})\) thuộc hypebol thì \(\frac{{{x_0}^2}}{{{a^2}}} - \frac{{{y_0}^2}}{{{b^2}}} = 1\) \( \Rightarrow \frac{{{x_0}^2}}{{{a^2}}} - \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} - \frac{{{y_0}^2}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} - \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1\) hay các điểm có tọa độ \(({x_0}; - {y_0}),( - {x_0};{y_0}),( - {x_0}; - {y_0})\) cũng thuộc Hypebol. b) \(y = 0 \Rightarrow \frac{{{x^2}}}{{{a^2}}} = 1 \Rightarrow x = \pm a\) Giao điểm của hypebol với Ox là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right).\) \(x = 0 \Rightarrow - \frac{{{y^2}}}{{{b^2}}} = 1\) Vô lý vì \( - \frac{{{y^2}}}{{{b^2}}} \le 0 < 1\) Vậy hypebol không có giao điểm với trục tung. c) \(M({x_0};{y_0})\) thuộc hypebol thì \(\frac{{{x_0}^2}}{{{a^2}}} - \frac{{{y_0}^2}}{{{b^2}}} = 1\) \(\begin{array}{l} \Rightarrow 1 = \frac{{{x_0}^2}}{{{a^2}}} - \frac{{{y_0}^2}}{{{b^2}}} \le \frac{{{x_0}^2}}{{{a^2}}}\\ \Leftrightarrow {x_0}^2 \ge {a^2}\\ \Leftrightarrow \left| {{x_0}} \right| \ge a\end{array}\)
Luyện tập 1 Cho hyperbol \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\). a) Tìm tiêu cự và độ dài các trục b) Tìm các đỉnh và các đường tiệm cận. Phương pháp giải: Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) Trong đó: + Tiêu cự: \(2c = 2\sqrt {{a^2} + {b^2}} \) + Độ dài trục thực, trục ảo: \(2a,2b\) + Hai đỉnh \({A_1}( - a;0),{A_2}(a;0)\) + Hai đường tiệm cận \(y = - \frac{b}{a}x\) và \(y = \frac{b}{a}x\) Lời giải chi tiết: Ta có hypebol: \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\) \( \Rightarrow a = 8,b = 6,c = \sqrt {{a^2} + {b^2}} = 10\) a) + Tiêu cự: \(2c = 20\) + Độ dài trục thực: \(2a = 16\); trục ảo \(2b = 12.\) b) + Hai đỉnh \({A_1}( - 8;0),{A_2}(8;0)\) + Hai đường tiệm cận \(y = - \frac{3}{4}x\) và \(y = \frac{3}{4}x\)
|