Giải mục 1 trang 82, 83, 84 SGK Toán 8 tập 1– Chân trời sáng tạo

HĐ 1

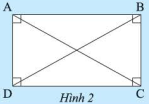
Dùng thước đo góc để đo số đo các góc $\widehat {\rm{A}}$, $\widehat {\rm{B}}$, $\widehat {\rm{C}}$, $\widehat {\rm{D}}$ ở Hình 1 và rút ra nhận xét và số đo của chúng.

Phương pháp giải:

Dùng thước đo góc để đo số đo 4 góc của tứ giác rồi rút ra nhận xét.

Lời giải chi tiết:

Sau khi đo, ta thấy bốn góc $\widehat {\rm{A}}$, $\widehat {\rm{B}}$, $\widehat {\rm{C}}$, $\widehat {\rm{D}}$ có số đo bằng nhau và bằng $90^\circ$

HĐ 2

Cho $ABCD$ là hình chữ nhật.

a) Chứng minh $AB$ // $CD$ và $AD$ // $BC$

b) Tam giác $ABD$ và tam giác $BAC$ có bằng nhau không? Vì sao?

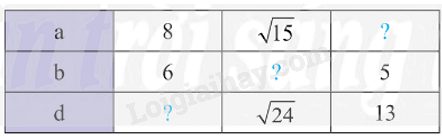
Phương pháp giải:

Áp dụng các tính chất của hình chữ nhật (cạnh, góc)

Lời giải chi tiết:

a) Vì $ABCD$ là hình chữ nhật (gt)

Suy ra $AB = CD$; $AD = BC$, $\widehat {DAB} = \widehat {ABC} = \widehat {DCB} = \widehat {ADC} = 90^\circ$

Xét $\Delta ABC$ và $\Delta CDA$ ta có:

$AB = CD$ (gt)

$\widehat {{\rm{ABC}}} = \widehat {{\rm{ADC}}}$ (cmt)

$BC = AD$ (gt)

Suy ra $\Delta ABC = \Delta CDA$ (c-g-c)

Suy ra $\widehat {{\rm{BAC}}} = \widehat {{\rm{ACD}}}$ và $\widehat {{\rm{ACB}}} = \widehat {{\rm{CAD}}}$ (hai cạnh tương ứng)

Mà hai góc ở vị trí so le trong

Suy ra $AB$ // $CD$; $BC$ // $AD$

b) Xét $\Delta ABD$ và $\Delta BAC$ ta có:

$AB$ chung

$\widehat {{\rm{BAD}}} = \widehat {{\rm{ABC}}}$ (cmt)

$AD = BC$ (cmt)

Suy ra $\Delta ABD = \Delta BAC$ (c-g-c)

TH 1

Cho biết $a$, $b$, $d$ lần lượt là độ dài các cạnh và đường chéo của một hình chữ nhật. Thay dấu ? trong bảng sau bằng giá trị thích hợp.

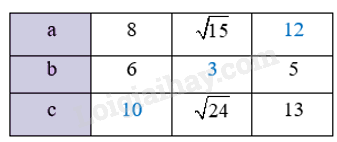
Phương pháp giải:

Áp dụng định lý Pythagore trong tam giác vuông

Lời giải chi tiết:

Giả sử $ABCD$ là hình chữ nhật ; $a$, $b$, $d$ lần lượt là độ dài của $AB$, $BC$, $AC$

Áp dụng định lý Pythagore vào $\Delta ABC$ vuông tại $B$ ta có:

$A{C^2} = A{B^2} + B{C^2}$

Do đó ${d^2} = {a^2} + {b^2}$ ; ${b^2} = {d^2} - {a^2}$; ${a^2} = {d^2} - {b^2}$

Suy ra: $d = \sqrt {{a^2} + {b^2}}$; $b = \sqrt {{d^2} - {a^2}}$; $a = \sqrt {{d^2} - {b^2}}$

Với $a = 8$; $b = 6$ ta có: $d = \sqrt {{8^2} + {6^2}}  = \sqrt {64 + 36}  = \sqrt {100}  = 10$

Với $a = \sqrt {15}$; $d = \sqrt {24}$ ta có:  $b = \sqrt {{{\sqrt {24} }^2} - {{\sqrt {15} }^2}}  = \sqrt {24 - 15}  = \sqrt 9  = 3$

Với $b = 5$; $d = 13$ ta có: $a = \sqrt {{{13}^2} - {5^2}}  = \sqrt {169 - 25}  = \sqrt {144}  = 12$

VD 1

Tìm bốn ví dụ về hình chữ nhật trong thực tế

Phương pháp giải:

Áp dụng định nghĩa hình chữ nhật và ứng dụng vào thực tiễn tìm các ví dụ về hình chữ nhật

Lời giải chi tiết:

Các ví dụ về hình chữ nhật trong thực tế: Mặt bảng; ti vi; mặt bàn; khung ảnh

HĐ 3

Cho hình bình hành $ABCD$ có $O$ là giao điểm của hai đường chéo. Giải thích các khẳng định sau:

a) Nếu $\widehat {{\rm{BAD}}}$ là góc vuông thì $\widehat {{\rm{ADC}}}$ và $\widehat {{\rm{ABC}}}$ cũng là góc vuông.

b) Nếu $AC = BD$ thì $\widehat {{\rm{BAD}}}$ vuông.

Phương pháp giải:

Áp dụng tính chất của hình bình hành

Lời giải chi tiết:

a) Vì $ABCD$ là hình bình hành (gt)

Suy ra $O$ là trung điểm của $AC$, $BD$

$AB = CD$; $AD = BC$; $AB$ // $CD$; $AD$ // $BC$

Nếu $\widehat {{\rm{BAD}}} = 90^\circ$ suy ra $AB \bot AD$

Mà $AB$ // $CD$; $AD$ // $BC$

Suy ra $AD \bot CD;\;AB \bot BC$

Suy ra $\widehat {ADC} = \widehat {ABC} = 90^\circ$

b) Xét $\Delta BAD$ và $\Delta CDA$ ta có:

$BA = CD$ (gt)

$AD$ chung

$BD = AC$ (gt)

Suy ra $\Delta BAD = \Delta CDA$ (c-c-c)

Suy ra $\widehat {{\rm{BAD}}} = \widehat {{\rm{CDA}}}$ (hai góc tương ứng)

Mà  $\widehat {BAD} + \widehat {CDA} = 180^\circ$(do $AB$ // $CD$ , cặp góc trong cùng phía)

Suy ra $\widehat {BAD} = \widehat {CDA} = 90^\circ$

TH 2

Chỉ được sử dụng compa, hãy kiểm tra tứ giác có phải là hình chữ nhật hay không.

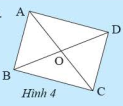
Phương pháp giải:

Sử dụng compa đo độ dài các cạnh, đường chéo

Lời giải chi tiết:

Gọi tứ giác trong hình là $ABCD$

Sử dụng compa đo độ dài ta thu được $AB = CD$; $AD = BC$; $AC = BD$

Tứ giác $ABCD$ ta có $AB = CD$; $AD = BC$ nên là hình bình hành

Hình bình hành $ABCD$ có hai đường chéo $AC = BD$ nên là hình chữ nhật

VD 2

a) Hãy sử dụng ê ke sao cho chỉ sau ba lần đo ta có thể xác định khung cửa sổ ở Hình 7 có phải là hình chữ nhật hay không?

b) Hãy sử dụng một cuộn dây, xác định khung cửa sổ trong Hình 7 có là hình chữ nhật hay không?

Phương pháp giải:

a) Sử dụng ê ke đo 3 góc của tứ giác rồi tinh góc còn lại

b) Đo độ dài các cạnh, đường chéo

Lời giải chi tiết:

a) Sử dụng ê ke, ta thấy khung cửa có 3 góc vuông

Áp dụng tính chất tổng 4 góc trong tứ giác, suy ra góc còn lại cũng là góc vuông

Vậy khung cửa là hình chữ nhật

b) 

Sử dụng thước dây:

- Đo độ dài đoạn thẳng $AB$ và đánh dấu 2 điểm trên đoạn dây (trùng với điểm $A$, $B$)

- Đặt một đầu đánh dấu trùng với điểm $C$ và kiểm tra thấy điểm đánh dấu còn lại trùng với $D$.

Vậy $AB = CD$

Thực hành tương tự ta có $AD = BC$; $AC = BD$

Tứ giác $ABCD$ có $AB = CD$; $AD = BC$ nên là hình bình hành

Mà $AC = BD$ nên $ABCD$ là hình chữ nhật

Vậy khung cửa có dạng hình chữ nhật