Giải mục 2 trang 17, 18 SGK Toán 12 tập 1 - Cùng khám phá

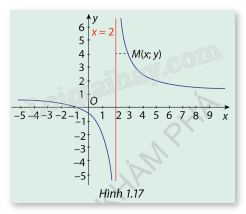
HĐ2

Trả lời câu hỏi Hoạt động 2 trang 17 SGK Toán 12 Cùng khám phá

Cho hàm số $y = \frac{{x + 1}}{{x - 2}}$có đồ thị (C ) như Hình 1.17.

a) Nêu nhận xét về khoảng cách từ điểm $M(x;y) \in (C)$đến đường thảng x=2 khi $x \to 2$ 

b) Tính các giới hạn $\mathop {\lim }\limits_{x \to {2^ + }} f(x)$ và $\mathop {\lim }\limits_{x \to {2^ - }} f(x)$

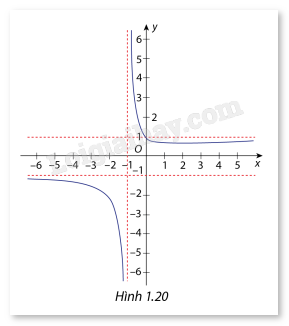
Phương pháp giải:

a) Nhìn đồ thị hàm số rồi nhận xét

b) Phân tích, rồi tính $\mathop {\lim }\limits_{x \to {2^ + }} f(x)$ và $\mathop {\lim }\limits_{x \to {2^ - }} f(x)$

Lời giải chi tiết:

a) Dựa vào đồ thị hàm số ta thấy:

Khi và thì khoảng cách giữa đồ thị (C) với đường thẳng x = 2 càng nhỏ

b) Ta có $f\left( x \right)\; = \frac{{x + 1}}{{x - 2}} = 1 + \frac{3}{{x - 2}} =  + \infty \;\;$

             $f\left( x \right)\; = \frac{{x + 1}}{{x - 2}} = 1 + \frac{3}{{x - 2}} =  - \infty \;\;$

LT2

Trả lời câu hỏi Luyện tập 2 trang 18 SGK Toán 12 Cùng khám phá

Cho hàm số $y = f(x) = \frac{{\sqrt {{x^2} + 1} }}{{x + 1}}$ có đồ thị là đường cong như hình 1.20. Hãy xác nhận các đường tiệm cận đứng và đường tiệm cận ngang của hàm số đã cho.

Phương pháp giải:

Xét $f(x).$

Lời giải chi tiết:

Ta có $\mathop {\lim }\limits_{x \to  - {1^ - }} f\left( x \right)\;$=$\mathop {\lim }\limits_{x \to  - {1^ - }} \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} =  - \infty \;$, $\mathop {\lim }\limits_{x \to  - {1^ + }} f\left( x \right)\;$=$\mathop {\lim }\limits_{x \to  - {1^ + }} \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} =  + \infty \;$

Suy ra x = - 1 là đường tiệm cận đứng của hàm số.

Ta có $\mathop {\lim }\limits_{x \to  + \infty } f(x)\; = \mathop {\lim }\limits_{x \to  + \infty } \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = \mathop {\lim }\limits_{x \to \infty } \frac{{\sqrt {1 + \frac{1}{{{x^2}}}} }}{{1 + \frac{1}{x}}} = 1\;\;$, $\mathop {\lim }\limits_{x \to  - \infty } f(x)\; = \mathop {\lim }\limits_{x \to  - \infty } \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = \mathop {\lim }\limits_{x \to  - \infty } \frac{{\sqrt {1 + \frac{1}{{{x^2}}}} }}{{1 + \frac{1}{x}}} = 1\;\;$

Suy ra y = 1 là đường tiệm cận ngang của hàm số.