Giải mục 2 trang 21, 22 Chuyên đề học tập Toán 11 - Chân trời sáng tạoGiả sử ĐO là phép đối xứng tâm O. Lấy hai điểm tùy ý A, B sao cho ba điểm O, A, B không thẳng hàng.
Lựa chọn câu để xem lời giải nhanh hơn
Khám phá 2 Giả sử ĐO là phép đối xứng tâm O. Lấy hai điểm tùy ý A, B sao cho ba điểm O, A, B không thẳng hàng. Gọi A’, B’ lần lượt là ảnh của A, B qua ĐO. So sánh tam giác OAB và tam giác O’A’B’ rồi so sánh A’B’ và AB. Phương pháp giải: Vẽ hình sau đó quan sát và so sánh Lời giải chi tiết:
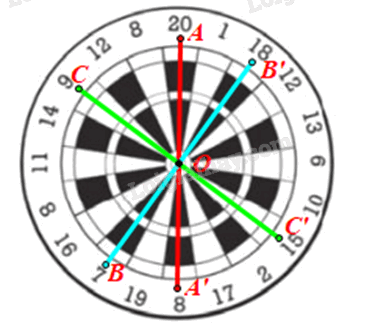
Theo đề, ta có \({Đ_O}\left( A \right){\rm{ }} = {\rm{ }}A'.\) Suy ra O là trung điểm AA’, do đó \(OA{\rm{ }} = {\rm{ }}OA'.\) Chứng minh tương tự, ta được \(OB{\rm{ }} = {\rm{ }}OB'.\) Xét \(\Delta OAB\) và \(\Delta OA'B'\), có: \(OA{\rm{ }} = {\rm{ }}OA'\) (chứng minh trên); \(\widehat {AOB} = \widehat {A'OB'}\) (đối đỉnh); \(OB{\rm{ }} = {\rm{ }}OB'\) (chứng minh trên). Do đó \(\Delta OAB{\rm{ }} = {\rm{ }}\Delta OA'B'{\rm{ }}\left( {c.g.c} \right).\) Suy ra \(A'B'{\rm{ }} = {\rm{ }}AB\) (cặp cạnh tương ứng). Vậy \(\Delta OAB{\rm{ }} = {\rm{ }}\Delta OA'B'{\rm{ }}\) và \(A'B'{\rm{ }} = {\rm{ }}AB.\) Thực hành 2 Trong mặt phẳng tọa độ Oxy, tìm ảnh qua ĐO của a) điểm M(3; –4); b) đường thẳng d: x – 3y + 6 = 0; c) đường tròn (C): (x + 2)2 + (y – 1)2 = 4. Phương pháp giải: Nếu \(M'{\rm{ }} = {\rm{ }}{Đ_I}\left( M \right)\) thì \(\left\{ \begin{array}{l}{x_{M'}} + {x_M} = 2{x_I}\\{y_{M'}} + {y_M} = 2{y_I}\end{array} \right.\) (I là trung điểm của MM’) Lời giải chi tiết: a) Gọi M’ là ảnh của M qua ĐO. Suy ra O là trung điểm của MM’ với \(M\left( {3;{\rm{ }}-4} \right).\) Do đó \(\left\{ \begin{array}{l}{x_{M'}} = 2{x_O} - {x_M} = 2.0 - 3 = - 3\\{y_{M'}} = 2{y_O} - {y_M} = 2.0 + 4 = 4\end{array} \right.\) Vậy \(M'\left( {-3;{\rm{ }}4} \right).\) b) • Chọn \(A\left( {0;{\rm{ }}2} \right) \in d:{\rm{ }}x{\rm{ }}-{\rm{ }}3y{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}0.\) Gọi A’là ảnh của A qua \({Đ_O}.\) Suy ra O là trung điểm của AA’ với A(0; 2) Do đó \(\left\{ \begin{array}{l}{x_{A'}} = 2{x_O} - {x_A} = 2.0 - 0 = 0\\{y_{A'}} = 2{y_O} - {y_A} = 2.0 - 2 = - 2\end{array} \right.\) Vì vậy A’(0; –2). • Đường thẳng \(d:{\rm{ }}x{\rm{ }}-{\rm{ }}3y{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}0\) có vectơ pháp tuyến \({\rm{\vec n}} = \left( {1; - 3} \right)\) Gọi d’ là ảnh của d qua \({Đ_O}.\) Suy ra d’ song song hoặc trùng với d, nên d’ nhận vectơ pháp tuyến của d là \({\rm{\vec n}} = \left( {1; - 3} \right)\) làm vectơ pháp tuyến. Vậy đường thẳng d’ đi qua A’(0; –2) và nhận làm vectơ \({\rm{\vec n}} = \left( {1; - 3} \right)\) pháp tuyến nên có phương trình là: \(1\left( {x{\rm{ }}-{\rm{ }}0} \right){\rm{ }}-{\rm{ }}3\left( {y{\rm{ }} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow x-3y-6 = 0.\) c) Đường tròn \(\left( C \right):{\rm{ }}{\left( {x{\rm{ }} + {\rm{ }}2} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}1} \right)^2}\; = {\rm{ }}4\) có tâm I(–2; 1), bán kính R = 2. Gọi (C’) là ảnh của (C) qua ĐO nên (C’) có tâm là ảnh của I(–2; 1) và có bán kính R’ = R = 2. Gọi I’= ĐO(I). Suy ra O là trung điểm \(II'.\) Do đó \(\left\{ \begin{array}{l}{x_{I'}} = 2{x_O} - {x_I} = 2.0 + 2 = 2\\{y_{I'}} = 2{y_O} - {y_I} = 2.0 - 1 = - 1\end{array} \right.\) Vì vậy tọa độ I’(2; –1). Vậy đường tròn (C’) là ảnh của (C) qua ĐO, có tâm I’(2; –1) và R’ = 2 nên có phương trình là: \({\left( {x{\rm{ }}-{\rm{ }}2} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }} + {\rm{ }}1} \right)^2}\; = {\rm{ }}4.\) Vận dụng 2 Trong Hình 6, tìm các số ghi tại điểm đối xứng qua tâm bia với điểm ghi các số 20; 7; 9.
Phương pháp giải: Quan sát hình 6 để tìm Lời giải chi tiết:
Gọi O là tâm bia. • Lấy điểm A nằm trong ô có điểm ghi số 20. Lấy A’ đối xứng với A qua O. Khi đó ta được điểm A’ nằm trong ô có điểm ghi số 8. • Lấy điểm B nằm trong ô có điểm ghi số 7. Lấy B’ đối xứng với B qua O. Khi đó ta được điểm B’ nằm trong ô có điểm ghi số 18. • Lấy điểm C nằm trong ô có điểm ghi số 9. Lấy C’ đối xứng với C qua O. Khi đó ta được điểm C’ nằm trong ô có điểm ghi số 15. Vậy điểm đối xứng qua tâm bia với điểm ghi các số 20; 7; 9 lần lượt là 8; 18; 15.
|