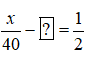Giải mục 2 trang 38, 39 SGK Toán 8 tập 2 – Chân trời sáng tạoThay dấu bằng các dữ liệu thích hợp để hoàn thành lời giải bài toán. Một người đi xe gắn máy từ A đến B với tốc độ (40km/h). Lúc về người đó đi với tốc độ (50km/h) nên thời gian về ít hơn thời gian đi là (30) phút. Tìm chiều dài quãng đường AB.
Lựa chọn câu để xem lời giải nhanh hơn
HĐ2 Video hướng dẫn giải Thay dấu ? bằng các dữ liệu thích hợp để hoàn thành lời giải bài toán. Một người đi xe gắn máy từ A đến B với tốc độ \(40km/h\). Lúc về người đó đi với tốc độ \(50km/h\) nên thời gian về ít hơn thời gian đi là \(30\) phút. Tìm chiều dài quãng đường AB. Giải Gọi chiều dài quãng đường AB là \(x\left( {km} \right)\). Điều kiện ? Thời gian đi là: \(\dfrac{x}{{40}}\) giờ. Thời gian về là: ? giờ Ta có: 30 phút = \(\dfrac{1}{2}\) giờ. Vì thời gian về ít hơn thời gian đi là \(\dfrac{1}{2}\) giờ nên ta có phương trình: Giải phương trình, ta được x=? thỏa mãn điều kiện x> ? Vậy chiều dài quãng đường AB là ?. Phương pháp giải: Quãng đường đi là một đại lượng dương. Ta có công thức biểu diễn quãng đường, vận tốc, thời gian như sau: \(s = vt\) với \(s\) là quãng đường; \(v\) là vận tốc; \(t\) là thời gian. Lời giải chi tiết:
TH2 Video hướng dẫn giải Một người mua 36 bông hoa hồng và bông hoa cẩm chướng hết tất cả 136 800 đồng. Giá mỗi bông hoa hồng là 3 000 đồng, giá mỗi bông hoa cẩm chướng là 4 800 đồng. Tính số bông hoa mỗi loại.
Phương pháp giải: Giải bài toán bằng cách lập phương trình ta thực hiện 3 bước sau: Bước 1: Lập phương trình - Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số. - Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết. - Lập phương trình biểu diễn mối quan hệ giữa các đại lượng. Bước 2: Giải phương trình. Bước 3: Trả lời - Kiểm tra xem trong các nghiệm của phương trình , nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không. - Kết luận. Lời giải chi tiết: Gọi số bông hoa hồng đã mua là \(x\) (bông). Điều kiện: \(x \in {\mathbb{N}^*};x \le 36\) Vì tổng số hoa người đó đã mua là 36 bông nên số bông hoa cẩm chướng người đó đã mua là: \(36 - x\)(bông). Vì một bông hoa hồng có giá là 3 000 đồng nên số tiền mua hoa hồng là \(3000x\) đồng. Vì một bông hoa cẩm chướng có giá là 4 800 đồng nên số tiền mua hoa cẩm chướng là \(\left( {36 - x} \right).4800\) (đồng). Vì tổng số tiền mua 2 loại hoa là 136 800 đồng nên ta có phương trình: \(3000x + \left( {36 - x} \right).4800 = 136800\) \(3000x + 172800 - 4800x = 136800\) \(3000x - 4800x = 136800 - 172800\) \( - 1800x = - 3600\) \(x = \left( { - 36000} \right):\left( { - 1800} \right)\) \(x = 20\) (thỏa mãn điều kiện) Vậy số bông hoa hồng đã mua là 20 bông; Số bông hoa cẩm chướng đã mua là \(36 - 20 = 16\) bông. VD Video hướng dẫn giải Giải bài toán đã cho trong câu hỏi khởi động (trang 37) Phương pháp giải: Giải bài toán bằng cách lập phương trình ta thực hiện 3 bước sau: Bước 1: Lập phương trình - Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số. - Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết. - Lập phương trình biểu diễn mối quan hệ giữa các đại lượng. Bước 2: Giải phương trình. Bước 3: Trả lời - Kiểm tra xem trong các nghiệm của phương trình , nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không. - Kết luận. Lời giải chi tiết: Gọi giá tiền đôi giày lúc chưa giảm giá là \(x\) (đồng). Điều kiện: \(x > 0\). Sau khi giảm giá \(15\% \) thì giá mới của đôi giày bằng \(85\% \) giá ban đầu của đôi giày. Ta có phương trình: \(x.85\% = 1275000\) \(x = 1275000:85\% \) \(x = 1500000\) (thỏa mãn) Vậy giá của đôi giày khi chưa giảm giá là 1 500 000 đồng.
|