Giải mục 3 trang 70, 71 SGK Toán 8 – Chân trời sáng tạo

HĐ 3

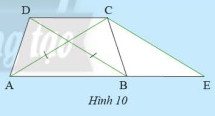
Cho hình thang $ABCD$ có hai đáy là $AB$, $CD$ và có hai đường chéo bằng nhau (Hình 10). Vẽ đường thẳng đi qua $C$, song song với $BD$ và cắt $AB$ tại $E$.

a) Tam giác $CAE$ là tam giác gì? Vì sao?

b) So sánh tam giác $ABD$ và tam giác $BAC$

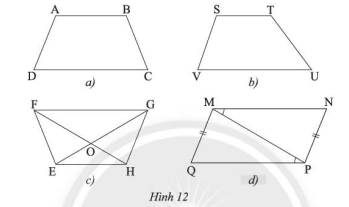
Phương pháp giải:

Sử dụng tính chất của hình thang cân chứng minh $\Delta CAE$ cân; $\Delta ABD = \Delta BAC$

Lời giải chi tiết:

a) Vì $ABCD$ là hình thang cân (gt)

$\Rightarrow AC = BD$ và $AB\;{\rm{//}}\;CD$

Xét $\Delta BCD$ và $\Delta CBE$ ta có:

$\widehat {DCB} = \widehat {CBE}$ (do $AB$ // $CD$)

$BC$ chung

$\widehat {CBD} = \widehat {BCE}$ (do  $CE$ // $BD$)

Suy ra $\Delta BCD = \Delta CBE$ (g-c-g)

Suy ra $BD = CE$ (hai cạnh tương ứng)

Mà $AC = BD$ (cmt)

Suy ra $AC = EC$

Suy ra $\Delta CAE$ cân tại $C$

b) Xét $\Delta ABD$ và $\Delta BAC$ ta có:

$DA = BC$ (do $ABCD$ là hình thang cân)

$\widehat {DAB} = \widehat {CBA}$ (Do $ABCD$ là hình thang cân)

$AB$ chung

Suy ra $\Delta ABD = \Delta BAC$ (c-g-c)

TH 3

Sử dụng thước đo góc và thước đo độ dài để tìm hình thang cân trong các tứ giác ở Hình 12.

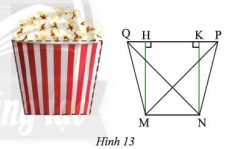
Phương pháp giải:

Sử dụng thước đo góc và đo độ dài và dấu hiệu nhận biết để tìm hình thang cân

Lời giải chi tiết:

Sau khi đo độ dài các cạnh và các góc, ta thấy $ABCD$, $EFGH$ là các hình thang cân.

VD 4

Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân $MNPQ$ (Hình 13) với hai đáy $MN = 6cm$, $PQ = 10$cm và độ dài hai đường chéo $MN = NQ = 8\sqrt 2$ cm. Tính độ dài đường chéo và cạnh bên của hình thang  

Phương pháp giải:

Chứng minh $QH = KP$

Tính độ dài các đoạn thẳng $HK$, $QH$, $KP$

Áp dụng định lý Pythagore tính độ dài $MH$, $MQ$

Lời giải chi tiết:

a) Xét $\Delta MHQ$ và $\Delta NKP$ ta có:

$\widehat {MHQ} = \widehat {NKP} = 90^\circ$

$MQ = NP$ (do $MNPQ$ là hình thang cân)

$\widehat {MQP} = \widehat {NPQ}$ (do $MNPQ$ là hình thang cân)

Suy ra: $\Delta MHQ = \Delta NKP$ (ch – gn)

Suy ra: $HQ = KP$ (hai cạnh tương ứng)

Suy ra $HQ = KP = \frac{{PQ - HK}}{2} = \frac{{10 - 6}}{2} = 2$ (cm)

$HP = 8$cm

Áp dụng định lý Pythagore vào tam giác vuông $MHP$ ta có:

$M{H^2} = M{P^2} - H{P^2} = {\left( {8\sqrt 2 } \right)^2} - {8^2} = 128 - 64 = 64$

$MH = 8$ (cm)

Áp dụng định lý Pythagore vào tam giác vuông $MHQ$ ta có:

$M{Q^2} = M{H^2} + Q{H^2} = {8^2} + {2^2} = 68$

$MQ = \sqrt {68}$ (cm)