Giải mục 3 trang 72 SGK Toán 9 tập 2 - Chân trời sáng tạoa) Gọi O là giao điểm của hai đường chéo AC và BD. So sánh độ dài các đoạn thẳng OA, OB, OC, OD. Nêu nhận xét về tâm và đường kính của đường tròn ngoại tiếp hình chữ nhật ABCD. b) Xác định tâm và bán kính của đường tròn ngoại tiếp hình vuông MNPQ có cạnh bằng a.
Lựa chọn câu để xem lời giải nhanh hơn
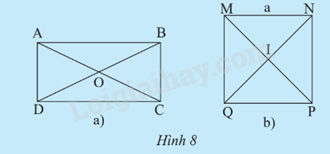
HĐ3 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 3 trang 72 SGK Toán 9 Chân trời sáng tạo a) Gọi O là giao điểm của hai đường chéo AC và BD. So sánh độ dài các đoạn thẳng OA, OB, OC, OD. Nêu nhận xét về tâm và đường kính của đường tròn ngoại tiếp hình chữ nhật ABCD. b) Xác định tâm và bán kính của đường tròn ngoại tiếp hình vuông MNPQ có cạnh bằng a.
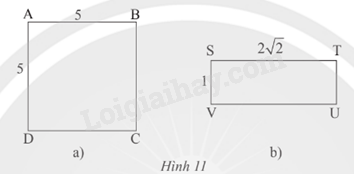
Phương pháp giải: Dựa vào: Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường. Lời giải chi tiết: a) Độ dài các đoạn thẳng OA, OB, OC, OD là bằng nhau. Nhận xét: + Tâm của đường tròn ngoại tiếp hình chữ nhật ABCD là giao điểm của hai đường chéo. + Đường kính của đường tròn ngoại tiếp hình chữ nhật ABCD là đường chéo của hình chữ nhật. b) Tâm của đường tròn ngoại tiếp hình vuông MNPQ là I. Bán kính của đường tròn ngoại tiếp hình vuông MNPQ bằng một nửa cạnh huyền. Đường chéo của hình vuông là: \(\sqrt {a^2 + a^2} = a\sqrt 2\) Bán kính của đường tròn ngoại tiếp hình vuông MNPQ là: R = IM = IN = IP = IQ = \(\frac{{{a\sqrt 2}}}{2}\). TH3 Video hướng dẫn giải Trả lời câu hỏi Thực hành 3 trang 73 SGK Toán 9 Chân trời sáng tạo Xác định tâm và bán kính của đường tròn ngoại tiếp hình vuông và hình chữ nhật trong Hình 11.
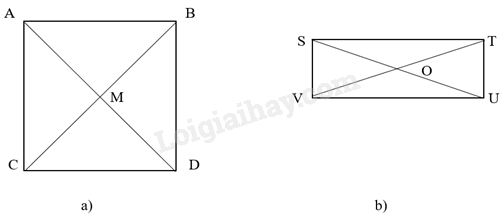
Phương pháp giải: Dựa vào: Đường tròn ngoại tiếp hình chữ nhật, hình vuông có tâm là giao điểm của hai đường chéo và có bán kính bằng nửa đường chéo. Lời giải chi tiết:
a) Hình vuông ABCD có M là giao điểm của hai đường chéo. Suy ra đường tròn ngoại tiếp hình vuông ABCD có tâm M và bán kính R = \(\frac{{a\sqrt 2 }}{2} = \frac{{5\sqrt 2 }}{2}\). b) Hình chữ nhật STUV có O là giao điểm của hai đường chéo. Suy ra đường tròn ngoại tiếp hình chữ nhật STUV có tâm O và bán kính R = \(\frac{{SU}}{2} = \frac{{\sqrt {S{T^2} + U{T^2}} }}{2} = \frac{{\sqrt {{{\left( {2\sqrt 2 } \right)}^2} + {1^2}} }}{2} = \frac{{\sqrt 9 }}{2} = \frac{3}{2}\). VD3 Video hướng dẫn giải Trả lời câu hỏi Vận dụng 3 trang 73 SGK Toán 9 Chân trời sáng tạo Một người muốn thiết kế một bảng hiệu gồm một hình vuông nội tiếp một đường tròn bán kính R = 3 cm (Hình 12). Tính diện tích hình vuông đó.
Phương pháp giải: Dựa vào: Đường tròn ngoại tiếp hình chữ nhật, hình vuông có tâm là giao điểm của hai đường chéo và có bán kính bằng nửa đường chéo. Lời giải chi tiết: Ta thấy đường tròn ngoại tiếp hình vuông suy ra độ dài đường chéo hình vuông là đường kính của hình tròn. Độ dài của đường chéo hình vuông là: d = 2.R = 2.3 = 6 cm. Độ dài cạnh hình vuông là: a = \(\sqrt {\frac{{{d^2}}}{2}} = \sqrt {\frac{{{6^2}}}{2}} = 3\sqrt 2 \) cm. Diện tích hình vuông là: \(3\sqrt 2 .3\sqrt 2 \) = 18 (cm2).
|